
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Мы получили замечательный результат.
Тема. Первообразная функция
Занятие 3.
На прошлом занятии мы рассматривали дифференциал функции
 (1.3)
(1.3)
Напомним, что переменная  и величина
и величина  не зависят друг от друга и задаются произвольно. Была доказана теорема
не зависят друг от друга и задаются произвольно. Была доказана теорема
Теорема 1.1. Вид формулы дифференциала функции не изменится, если аргумент функции заменить новой переменной.
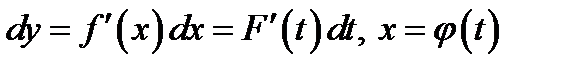 . (1.7)
. (1.7)
Таким образом формула дифференциала 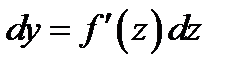 справедлива независимо от того является ли переменное
справедлива независимо от того является ли переменное  независимым или оно есть функция другого независимого переменного.
независимым или оно есть функция другого независимого переменного.
Хорошо известно, что для всякой математической операции существует обратная к ней операция. Например, по заданной функции можно легко вычислить её дифференциал. На прошлом занятии мы решали и обратную задачу, а именно, находили функцию по заданному её дифференциалу.
Определение 3.1. Будем считать вычисление производной 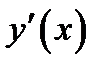 или дифференциала
или дифференциала  ,по заданной на интервале
,по заданной на интервале 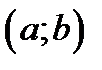 функции
функции  ,операцией прямого действия.
,операцией прямого действия.
Обратной к этой операции является операция вычисления на интервале 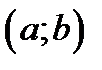 функции
функции  если на
если на 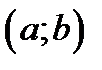 задана производная этой функции
задана производная этой функции 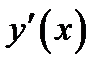 или её дифференциал
или её дифференциал  .
.
Нахождение функции по её производной или дифференциалу является одной из важнейших задач математического анализа.
Определение 3.2. Функция 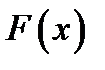 называется первообразной функцией по отношению к заданной функции
называется первообразной функцией по отношению к заданной функции  , если выполнены два условия:
, если выполнены два условия:
1)  определены на одном интервале
определены на одном интервале 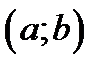 ;
;
2)  .
.
В математическом анализе доказан фундаментальный факт.
Теорема 3.1. Длялюбой непрерывной на интервале  функции
функции 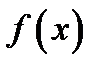
существует на том же интервале первообразная функция  .
.
Однако не всякую первообразную можно выразить конечной формулой через элементарные функции. Например, у элементарных функций:  по теореме 3.1 первообразная имеется, но не является элементарной функцией.
по теореме 3.1 первообразная имеется, но не является элементарной функцией.
Замечание. Если  является первообразной функцией для непрерывной функции
является первообразной функцией для непрерывной функции 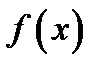 ,
, 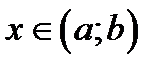 , то
, то

также является первообразной для функции 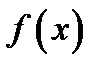 ,
, 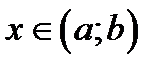 .
.
Теорема 3.2. Если две функции 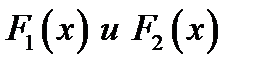 ,
, 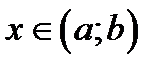 являются первообразными к одной и той же функции
являются первообразными к одной и той же функции  , то
, то  . Здесь
. Здесь  -произвольная постоянная.
-произвольная постоянная.
Доказательство. Обозначим разность  . По условию теоремы
. По условию теоремы 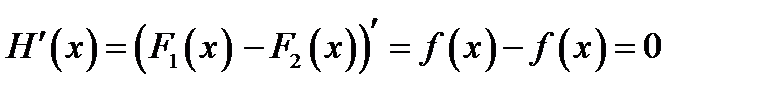 ,
, 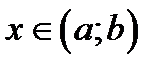 . Рассмотрим два любых числа
. Рассмотрим два любых числа  из интервала
из интервала 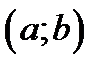 . И пусть для определённости
. И пусть для определённости  Применим к функции
Применим к функции  на отрезке
на отрезке  теорему Лагранжа
теорему Лагранжа 
Теорема 3.2. доказана.
Операцию нахождения первообразной называют неопределённым
интегрированием. Неопределённый интегралобозначают математическим символом 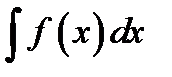 , в котором знак
, в котором знак  называют интегралом, функцию
называют интегралом, функцию 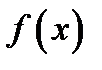 - подынтегральной функцией, дифференциальное выражение
- подынтегральной функцией, дифференциальное выражение  - подынтегральным выражением, а переменную
- подынтегральным выражением, а переменную  - переменной интегрирования.
- переменной интегрирования.
Из теоремы 3.2. и определения первообразной следует, что если функция  на интервале
на интервале 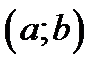 является первообразной для функции
является первообразной для функции 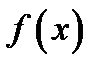 ,то
,то
 (3.1)
(3.1)
Замечание. Если справедлива формула (3.1),то справедливы и равенства
 (3.2)
(3.2)
Используя первообразную, можно вычислять площади плоских фигур, границы которых не являются отрезками прямых линий.
| Y |
 , ограниченную графиком непрерывной функции
, ограниченную графиком непрерывной функции  , отрезками прямых
, отрезками прямых  и отрезком оси
и отрезком оси  .
.
| Q |
| F |
| A |
| D |
| E |
| N |
| X |
| P |
| M |
| C |
| B |
| O |
| a |
| b |
| x+dxxx |
| x |
Обозначим площадь переменной трапеции  через
через  , площадь трапеции
, площадь трапеции  через
через  . Тогда площадь трапеции
. Тогда площадь трапеции  будет равна
будет равна  . Площадь прямоугольника
. Площадь прямоугольника  меньше площади трапеции
меньше площади трапеции  . А площадь прямоугольника
. А площадь прямоугольника  больше площади трапеции
больше площади трапеции  . Таким образом
. Таким образом 
Разделив полученное неравенство на  , получаем
, получаем

Переходя к пределу в этом неравенстве, получаем

Откуда  и следовательно
и следовательно  .
.
Согласно теореме 3.2 площадь  , где
, где  есть некоторая первообразная
есть некоторая первообразная
к функции  . По построению
. По построению  . Поэтому
. Поэтому  .
.
Площадь всей трапеции 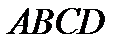
 (3.3)
(3.3)
Мы получили замечательный результат.
Площадь криволинейной трапеции, ограниченной графиком непрерывной функции  , отрезками прямых
, отрезками прямых  и отрезком оси
и отрезком оси  , равна разности значений первообразной функции
, равна разности значений первообразной функции 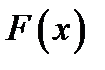 к функции
к функции  в конечной и начальной точках отрезка
в конечной и начальной точках отрезка 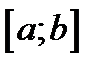 .
.
Упражнение. Используя результат примера 1, вычислите площади криволинейных
трапеций ограниченных линиями
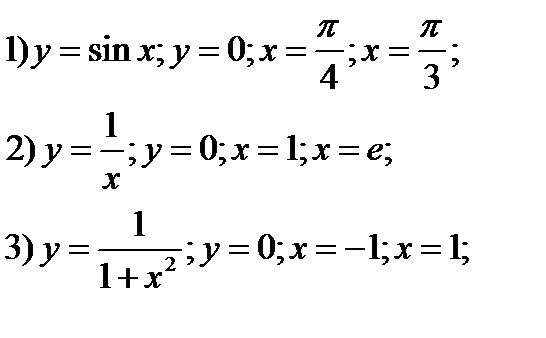
Ответы. 1)0,21; 2) 1; 3) 1,57;
Не нашли, что искали? Воспользуйтесь поиском: