Основные свойства неопределённого интегрирования

Свойство 1. Дифференциал от неопределённого интеграла равен подынтегральному выражению

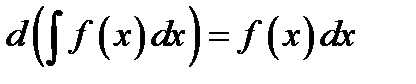(3.4)

Доказательство. Пусть . Тогда из формулы (3.1) и правила (1.4) имеем

Свойство 2. Интеграл от дифференциала функции 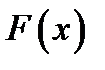равен сумме этой функции и произвольной постоянной

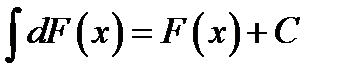(3.5)

Доказательство. Пусть тогда 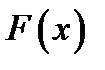является первообразной к функции (см. определение 3.2). Из формулы (3.1) следует доказательство.

Замечание. Формула (3.5) используется для вычисления неопределённых интегралов. Формула (3.4) используется для проверки полученного результата.

Не нашли, что искали? Воспользуйтесь поиском: