Невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому.

Невозможно создание вечного двигателя второго рода, т.е. машины, которая периодически при постоянной температуре превращает тепло среды в работу

Некоторые формулировки связаны понятием термодинамической функции энтропия (S), отражающей степень разупорядоченности системы.

Существует функция состояния – энтропия, приращение которой при обратимых процессах равно приведенному теплу; энтропия замкнутой системы стремится к максимуму и не может самопроизвольно уменьшаться

В формализованном виде эта формулировка выглядит следующим образом:

S≥Q/T

или для малых приращений

DS≥δQ/T

где:отношение Q/T называется приведенным теплом.

Соответственно, если система замкнута (Q/T=0):

DS≥0

Т.о. в изолированной (замкнутой) системе изменение энтропии служит критерием направления самопроизвольного процесса – процессы в этих системах идут только в направлении увеличения энтропии и в равновесии энтропия максимальна.

В неизолированных системах энтропия может, как увеличиваться, так и уменьшаться в зависимости от приведенного тепла, поэтому S не может служить критерием направления процессов в неизолированных системах.

Примеры. Пусть в одну половину закрытого, предварительно откачанного сосуда, разделенного перегородкой, введен кислород. Если удалить перегородку, то молекулы кислорода, двигающиеся во всех направлениях, рав­номерно распределяются по всему объему сосуда. Нельзя считать невозможным, что в какой-то момент все молекулы кислорода вновь соберутся в одной половине сосуда, а в другой установится вакуум. Однако ясно, что это тем менее вероятно, чем большее число молекул находится в сосуде.

Если учесть, что даже в одном кубическом миллиметре газа при нормальных условиях число молекул составляет приблизи­тельно 3×10¹⁶, то можно понять, что вероятность такого явления исчезающе мала. Наоборот, вероятность расширения газа в пу­стоту очень велика, и именно этим объясняется то, что указанный процесс носит односторонний характер.

В мешок с белым песком насыпем красный песок. После встря­хивания мешка, которое заменяет тепловое движение молекул, через короткое время песчинки обоих цветов равномерно переме­шаются. Очевидно, разделение образовавшейся смеси путем дальнейшего встряхивания практически невозможно. Из этого следует, что односторонность процессов может наблюдаться и в чисто механических системах, если число частиц в них доста­точно велико. Состояние, при котором песчинки перемешаны, более вероятно, так как оно может быть осуществлено большим числом способов, чем состояние, когда песчинки обоих цветов разделены.

Из приведенного примера видно, что каждое состояние может быть охарактеризовано определенной вероятностью. При этом равновесию отвечает наибольшая вероятность, и, следовательно, вероятность данного состояния является тем критерием, который определяет направление процесса и позволяет найти равновесие.

В изолированных системах энтропия может только увеличи­ваться и при равновесии достигать максимума. Поэтому ее можно использовать для суждения о направлении процессов в таких системах. Однако на практике большинство процессов протекает в неизолированных системах. Действие почти всех промышлен­ных агрегатов связано с теплообменом и изменениями объема. Поэтому для таких незамкнутых систем целесообразно выбрать другие критерии равновесия. Возможность или невозможность процессов при этом связывается с работой, которую они могут произвести. Так как работа зависит от пути процесса, то ее ве­личину, вообще говоря, нельзя выбрать в качестве критерия равновесия. Однако, если ограничить рассмотрение частным слу­чаем процесса при постоянной температуре, то оказывается, что максимальная работа при его обратимом протекании определяется изменением некоторой функции состояния.

Такими критериями являются другие термодинамические функции, энергия Гельмгольца (F) и свободная энергия Гиббса (G).

F=U-TS (соответственно ΔF=ΔU-TΔS)

G=H-TS (соответственно ΔG=ΔH-TΔS)

Из первого и второго закона термодинамики легко получить, что для систем с постоянным объемом и температурой справедливо выражение:

dF ≤ 0

а для систем с постоянным давлением и температурой

dG ≤ 0

Т.о. функция F в системах с постояннымиTиV в необратимых процессах может только убывать, а в обратимых процессах (или в состоянии равновесия) она минимальна (приращение равно нулю). В таких системах по изменению F можно судить о направлении движения системы.

Аналогично, свободная энергия Гиббса (или просто энергия Гиббса) является критерием, по которому можно судить о направлении движения процессов в системах с постоянными температурой и давлением. Последние системы наиболее распространенны в металлургии, поэтому энергия Гиббса наиболее часто используется в термодинамических расчетах в металлургии.

К следующему занятию принести копии таблиц
термодинамических данных из Казачкова

Тема 2. Расчеты равновесий в газовых системах(2 часа)

(для работы на практическом занятии необходимы таблицы термодинамических данных, например, из книги Казачков Е.А. Расчеты по теории металлургических процессов. - М.: Металлургия, 1988. - 288 с.)

В подавляющем большинстве металлургических процессов свойства газовой фазы близки к свойствам идеальных газов. Неподчинение законам идеальных газов наблюдается лишь при очень высоких давлениях либо при очень низких температурах. Поэтому, как правило, в металлургических расчетах поведение газовой фазы описывается с использованием законов для идеальных газов, один из которых (закон Клапейрона-Менделеева) мы уже упоминали на первом занятии.

В металлургических расчетах приходится иметь дело с газами, находящимися при небольших давлениях, поэто­му применение законов идеальных газов к реальным газам да­ет незначительную ошибку, которой можно в расчетах пренеб­речь.. Закон Бойля — Мариотта устанавли­вает связь между давлением и объемом газа: при постоянной температуре объемы данной массы газа обратно пропорцио­нальны давлениям.

V₁: V = P: P₁ или (PV)_t = (P₁V₁)_t = const,

т. е. произведение давления на объем, занимаемый одной и той же массой газа, при постоянной температуре есть величина по­стоянная.

Закон Гей-Люссака выражает зависи­мость объема и давления газа от температуры: при постоянном давлении объем данной массы газа при повышении температу­ры на 1° увеличивается на 1/273, или 0,00367 того объема, который та же масса газа занимает при 0° С. Прирост объема при повышении температуры на 1° называется термическим коэф­фициентом расширения и обозначается α.Отсюда приtгаз будет занимать объем:

V = V₀(1 + αt) = V₀αT;

Также следует, что объемы, занимаемые данной массой газа при постоянном давлении, относятся между собой, как их абсолютные темпера­туры.: (V₁/V₂) p = (T₁/T₂) p

Объединение законов Бойля—Мариотта и Гей-Люссака и сочетание их с законом Аво-гадро дает уравнение Менделеева—Клапейрона, связывающее все три параметра, характеризующие состояние газа.

pV= nRТ; pV= (G/M)RТ, G – масса газа,M –молекулярная масса

Из физической химии известно также, что для одного моля идеального газа энергия Гиббса равна:

где:p_i – парциальное давление газового компонента i (p_i=P_i/P_об, P_i – давление газа i, P_об. – общее давление газа), атм.; - стандартная энергии Гиббса газа i.

Как следует из уравнения стандартная энергии Гиббса газа i это энергия Гиббса газа, взятого при давлении 1 атм. (тогда ln в правой части будет равен нулю). зависит от температуры.

Как вам должно быть известно в равновесии в идеальных системах соотношение концентраций, записанное определенным образом остается постоянным при постоянстве температуры.

Закон действующих масс или закон Гульдберга и Вааге.

Возьмем реакцию с газовыми компонентами:

A_г + 3B_г=5D_г

Тогда выражениезакона действующих масс (или Гульдберга и Вааге):

где: - константа равновесия реакции, зависящая (для данной реакции) только от температуры p_i – парциальное давление газового компонента i.

Таким образом, парциальные давления реагирующих газов при равновесии связаны между собой определенным соотношением, которое является выражением закона действующих масс. При постоянной температуре это дробь, числитель которой есть про­изведение парциальных давлений веществ, образующихся при реакции, а знаменатель - произведение парциальных давлений исходных веществ. Показателями степеней при парциальных дав­лениях являются стехиометрические коэффициенты, в которых данные вещества вступают в реакцию. При равновесии такая дробь есть величина постоянная и называется константой равновесияКр.

Закон действующих масс был выведен Гульдбергом и Вааге из статистических соображений.Из уравнения видно, что величина Кр дает количе­ственную оценку равновесия. Если ее численное значение велико, то равновесие реакции сдвинуто в сторону образования продуктов реакции, если оно мало, то в смеси преобладают исходные вещества.

(Для идеальных газов законно действующих масс может быть записан и через концентрации: )

Гульдберг и Вааге вывели этот закон из статистических соображений, положив, что в равновесии скорости прямой и обратной реакций равны.

Для определения абсолютных величин парциальных давлений, кроме значения Кр, необходимо знать состав смеси до начала реакции. В этом случае знание константы равновесия позволяет рассчитать выход и состав равновесной смеси. Возможность подобных количественных расчетов показывает практическую важность закона действующих масс

Уравнение для закона действующих масс легко выводится из условия равенства в равновесии ΔG_p=0 (для системы с постоянным давлением и температурой) и выражения для энергии Гиббса одного моля идеального газа.

Поскольку энергия Гиббса реакции равна алгебраической сумме энергий Гиббса продуктов и исходных веществ, для ΔG_pможно записать:

равна алгебраической сумме продуктов и исходных веществ реакции. является функцией температуры.

Поскольку в равновесии отношение 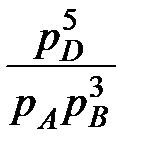= K_p, ΔG_p=0, то следует:

Из приведенных выражений следует также, что это энергия Гиббса реакции, когда все газовые компоненты взяты при давлении 1 атм. Величина для разных реакций и веществ ( образования из простых веществ) находятся экспериментально и табулируются. Их значения можно найти в справочниках термодинамических величин. Найдя из таблиц , можно рассчитать K_p, а также при любом исходном состоянии системы, т.е. p_iвсех участников реакции. Определив по ее знаку можно ответить на вопрос в какую сторону пойдет реакция при данном исходном состоянии системы.

Примеры задач для разбора на занятии:

1. В трубчатый металлургический реактор постоянного сечения равномерно по сечению подают 1000 м³/ч (в расчете на нормальные условия) газа при температуре 25 °С. Давление в реакторе постоянно и равно 1 атм. В реакторе газ постепенно нагревается до температуры 1100 °С (на выходе). Рассчитать,во сколько раз возрастет скорость газа на выходе из реактора.

Решение. Скорость газа (w) равна отношению объемного расхода газа (V) через сечение к площади сечения (S):

w=V/S

Тогда:

w₂/w₁=V₂/V₁

Из уравнения Клапейрона – Менделеева при постоянстве давления следует:

V₂/V₁ = T₂/T₁= (1000+273)/(25+273)=4,27

2. В закрытой системе газ с исходным давлением 1 атм. Нагревается с температуры 25 °С до 250 °С. Определить давление газа после нагревания.

Задачу решает студент у доски.

V= nRT/P; nR∙298/1 = nR∙523/P; P = 523/298 = 1,76атм

2^/. Т ребуется определить, какое количество кислорода запол­няет сосуд емкостью 20 л при давлении 120 ат и температуре 20° С (Т = 293° К).

По уравнению Клапейрона – Менделеева

n = PV/RT = 120*20/0,082 ∙ (273+20) = 99,9г-моль кислорода или

32 ∙ 99,9 = 3196 г, 3,2 кг

Если из этого сосуда израсходуют, например, 1,2 кг кисло­рода, то оставшийся кислород (3196 -1200 = 1996 г) будет ока­зывать давление на стенки сосуда при той же температуре по уравнению

P = GRT/MV = 1996 ∙ 0,082 ∙ 293/32 ∙ 20 = 74,93атм

2^//. Сернистый газ в количестве 100 м³ находится под давлением 820 мм рт. ст. при температуре 230° С. Определить объ­ем, занимаемый газом при нормальных условиях (0°С и 1 ат), и вычислить плотность и вес газа при заданных условиях.

PV/T = const; (820/760)*100/503 = 1*V/273; V= 820*100*273/760*503 = 58.6 м³

n= (820/760)*100/0.082*503 = 2.62 К моль; 2,62*64 = 167,4 кг;

r = 167.4/100 = 1.674 кг/м³.

3. Определить равновесное давление p_O2 в газовых смесях CO-CO₂ и H₂-H₂O при p_CO2/p_CO =0,25, T=1600 °C и p_H2O/p_H2=0,25, T=1600 °C.

Решение. Вариант 1 (для смеси CO-CO₂)

Запишем реакцию с участием указанных компонентов.

CO+1/2O₂=CO₂

; откуда

Определяя Kp из выражения Kp=exp(-ΔG⁰/RT), можно определить равновесноеp_O2 при известном отношении p_CO2/p_CO.

Значение ΔG⁰ для реакции находим их термодинамических таблиц или баз данных.

ΔG⁰ = -282695 +87,585 ^. TДж/моль (Казачков Е.А. Расчеты по теории металлургических процессов. - М.: Металлургия, 1988. - 288 с.)

Для T=1600 °C ΔG⁰ = -118648 Дж/моль.

Kp = exp(-ΔG⁰/RT) = exp(118648/8,319*1873) = exp(7,615) = 2028,4

P_O2 = (P_CO2/P_CO/Kp)² = (0,25/2028,4)² = 1,51∙10^-8атм

Подставляя данное значение ΔG⁰ в выражение для p_O2, получим:

p_O2 = 1,49 ^. 10^-8 атм.

Такие низкие значения парциального давления кислорода позволяют не учитывать его в материальном балансе смеси (тогда, когда в принципе возникает необходимость рассчитывать материальный баланс в такой смеси газов).

Аналогично находится решение для второго варианта исходных данных данной задачи- смеси H₂-H₂O. Решение проводится студентом.

Ответ. p_O2 = 5,23^.10^-10 атм. (ΔG⁰ = -246115 +54,12 ^. T)=-144748 Дж/моль

4.Как изменится P_O2 в системе при снижении температуры в таких системах.

Аналогичный расчет показывает, что для 1200 °С при том же отношении газовых компонентов парциальное давление кислорода снижается соответственно до 7,77 ^. 10^-13 и до 9,74 ^. 10^-14 атм.

5. Рассчитать равновесный состав газовой смеси H₂-S₂-H₂S при исходном количестве компонентов: H₂=0,5 моля; H₂S=0,5 молей и S₂=0 молей. Общее давление 1 атм., температура 1000 °С.

В условиях данной задачи исходно система неравновесна. Необходимо определить состав равновесной смеси, которая образуется после протекания химических взаимодействий между компонентами исходной смеси. Запишем реакцию:

H₂S=H₂ + 1/2S₂

Допустим к моменту наступления равновесия прореагировалоx молей H₂S. Тогда в равновесной смеси будет следующее количество молей компонентов:

n_H2 =0,5+x

n_S2 = x/2

n_H2S = 0,5-x

Всего молей в равновесии будет 1+x/2.Соответственно, мольные доли газовых компонентов в равновесии составят:

N_H2 = (0,5+x)/(1+x/2)

N_S2 = x/(2+x)

N_H2S = (0,5-x)/(1+ x/2)

Поскольку p_i=p_об ^. N_iдля Крможно записать:

После преобразований получим:

ΔG⁰=-91691+50,62 ^. T = -27251,7 Дж/моль.

Kp=exp(-ΔG⁰/RT)=13,15

Подставив значение Кр в выражение для Кр получим уравнение с одним неизвестным, решение (аналитическое или численное) которого даст нам значение x, которое позволит рассчитать равновесные содержания компонентов в газовой смеси.

Не нашли, что искали? Воспользуйтесь поиском: