Понятие о диаграммах состояния трехкомпонентных систем

В трехкомпонентных системах при постоянном давле­нии максимальное число сосуществующих фаз равно 4 (С = 0-3-1-Ф). Если в такой системе имеется толь­ко одна фаза (Ф=1), то число степеней свободы рав­но 3, следовательно, для построения диаграммы состоя­ния необходимы три оси координат: для температуры и концентраций каких-либо двух компонентов. Это, одна­ко, затрудняет наглядное представление концентрации третьего компонента. В. Гиббс предложил представлять концентрации всех компонентов с помощью равносто­роннего треугольника. Вершины треугольни­ка соответствуют чистым веществам А, В и С, где кон­центрации каждого из них составляют 100%. Стороны треугольника разбиты на 100 или 10 частей и представля­ют составы трех двухкомпонентных систем А—В, А—С и В—С. Любая точка внутри треугольника характеризуется тем, что сумма перпендикуляров, опущенных из нее на стороны, есть постоянная величина, равная высоте треугольника, которая принимается равной 100%. Каж­дая из равных между собой трех высот делится на 100 частей (проценты). Соответственно длины указан­ных перпендикуляров, опущенных из данной точки, на­пример D, составляют определенную долю от высоты и равны содержаниям компонентов, т. е. Dа+ Db+Dс = ВН = 100%, Dа = %A = 20%, Db = % В = 30% и Dс = % С = 50%. Из свойств равносторонних треугольников вытекает и другой способ выражения состава, в котором за 100% принимается длина стороны и наносится сетка из линий, параллельных каждой из сто­рон. В этом случае сумма трех отрезков, исходящих из точки D и оканчивающихся на сторонах треугольника, также является постоянной для любой точки и равна стороне. На рис. такие отрезки показаны пунктиром и заканчиваются стрелками. Таким образом, Dа + Db' + Dc = AB =AC =BC= 100 %, и

Важно отметить, что линии, параллельные сторонам треугольника, представ­ляют собой геометрические места расположения точек для смесей с постоянным содержанием одного компонен­та. Например, линия соответствует смесям с 70% В. Линии, соединяющие вершины с противопо­ложными сторонами треугольника, также являются гео­метрическими местами точек, а именно они передают со­став смесей с постоянным отношением концентраций двух компонентов. Так, линия Аm передает составы смесей с постоянным отношением концентраций В и С, а высота ВН - с отношением концентраций А и С, равным 1:1.

Диаграммы состояния трехкомпонентных систем нельзя изобразить на плоскости, так как еще один пара­метр - температуру (при условии постоянства давле­ния) - следует откладывать по осям, перпендикулярным плоскости концентрационного треугольника. Такая объ­емная диаграмма для простейшего случая неограничен­ной растворимости в жидком состоянии и полного отсут­ствия растворимости в твердом состоянии представлена на рис. Каждая из трех вертикальных плоскостей представляет диаграмму состояния бинарных смесей: А—В, А—С и В—С. Три криволинейные поверхности ликвидуса Ае₁Ее₂, Ве₁Ее₃ и Се₂Ее₃ представляют геомет­рические места точек, где при определенных составах и температурах кристаллизуются чистые компоненты А, В и С. Пунктирные кривые е₁Е, е₂Е и е₃Е принадлежат одновременно двум поверхностям ликвидуса, т. е. отве­чают одновременной кристаллизации двух компонентов. Так, кривая е₁Е показывает изменение состава тройно­го расплава в.зависимости от температуры при кристал­лизации А и В или, что то же самое, описывает пониже­ние температуры плавления двойной эвтектики А—В при прибавлении компонента С. Три кривые е₁Е, е₂Е и е₃Е пересекаются в точке равновесия Е между кристал­лами А, В и С и расплавом, состав которого отвечает тройной эвтектике. Система при этом не имеет степеней свободы (С=3+1-4 = 0).

Сечения объемной диаграммы горизонтальными пло­скостями представляют собой изотермические разрезы тройных систем. Например, сечение при Т₁ представляет треугольник, где криволиней­ная область хуС ограничивает двухфазное равновесие - кристаллы С и тройной расплав. Для удобства объем­ную диаграмму можно представить в виде проекции на плоскость концентрационного треугольника. Линии е'₁Е', е'₂Е' и е'₃Е' суть проекции кривых кристал­лизации двойных эвтектик е₁Е, е₂Е и е₃Е. Области А'еЕ'е'А', В'е Е'е'а В' и С'е' Е'еС' - проек­ции трех поверхностей ликвидуса. Линии, образующиеся при изотермических сечениях поверхностей ликвидуса, подобные ху на рис, также проектируют на плос­кость концентрационного треугольника. Такие изотермы для температур Т₁, Т₂, Т₃ (Т₁> Т₂> Т₃) показаны на рис..

Подобные диаграммы позволяют проследить за прекращениями, происходящими при охлаждении расплава. Если состав последнего отвечает точке Q, то при Т₂ из него начинает кристаллизоваться компонент А. Как при дальнейшем охлаждении будет изменяться со­став жидкости? Очевидно, что отношение между концен­трациями остальных двух компонентов по мере выделения А изменяться не будет. Как отмечалось выше, в этом случае составы смесей лежат на линии, соединяющей вершину треугольника с его противоположной стороной, и пашем случае - на линии А'Q. При дальнейшем ох­лаждении ниже Т₂ состав расплава будет изменяться по прямой, являющейся продолжением А'Q. Такое измене­ние будет продолжаться до того, как начнется кристал­лизация эвтектики A+B в точке D. Вследствие этого расплав будет обогащаться компонентом С, что приве­дет при дальнейшем охлаждении к изменению состава по кривой DЕ', и, наконец, к кристаллизации при более низкой температуре тройной эвтектики A+В+С.

Задача 1. Над составом (система Fe-O) 26% O₂ по массе, температура 1000°С, находящимся в состоянии равновесия о газовой фазой, снизили давление кислорода на I мм рт.ст. Определить конечный состав фаз после установления нового равновесия.

Решение (ответ).

Точка заданного состава принадлежит гетерогенной области, в которой в состоянии равновесия находятся конденсированные фазы (вюстит кислородного края области гомогенности, магнетит железного края области гомогенности) и газовая фаза. Согласно правилу фаз Гиббса С = 1. Задав температуру, использовали единственную степень свободы. Произвольное изменение давления кислорода над заданным составом приведет к нарушению равновесия: фигуративная точка переместится в область гомогенности вюстита.

Рисунок 1. Диаграмма состояния системы Fe-O

Задача2.

Пользуясь диаграммой FeOответьте на вопросы:

1. Чему равна температура плавления железа?

2. Чему равна температура плавления магнетита?

3. Чему равен нижний температурный предел существования вюстита?

4. Укажите область наиболее легкоплавких составов.

Задача3.

Пользуясь Т-Х проекцией фазовой диаграммы Сu-S, определить, могут ли жидкие высший и низший сульфиды меди одновременно сосуществовать в равновесии с газовой фазой.

Решение (ответ).

Согласно диаграмме Cu-SCuSсуществует только в твердом виде и при температуре не выше 507 °С. Т.е. это соединение даже при давлении паров серы 1 атм. еще в твердом виде разлагается на низший сульфид Cu₂Sи серу.

Ответ. Ж идкие высший и низший сульфиды меди одновременно сосуществовать в равновесии с газовой фазой не могут.

Рисунок 2. Диаграмма состояния системы Cu-S

Задача4.

Пользуясь диаграммой состояния Cu-S определите:

1. Температуру плавления чистой меди.

2. Растворимость серы в меди при температуре 1200 °С.

3. Состав сульфидного расплава, из которого при 1200 °Cвыделяется металлическая фаза. Дать примерный ее состав.

Задача 5.

Используя диаграмму FeO-Fe₂O₃-SiO₂ответьте на вопросы:

1. Назовите область наиболее легкоплавких составов.

2. Чему равна растворимость магнетита в шлаке с содержанием 30 % SiO₂ при температуре 1300 °С.

Рисунок 3. Диаграмма состояния системы FeO-Fe₂O₃-SiO₂

Решение.

1. Наиболее легкоплавкие составы соответствую области фаялитовых шлаков (показать область). Температура ликвидус таких шлаков менее 1200 С.

2. Провести прямую, соответствующую составам шлаков с содержанием кремнезема 30 % до пересечения с изотермой 1300 °С. Определить состав шлака в точке пересечения (концентрацию в нем FeO, Fe₂O₃иSiO₂). Пересчитать состав шлака исходя из условия, что в шлаковом расплаве железо присутствует в FeOи Fe₃O₄.

Задача 6.

Объяснить, как и почему изменится вязкость шлакового расплава, отвечающего составу 20% SiO₂ и 80% FеО (далее точка А), если равновесное давление кислорода в этой системе повысить до 10^-4ат.

Решение (ответ).

Вязкость шлакового расплава возрастет, т.к. при повышении давления кислорода, до 10^-4ат в расплаве появятся (увеличится содержание) катионы Fе⁺³ и шлак станет гетерогенным (выделится магнетит). Используя диаграмму состояния FeO-Fe₂O₃-SiO₂, можно определить, какое количество кристаллов магнетита выпадет из расплава при заданных условиях. Для этого из точки А нужно провести линию, параллельную основанию, до пересечения с изобарой 10^-4ат в точке 0 (состав шлака остается постоянным по SiO₂). Точка 0 описывает новое состояние равновесия двух конденсированных фаз (твердой, представленной магнетитом, и жидкой) с газовой фазой. Для определения количества твердой и жидкой фаз нужно точку С соединить с точкой К, отвечающей составу магнетита, и продолжить линию до пересечения с пограничной кривой в т.С. Состав жидкой фазы определяется т.С, количество жидкой и твердой фаз - по правилу рычага отрезками ОК/КС и ОС/КС соответственно.

Задача 7.

Используя диаграмму Cu-Fe-Sответьте на вопросы:

1. Какие штейны, бедные или богатые более богатые склонны к металлизации (т.е., в каких штейнах возможны большие отклонения от стехиометрических сульфидных расплавов без выделения металлической фазы)?

2. Возможно ли выделение из бедных штейнов металлического расплава на основе меди?

3. Возможно ли выделение избогатых штейнов металлического расплава на основе меди?

4. Металлическая фаза на основе какого металла (Cuили Fe) будет выделяться из бедных штейнов при снижении содержания в них серы?)

Рисунок 4. Изотермический разрез системы Сu-Fe-S при 1523 К

Ответы.

1. В большей степени (более склонны) могут быть металлизированы без выделения металлической фазы бедные штейны. Более богатые штейны практически не металлизируются, поскольку даже при небольшом уменьшении содержания по сравнению со стехиометрией из сульфидного расплава будет выделяться медная фаза.

2. Нет.

3. Да.

4. Из бедных штейнов при их десульфуризации будет выделяться фаза твердого раствора на основе γ-Fe

Тема 5. Расчеты термодинамики процессов диссоциации (2 часа)

В пирометаллургических процессах при высоких температурах устойчивые при обычных условиях оксиды и сульфиды металлов способны диссоциировать на составляющие элементы. Полнота протекания этого процесса определяется температурой и давлением, а также зависит от характера и силы химической связи.

В общем виде для двухвалентного металла реакцию диссоциации можно записать:

(1)

Рисунок 5.1Зависимость упругости диссоциации некоторых оксидов

Равновесное давление кислорода (серы), развивающееся при диссоциации оксида (сульфида) металлического края области гомогенности при данной температуре называется упругостью диссоциации оксида (сульфида.). Зависимость упругости диссоциации оксидов от температуры представлена нарисунке 5.1. Направление протекания обратимой реакции (1) определяется соотношением величин упругости диссоциации оксида (сульфида) и парциального давления кислорода (серы) в зоне реакции . При протекает реакция диссоциации до тех пор, пока парциальное давление кислорода в газовой фазе не станет равным равновесному давлению или пока весь оксид не продиссоциирует. В случае, когда идет окисление металла до тех пор, пока парциальное давление не станет равным или пока весь металл не окислится. И в случае, когда , имеет место динамическое равновесие. По величине упругости диссоциации можно судить о прочности соединений Me-O и о сродстве металлов к кислороду (сере). Чем выше давление диссоциации, тем меньше прочность химических связей. На рисунках 5.2 и 5.3 представлены температурные зависимости упругости диссоциации ряда оксидов и сульфидов. Эти зависимости позволяют оценить возможность нахождения металлов при определенной температуре и заданном парциальном давлении кислорода (серы) в свободном состоянии или в виде соединений.

Рисунок 5.2Температурная зависимость упругости диссоциации оксидов

, где (2)

- величина, характеризующая исходное состояние системы (неравновесное);

- константа равновесия реакции.

Величина определяет направление реакции. При стандартных условиях это выражение принимает следующий вид:

Рисунок 5.3Температурная зависимость упругости диссоциации сульфидов

Для сравнения сродства металлов к кислороду (сере, хлору) стандартный термодинамический потенциал образования оксидов (сульфидов, хлоридов) из элементов всегда относят к одному молю кислорода (серы, хлора). Чем меньше значение стандартного термодинамического потенциала образования оксида, сульфида, тем прочнее связь MeO (MeS).На различии в сродстве металлов к кислороду и сере основаны процессы окислительного рафинирования металлов и рафинирование с помощью серы.

Рассмотрим некоторые типовые примеры задач.

Пример 1.

Медный сульфидный концентрат нагревается в печи. В состав концентрата помимо сульфидов входят карбонаты кальция и магния. Рассчитать при какой температуре начнут разлагаться (диссоциировать) CaCO₃ и MgCO₃, если в газовой фазе печи содержится 30 % CO₂. Общее давление в печи 1 атм. Какой из карбонатов менее прочный, а какой- более?

Решение.

Запишем уравнение реакции диссоциации известняка

CaCO₃ = CaO +CO₂ (4)

Если нагрев достаточно медленный, чтобы считать, что в каждый момент времени система близка к равновесию, то в момент начала диссоциации известняка в системе будут присутствовать две фазы чистого известняка(CaCO₃)и известь (CaO). Тогда:

Kp₄ = p_CO2 = exp(-ΔG⁰/RT)

При этом, процесс диссоциации начнется в момент, когда равновесное давление газового компонента (CO₂) будет равно (или более) его давления в газовой фазе, т.е. процесс диссоциации начнется при:

Kp₄ = p_CO2 = exp(-ΔG⁰/RT)=0,3

Тогда:

-ΔG⁰/RT =ln(0,3) = -1,204

ΔG⁰/RT= 1,204

ΔG⁰ = 170577 – 144,19 ^. T

Тогда:

20526,7/T – 17,35 = 1,204

Откуда:

T=1106 K=833 °C

Аналогично проводится расчет для MgCO₃ (студенты проводят у доски)

-ΔG⁰/RT = ln(0,3) = -1.204

ΔG⁰/RT= 1,204

ΔG⁰ = 110825 - 120,16 ^. T

Тогда:

13336,3/T – 14,46 = 1,204

Откуда:

T= 851K=578 °C

Расчеты показывают, что менее прочным является карбонат магния, поскольку его диссоциация при прочих равных условиях начинается при более низкой температуре.

Пример 2.

Рассчитать, как изменится температура диссоциации карбоната кальция при увеличении содержания CO₂ в газовой фазе до 100 %.

Студенты проводят расчет сами у доски.

Ответ:t=910 °C. (для MgCO₃–649 °С)

Пример3.

Вакуумирование системы будет способствовать или препятствовать процессу диссоциации оксидов (т.е., при вакуумировании соединения легче диссоциируют или труднее). Вывод подтвердить теоретическими положениями и расчетами.

Решение.

Прежде всего, необходимо определиться, что значит соединение легче диссоциирует, или труднее. Как видно из диаграмм, любое соединение при нагревании до определенной температуры начинает разлагаться. Естественно, что:

Cсоединение, которое разлагается при меньшем нагреве (меньшей температуре) является менее прочным и легче диссоциирует. Менее прочным и легче диссоциирующим является также соединение, которое при одной и той же температуре имеет более высокую упругость диссоциации, т.е. оно начинает разлагаться при более высоком давлении кислорода (серы, хлора и т.д.) во внешней газовой среде.

Ответить на вопрос можно с использованием диаграмм, а также проведя простейшие расчетные оценки для конкретного оксида.

Решение проводят студенты у доски.

Ответ. В соответствии с диаграммами, например, на рисунках 5.1-5.3, при снижении внешнего давления температура начала разложения снижается, т.е. диссоциация протекает легче.

Пример 4.

Определить какой из сульфидов является более устойчивым CuSилиFeS. При какой температуре диссоциирует первый, а при какой (по мере повышения температуры) второй сульфид.

Решение.

Сравнительную устойчивость соединений можно оценить по величине упругости диссоциации или по температуре, при которой происходит разложение соединения. Выбираем первый способ сравнения устойчивости.

Итак, необходимо рассчитать упругость диссоциации сульфидов, но она зависит от температуры, которая не задана. Допустим оба сульфида нагревают до температуры, например, 600 °С. Запишем реакции диссоциации сульфидов (высшие сульфиды вначале диссоциируютна низшие):

2CuS = Cu₂S + ½ S₂ (5)

FeS = Fe + ½ S₂ (6)

Kp₅ = p_S2^0,5= exp(-ΔG₅⁰/RT)

Kp₆ = p_S2^0,5= exp(-ΔG₆⁰/RT)

Из таблиц термодинамических данных:

ΔG₅⁰ = -4474,78Дж/моль; ΔG₆⁰ = 104448 Дж/моль.

Равновесноеp_S2первой реакции составило 3,43 атм.,
а для второй 3 ^. 10^-13 атм.

Видно, что упругость диссоциации для сульфида меди во много раз превышает ее для сульфида железа, что свидетельствует о более высокой прочности последнего.

Пример 5.

Рассчитать при какой температуре будет разлагаться пирит (FeS₂)при давлении паров серы 1 атм.

Решение.

Прочность соединения определяется не только видом соединения, но и внешними условиями, в частности величиной внешнего давления паров неметалла, входящего в состав соединения.

Порядок решения аналогичен решению предыдущей задачи с той только разницей, что задается не температура, а величина равновесного давления S₂, а температура рассчитывается. Решение проводят студенты у доски.Как изменится температура диссоциации пирита при снижении внешнего давления паров серы до 0,1 атм.?

Пример 6. Ампулу, в которую помещена смесь оксидов меди и железа, откачали до глубокого вакуума, нагрели до 800°С и выдержали до установления равновесия. Какие реакции будут протекать в ампуле? Какие конечные продукты можно получить?

Решением (ответ). По температурной зависимости упругости диссоциации оксидов определяем = I0^-10ат и =I0^-20ат при 800°С. В ампуле будет протекать реакция диссоциации: 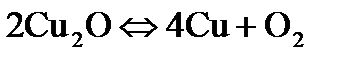до установления равновесного давления = I0^-10. По отношению к вюститу в ампуле создается окислительная атмосфера, т.к. , следовательно, вюстит будет окисляться по реакции: .

Упругость диссоциации при 800°С - = I0^-18. В данных условиях магнетит стехиометрического состава будет окисляться по реакции , и его состав перейдет внутрь области гомогенности магнетита. Так, при достаточно большом количестве в ампуле конечными продуктами после установления равновесия будут: , Cu, 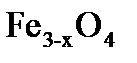и газовая фаза, содержащая кислород - = I0^-10ат.

Тема 6. Расчеты процессов окисления металлов и сульфидов(2 часа)

Окислительные процессы играют важную роль в металлургии цветных металлов. Металлургам весьма часто приходится сталкиваться как с окислением металлов (жидких и твердых), так и с окислением сульфидов. Рассмотрим некоторые примеры процессов окисления.

Задача 1. Для получения оксидной пленки Cu₂O на поверхности медной проволоки длиной (L)200 мм и диаметром (d)1 мм ее поместили в закрытую систему при Т=____ первоначально заполненную чистым СО₂(давление 1 атм.) Рассчитать, каким должен быть объем ампулы, чтобы образовавшийся слой оксида имел толщину(Δ) 1 мкм.

1. 1000 К, 2.1010 К, 3. 1020 К, 4. 1030К

Решение.

Запишем реакцию окисления меди CO₂.

2Cu+CO₂=Cu₂O+CO

Допустим, плотность Cu₂O при заданных температурах составляет 7,5 г/см³ (студентам – уточнить плотность Cu₂O). Рассчитаем массу оксидной пленки. Объем пленки составит:

V_Cu2O= Lπ ((d+2Δ)²-d²)/4 = 0,6286мм³

Масса оксида составит:

M_Cu2O= V_Cu2O*ρ_Cu2O=4,71*10^-3

По стехиометрии на образование такого количества оксида должно израсходоваться CO₂:

V_CO2 = M_Cu2O/µ_Cu2O*22,4=7,38*10^-4л

Однако, полностью CO₂не должен израсходоваться, к моменту образования пленки система должна находиться в равновесии.Считая, что активность меди и оксида равны единице, получим

CO/CO₂=Kp=exp(-ΔG⁰/RT)

ΔG⁰ (из ТБ)=121516-21 ^. Т Дж/моль, тогда:

ΔG⁰_1000K=100516 Дж

Kp=5,58*10^-6, т.е. в равновесии объем CO₂ должен составить (по стехиометрии объем образующегося CO будет равен объему прореагировавшего CO₂, т.е. 7,38*10^-4л):

V_CO2^равн=7,38*10^-4/(5,58*10^-6)=132,208 л, а с учетом прореагировавшего CO₂ в исходной ампуле его должно быть:

V_CO2^исх= V_CO2^равн+ V_CO2^расх=132,209 л.(при н.у.)

Для того, чтобы при температуре 1000 К в ампуле был необходимый объем CO2 ее (ампулы) объем должен составить:

V_амп.=132,209*1000/273=484,3 л

Иначе говоря, для создания пленки толщиной всего 1 мкм на проволоке длиной 200 мм при 1000 К потребуется ампула объемом почти 0,5 м³.Заранее казалось, что этот объем будет существенно меньше. Данный пример показывает, насколько важно проводить конкретные расчеты, не полагаясь на общие представления и грубые оценки.

Проверить на следующем занятии.

Задача 2. Какие будут протекать реакции при окислении Cu₂S при Т=500°С и = 10^-10ат в случае постепенного увеличения в газовой фазе?

Решение (ответ). Для рассмотрения возможных процессов окисления Cu₂O воспользуемся потенциальной диаграммой Cu–S–O при Т=500°С. Реакции будут протекать в следующей последовательности:

Задача 3.

Рассчитать остаточную концентрацию Ni в черновой меди, если ее окисление ведется до начала образования Cu₂О при Т=___ ^оС.

1. 1100^оС; 2. 1120^оС; 3. 1130^оС

Решение проводим с использованием Термобэйс. Коэффициент активности никеля в меди принимаем равным 1.

Задача 4.

Рассчитать, какие фазы образуются в результате окисления FeS, если при Т=___К давление О₂ составляет ___, а давление S₂ ____соответственно:

1. 1000 К, 10^-5, 10^-20;

2. 1100 К, 10^-10, 10^-15;

3. 1200 К, 10^-15, 10^-10;

4. 1300 К, 10^-20, 10^-5;

Задача5.

Рассчитать и построить потенциальную диаграмму в системе Zn-S в диапазоне температур 500-1000 K.

Задача6.

Рассчитать и построить потенциальную диаграмму в системе Zn-S-O в диапазоне температур 500-1000 K.

Задача7.

Рассчитать при какой температуре будет разлагаться сульфат кальция в атмосфере, содержащей 40 %, 1 % O₂, остальное азот и SO₃. Общее давление равно 1 атм.

Тема 7. Расчеты термодинамики процессов восстановления чистых оксидов и в растворах(2 часа)

Процессы восстановления оксидов имеют большое практическое значение при получении чернового металла из руд и при рафинировании его от примесей. Помимо оксидов, объектами восстановления могут служить галогениды и сульфиды. В качестве восстановителей применяют: оксид углерода, метан, твердый углерод, водород, различные металлы, обладающие большим сродством к аниону.

В общем виде реакция восстановления оксидов с помощью СО или водорода может быть записана следующим образом:

(1)

Восстановление MeO будет протекать, если , при 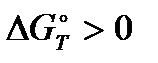будет протекать окисление Me, при система будет в состоянии равновесия. Реакция (1) протекает без изменения числа газообразных молекул, поэтому общее давление не влияет на равновесие реакции и данную систему условно можно считать моновариантной. Задав температуру, мы получим строгое соотношение между равновесными давлениями и и, наоборот, любому заданному давлению восстановителя в равновесных условиях отвечает строго постоянная температура.

При восстановлении некоторых металлов равновесное содержание CO в газовой фазе не превышает нескольких процентов, тогда как других восстанавливаются газовой фазой, состоящей почти из одногооксида углерода. В реальных пирометаллургических процессах гораздо чаще восстановлению подвергаются оксиды, находящиеся в растворе в других оксидах (силикатах, алюминатах и др.). Нередко и образующийся металл также присутствует в растворе в другом металле или сульфиде. В этом случае константа реакции восстановления (1) запишется следующим образом:

, где

а_Me – активность металла в сплаве,

а_MeO – активность оксида в шлаковом расплаве.

Откуда равновесное отношение в газовой фазе

будет возрастать с увеличением активности оксида в расплаве и с уменьшением активности металла. При восстановлении оксидов из шлакового расплава по мере уменьшения их концентрации (активности) потребуется более восстановительная газовая фаза. Снижение активности (концентрации) металла в растворе наоборот требует менее восстановительной атмосферы. По этой причине нельзя получить чистый металл при восстановлении смеси оксидов.

Рассмотрим некоторые типичные примеры задач восстановления оксидов газовыми смесями.

Задача 1. Рассчитать концентрацию H₂ в газовой смеси H₂-H₂О, которая позволяет восстановить Ni из его оксида при температуре ___К.

1. 1000 К; 2. 1100 К; 3. 1200 К; 4. 1300 К.

Решение:

Запишем реакцию: NiO + H₂ = Ni + H₂O

Константа равновесия этой реакции запишется (учитывая, что NiOи Ni присутствуют в рассматриваемой системе в чистом виде, т.е. в стандартном состоянии, а активность газовых компонентов равна парциальному давлению, если в качестве стандартного состояния для газов выбирается p_i=1 атм.):

Если принять, что газовая фаза состоит из водорода и воды и общее давление в системе 1 атм., то можно записать второе уравнение P_H2O + P_H2 = 1

Стандартную энергию Гиббса реакции находим из таблиц термодинамических данных.

Далее, решая систему уравнений, находим P_H2, => и %H₂,

Рассчитав (расчеты проводят студенты у доски) равновесное содержание водорода в рассматриваемой системе строим график зависимости равновесного %H₂от температуры. Вместе со студентами анализируем (с точки зрения термодинамики) рациональность повышения температуры для процесса восстановления закиси никеля газовой смесью H₂-H₂О.

При расчете и анализе термодинамики процессов восстановления газовыми смесями может ставиться и обратная задача – поиска необходимой для протекания провеса восстановления температуры при известном составе газовой смеси. Например,

Задача 2. Рассчитать при какой температуре возможно получение вольфрама из его оксида WО₂, если газовая фаза содержит __ % СО.

1. 10%; 2. 20%; 3. 30%; 4. 40%

Решение:

Запишем реакцию:

1/2WO₂ + CO = 1/2W + CO₂

Константа равновесия этой реакции запишется как:

Если принять, что газовая фаза состоит из CO и CO₂ и общее давление в системе 1 атм., то P_CO2 + P_CO = 1 и зная %СO можно найти P_СO и P_CO2, а => и их отношение.

Тогда, зная ΔG⁰T = a + bT, получим уравнение:

ln(P_CO2/P_CO)=(-a-bT)/(RT)

Решим его и найдем T.

В расчетах восстановления оксидов газовыми смесями из расплавов или в расплавы (т.е. когда исходные вещества или продукты находятся не в чистом виде, а в растворах) потребуется знание активности (или коэффициентов активности) компонентов в растворах. Активность компонентов растворах можно найти в справочниках и специализированной литературе, либо (в отсутствие экспериментальных данных) рассчитать с использованием той или иной модели растворов. В последнем варианте расчеты могут дать более грубые оценки.

Задача 3. Рассчитать процент СОв газовой фазе, которой возможно провести восстановление Fe (считаем, что железо получается в чистом виде) из FeO-SiO₂ шлака. Условия процесса следующие: T=___, содержание FeO в шлаке составляет 80 %(вес).

1. 1900 K; 1950 K; 2000 K; 2050 K;

Задача решается аналогично первой, за исключением того, что активность FeO в шлаке не равна 1. Для того чтобы ее определить используем модель Темкина. Для этого надо сначала пересчитать весовые проценты в молярные. Если шлак состоит из только из FeO и SiO₂ то это легко сделать.

Затем можно рассмотреть следующие реакции:

1) FeO = Fe²⁺ + O^2-

2) SiO₂ + 2O^2- = SiO₄^4-

Возьмем 100 моль шлака, тогда:

аналогично

Тогда можно посчитать катионные и анионные доли:

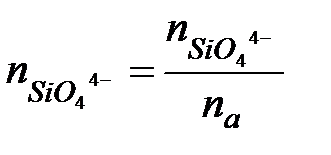
по всем реакциям

Для того чтобы посчитать активность компонента FeO нужно записать константы равновесия для реакции 1 и приравнять ее 1, тогда учитывая, что активности ионов равны их ионной доле, можно найти активности компонентов.

Задача 4. Рассчитать поток кислорода и требуемое обогащение дутья по кислороду (дутье состоит из кислорода и азота) в топку для сжигания пылеугля, если поток угля составляет 2 кг/мин, температура, развиваемая в топке составляет 2000 К, а требуемое содержание СО в выходящем из топки газе должно быть равно: __% (считаем, что уголь сгорает полностью, содержание углерода в угле условно считаем равным 100 %)).

1. 70%; 2. 75%; 3. 80%; 4. 85%.

Решение:

1. Газовая смесь состоит только из СO и CO₂ => зная количество C(моль) и процент CO можно посчитать по балансу количество CO и CO₂ (моль), а следовательно и количество O₂.

2. Однако если подавать чистый кислород, то температура будет выше 2000. Необходимо посчитать еще количество N₂.

Для этого необходимы дополнительные данные.

по теплоемкости газов:

С_p^CO2=44,14 + 9,04 ^. 10^-3T – 8,54^.10⁵/T²

С_p^CO=28,41 + 4,1 ^. 10^-3T –0,46^.10⁵/T²

С_p^N2=27,87 + 4,27 ^. 10^-3T

тепловые эффекты реакций:

1. C + 0,65O₂ = 0,7 CO + 0,3CO₂ ΔH=-202080 Дж/моль

2. C + 0,625O₂ = 0,75 CO + 0,25CO₂ ΔH=-188464 Дж/моль

3. C + 0,6O₂ = 0,8 CO + 0,2CO₂ ΔH=-174261 Дж/моль

Для других вариантов исходных данных другие стехиометрические коэффициенты в последних уравнениях и другие тепловые эффекты реакций. Эти варианты просчитываются студентами у доски.

Пользуясь стехиометрическими коэффициентами последних уравнений, находим решение первой части задачи, т.е. количество кислорода (V_O2), необходимое на сжигание угля. Далее находим общее количество тепла, выделяемое по этим реакциям:

Q_Σ=Q₁ +Q₂ + Q₃ = (V_O2(1) ^. ΔH₁/0,65+ V_O2(2) ^. ΔH₂/0,625+ V_O2(3) ^. ΔH₃/0,6)/22.4

Решение второй части задачи.

Тепло на нагрев 1 моля газа i от 298 Kдо температуры T рассчитывается по формуле:

Интегрируя данное равнение (с использованием приведенных выше уравнений для расчета теплоемкостей) рассчитывается тепло на нагрев COиCO₂. Тепло на нагрев азота рассчитывается по разности между суммарным теплом от сжигания угля и затрачиваемым теплом на нагрев COиCO₂. Далее, пользуясь последним уравнением, находим V_N2в дутье и состав дутья (посчитан ранее V_O2).

Задача 5. В закрытую ампулу объемом 2 литра поместили ___ граммов PbO и заполнили ее газовой смесью, состоящей из __%H₂ и ___% H₂O под давлением 2 атм. при Т= ____. Рассчитать массу свинца, перешедшего в газовую фазу.

<PbO> + (H₂) = (Pb) + (H₂O) ΔG⁰= 116297 - 102*T

1. 40 гр, 20%, 80%, 900 K

2. 50 гр, 15%, 85%, 920 K

3. 60 гр, 10%, 90%, 960 K

4. 70 гр, 18%, 82%, 1000 K

Решение:

Задача решается как классическая задача поиска равновесия в закрытой системе. Предварительно необходимо рассчитать кол-во моль PbO, H₂, H₂O

1. Обозначим переменные <PbO>-x₁; (H₂)-x₂; (Pb)-x₃; (H₂O)-x₄

2. Необходимо 4 уравнения:

a. 3 уравнения баланса по элементам

в. 1 уравнение закона действующих масс.

3. Найдя x₃(моль) можно рассчитать массу (Pb).

Численное решение данной задачи студенты проводят самостоятельно дома.

Примечание. Обсудить, что будет, если Pbобразуется больше чем его было изначально в виде PbO?

Тема 8. Восстановление оксидов твердым углеродом(2 часа)

При восстановлении оксидов в присутствии твердого углерода большое значение приобретает реакция Будуара:

(1)

Реакция (1) эндотермическая, при повышении температуры равновесие сдвигается в сторону образования CO.

Реакция Будуара протекает с увеличением объема. Согласно правилу Ле-Шателье, понижение общего давления сдвигает равновесие реакции (1) в сторону образования CO.

Процесс восстановления оксидов в присутствии твердого углерода можно рассматривать как двухстадийный:

(2)

(3)

(4)

В этом случае мы имеем дело с совмещенным равновесием двух реакций: процесса газового восстановления оксида и реакцией Будуара. Совместное протекание этих двух реакций возможно лишь выше температуры,характерной для каждого оксида.

Реакция восстановления оксидов твердым углеродом (4) может достичь равновесия только в том случае, если реакции (2) и (3) достигли равновесия. Общее совмещенное равновесие системы Fe–C–CO–CO₂ графически и определяется точкой 0 (рисунок 8.1).

Т.о., процессы восстановления в присутствии твердого углерода имеют определенную специфику, как с термодинамической, так и с кинетической точки зрения. Особенности термодинамики продиктованы наличием дополнительной фазы - твердого углерода в различных модификациях: уголь, кокс, графит, торф, древесина и т.д. Специфика кинетики проявляется в более сложном по сравнению с газовым восстановлением механизмом реакции.

Рисунок 8.1Совмещение кривых равновесия реакции восстановления оксидов металлов оксидом углерода и реакции С + СО2 = 2СО

Пример 1.

Реактор, наполненный древесный углем (считаем, чистым графитом) используется для синтеза смеси газов CO/CO₂, необходимой для исследования термодинамики металлургических систем. Для этого через реактор очень медленно пропускают CO₂. Скорость газа такова, что в реакторе достигается состояние термодинамического равновесия газовой фазы с твердым углеродом. Для синтеза газа с требуемым отношением CO/CO₂ необходимо знать влияние температуры на CO/CO₂. Общее давление 1 атм.

Вопрос. 1. Рассчитать зависимость равновесногоCO/CO₂ от температуры в системе с твердым углеродом. 2. Как при этом меняется равновесное парциальное давление кислорода.

Решение.

Прежде всего, используя правило фаз Гиббса убедимся, что задание температуры действительно однозначно определяет отношение CO/CO₂ в рассматриваемой системе.

Согласно правилу фаз Ф=К+2-С. В системе 2 компонента (Cи O), 2 фазы (газ и твердый углерод), одна степень свободы использована заданием общего давления, остается одна степень свободы. Таким образом, задавая температуру, мы ее используем, и после этого все параметры системы будут однозначно определены, в том числе и состав газовой фазы, т.е. содержание в ней CO, CO₂иO₂.

Для ответа на поставленный вопрос можно не привлекать правило фаз. Запишем уравнение возможной реакции между углеродом и CO иCO₂ газовой фазы:

C + CO₂ = 2CO (5)

Кр = p_CO²/(a_C ^. p_CO2)

Поскольку активность углерода равна 1 (углерод в системе присутствует в чистом виде), а содержание кислорода в таких системах пренебрежимо мало по сравнению с COи CO₂, можно принять, что:

p_CO+p_CO2 = 1, тогдаp_CO = 1-p_CO2иКр = (1-p_CO2)²/p_CO2

Поскольку Kp зависит только от температуры, получаем, что задание температур однозначно определяет p_CO2иp_CO, т.е. состав газовой фазы.

Из термодинамических баз данных находим вид зависимости ΔG⁰реакции от температуры – f(T). Тогда:

(1-p_CO2)²/p_CO2 = exp(-f(T)/RT)

Решая полученное уравнение численно или аналитически, получаем зависимость p_CO2 от температуры и p_CO/p_CO2=CO/CO₂.

Студентам предлагается дома вывести решение (численное, конечно), а также предложить решение второй части данной задачи (как влияет температура на изменение парциального давления кислорода в системе).

Рассмотренная реакция достаточно известна и носит название реакции Будуара. Вид зависимости содержания CO в газовой смеси, равновесной с твердым углеродом приведен на рисунке 8.1.

Пример 2.

Можно ли твердым углеродом при температуре 650°С (давление 1 атм.) восстановить FeO до металлического железа и почему?

Решение.

Ответ на поставленный вопрос можно получить двумя способами.

1. Можно воспользоваться приведенной выше диаграммой. Из диаграммы видно, что при температуре 650 °С над твердым углеродом в равновесной газовой смеси будет около 40 % CO. В то же время область устойчивости железа при данной температуре лежит в области составов газов, содержащих более примерно 55 %, т.е. состав газа над твердым углеродом недостаточно восстановителен, чтобы FeO восстанавливался до металлического железа.

2. Если под рукой нет диаграммы, необходимо провести термодинамические расчеты. Как показано в первой задаче задание температуры в системе с твердым углеродом однозначно определяет равновесный состав газовой фазы (т.е. % CO, CO₂иO₂) в такой системе, определяемый термодинамикой реакции Будуара (5):

Кр = p_CO²/(a_C ^. p_CO2)= (1-p_CO2)²/p_CO2

Т.о., для заданной температуры (650 °С) пользуясь термодинамическими данными мы можем рассчитать Кр реакции Будуара (Kp=exp(-ΔG⁰/RT)) и далее равновесное содержание CO и CO₂в газовой фазе (в рассматриваемой задаче мы считаем, что в системе у нас всегда избыток твердого углерода).

Из термодинамических данных:

ΔG⁰= 172130-177,76 ^. T = 8057,52 Дж/моль, тогда:

Кр=exp(-ΔG⁰/RT)=0,35

Решая квадратичное уравнение относительно P_CO2, получим:

P_CO2=0,56атм. и P_CO=1-P_CO2= 0,44 атм.Или

CO/CO₂ = 0,79

Далее задача решается аналогично рассмотренным выше примерам задач восстановления оксидов газовыми смесями известного состава. Т.е.,в начале находим равновесный состав газовой смеси в системе металл-оксид и сравниваем его с составом заданной газовой смеси (с помощью которой мы хотим восстановить оксид). В нашем последнем случае, это будет газовая фаза над твердым углеродом. Согласно реакциивосстановления FeO до Fe:

FeO+CO=Fe+CO₂ (6)

ΔG⁰= 2047,9 Дж/моль, тогда:

Кр=exp(-ΔG⁰/RT)=0,766 и

Равновесное отношение CO/CO₂ будет равно:

CO/CO₂ = 1/Kp₆ = 1,31

Равновесное содержание CO в газовой фазе составит 56,7 %.

Процесс восстановления закиси железа до Fe, т.о. будет протекать при содержании CO в газовой смеси более 56,7 %. В то же время, согласно расчетам для реакции Будуара равновесное содержание CO в газовой фазе над твердым к углеродом при температуре 650 °С составляет 44 %. Это значит, что в рассматриваемых условиях восстановления оксида железа (2) происходить не будет – устойчивым в систем с твердым углеродом при данной температуре будет FeO, а не Fe, что согласуется и с выводом, полученным первым способом.

Пример 3.

Можно ли твердым углеродом при температуре 800 С (давление 1 атм.) восстановить FeO до металлического железа и почему?

Пример полностью аналогичен предыдущему. Решение рассматривается студентами у доски.

(ответ – да, в данных условиях восстановление FeO до FeТермодинамически вероятно, т.е. будет происходить).

Пример 4.

Можно ли твердым углеродом при температуре 400 С (давление 1 атм.) восстановить Fe₃O₄ до FeO и почему?

Пример принципиально аналогичен предыдущим и отличается только набором равновесных фаз и реакциями, описывающими равновесие. Решение рассматривается студентами у доски.

(Ответ – нет, в данных условиях восстановление Fe₃O₄ до FeOтермодинамически невозможно, т.е. не будет происходить. В присутствии твердого углерода при 400 °С устойчива будет фаза магнетита. Более того, вюстит при этих температурах вообще не может существовать – см. диаграмму состояния Fe-O).

Пример 5.

Легче или труднее протекает процесс восстановления цветных металлов из шлакового расплава или свободного оксида? Объясните, почему?

Принципиально этот вопрос рассматривался на лекции и студенты должны уметь на него обоснованно отвечать. Ответ на данную задачу студенты показывает у доски

Решение.

Прежде всего, обозначим, что значит труднее или легче восстановить оксид. Будем считать, что труднее восстановить тот оксид, для восстановления которого необходима более восстановительная атмосфера, т.е. более высокие значения отношений CO/CO₂илиH₂/H₂O в газовой смеси.

Запишем реакцию восстановления какого-либо металла.

MeO + CO = Me+CO₂ (8)

1. Если металл в чистом виде получается из чистого оксида, тоa_Me=1 иa_MeO=1. Тогда, равновесное отношение COк CO₂будет равно:

CO/CO₂= 1/K_p (9)

2. Если металл получаем в чистом виде из шлакового расплава, то a_Me=1, а a_MeO<1. Равновесное отношение COк CO₂в этом случае будет равно:

CO/CO₂= 1/(K_p^.a_MeO) (10)

Очевидно, что значение CO/CO₂ в 10-м выражение будет больше, чем в 9-м, поскольку знаменатель в 10-м выражении меньше.

Это значит, что восстановить оксид из шлакового расплава труднее, чем из чистого оксида.

Пример 6.

Есть смесь материалов, состоящая из оксидов различных металлов – Fe₃O₄, Cu₂O, NiO,ZnO, Al₂O₃.Определить какие из оксидов металлов могут быть восстановлены (с получением чистого металла) углеродом при температуре 850° С.

Как это было уже показана выше, ответ может быть получен двумя способами – с использованием диаграммы на рисунке 8.1. и проведением термодинамических расчетов с определением равновесного отношения CO/CO₂ в системе MeO-Me и над твердым углеродом. Решение проводят студенты у доски.

Тема 9. Кинетика гомогенных и гетерогенных процессов. Анализ кинетических кривых. Определение лимитирующих стадий(2 часа)

Задача 1. Кинетическая кривая зависимости скорости процесса диссоциации от времени описывается уравнением:

1. v = 3,2 (1-e^-0,03t) моль/с

2. v = 0,2 (1,03 - 2/(t+3)) моль/с

3. v = 5,6 (2-1,7 e^-0,025t) моль/с

4. v = 0,02 (0,5-0,4/(t+4)) моль/с.

Вывести зависимость степени протекания процесса от времени, если известно, что в начальный момент в системе находилось 1 моль вещества. Определить момент времени, когда прореагирует все вещество.

Решение.

v=dn/dt → = 3,2(t+e^-0,03t/0,03)-3,2/0,03

Когда все вещество (1 моль) прореагирует n(t)=1, т.е.

3,2(t+e^-0,03t/0,03)-3,2/0,03=1, решить уравнение можно численными методами или графически (например, с использованием пакета Excel). На рисунке 1 приведен график интегральной функции от времени:

Полностью 1 моль вещества продиссоциирует через примерно 4,64 с (если уравнение скорости справедливо во всем диапазоне.

Аналогично решаются остальные задачи. Решение задач проводится студентами.

Задача 2. Рассчитать, сколько грамм Co образуется к 3-ей секунде, если зависимость скорости диссоциации CoO от времени следующая:

1. v = 0,2 (1,03 - 2/(t+3)) моль/с

2. v = 3,2 (1-e^-0,03t) моль/с

3. v = 0,02 (0,5-0,4/(t+4)) моль/с.

4. v = 5,6 (2-1,7 e^-0,025t) моль/с

Порядок решения аналогичен рассмотренному выше решению, только задается не количество прореагировавшего вещества, а время, и по графику (или аналитически, если удается решить) находится степень превращения или количество прореагировавшего вещества.

Задача 3. В металлургическую лабораторию поступил на исследование сплав нового материала, который предполагается использовать в окислительных условиях при высоких температурах. Средняя молекулярная масса металлов в сплаве - 56, оксида - 72. Плотность металла – 7,67 плотность его оксида – 5,2 гр/см³. Для определения параметров его окисления были проведены опыты с плоскими образцами площадью 1 см² по методу дифференциальной гравиметрии на установке SETARAM. Определить кинетические параметры процесса окисления и построить кинетическую модель процесса.

Решение

a) Построить интегральную кривую m(гр) от t(час) и сгладить ее.

b) Построить дифференциальную кривую dm/dt (гр/час)

c) Если реакция идет до конца, то в равновесии будет один оксид. Тогда его масса будет m_MeO = m_Me*M_MeO/M_Me. Отсюда можно найти степень протекания.

Построить ее график и для двух опытов с одинаковой концентрацией кислорода найти моменты времени t₁ и t₂ с одинаковой степенью протекания.

d) Скорость внутренней диффузии определяется

V=dm/dt = D*(C_пов. – C_гр.)*S/d

где: C_пов. - концентрация реагента на поверхности;

C_гр. - концентрация реагента на границе раздела фаз (~0)

S - площадь раздела фаз

d - толщина диффузионного слоя

D - коэффициент диффузии равный:

D = D₀exp(-E/RT)

Тогда можно записать, что V = k(t)* exp(-E/RT)

Если взять два опыта с одинаковой концентрацией кислорода и в момент с одинаковой степенью протекания то k₁ = k₂, и следовательно можно записать два уравнения с двумя неизвестными

V₁ = k * exp(-E/RT)

V₂ = k * exp(-E/RT)

можно посчитать энергию активации.

1 E = 21000.

2 E = 26000.

3 E = 27000.

4 E = 28000.

Вариант 1

Опыт 1 температура - 1400 K конц. O₂ - 0.083

Опыт 2 температура - 960 K конц. O₂ - 0.040

Опыт 3 температура - 960 K конц. O₂ - 0.083

Время,час 0 1 2 3 4 5 6

Масса,гр 1,00002 1,00022 1,00033 1,00040 1,00044 1,00050 1,00056

Масса,гр 1,00002 1,00011 1,00015 1,00019 1,00022 1,00023 1,00025

Масса,гр 1,00000 1,00015 1,00022 1,00027 1,00029 1,00034 1,00037

Вариант 2

Опыт 1 температура - 1700 K конц. O₂ - 0.086

Опыт 2 температура - 960 K конц. O₂ - 0.034

Опыт 3 температура - 960 K конц. O₂ - 0.086

Время,час 0 1 2 3 4 5 6

Масса,гр 1,00002 1,00019 1,00026 1,00030 1,00035 1,00041 1,00044

Масса,гр 1,00002 1,00005 1,00008 1,00010 1,00012 1,00012 1,.00015

Масса,гр 1,00001 1,00010 1,00014 1,00017 1,00018 1,00022 1,00023

Вариант 3

Опыт 1 температура - 1400 K конц. O₂ - 0.061

Опыт 2 температура - 1510 K конц. O₂ - 0.039

Опыт 3 температура - 1510 K конц. O₂ - 0.061

Время,час 0 1 2 3 4 5 6

Масса,гр 1,00002 1,00015 1,00022 1,00027 1,00031 1,00032 1,00036

Масса,гр 1,00000 1,00015 1,00019 1,00022 1,00026 1,00030 1,00031

Масса,гр 1,00002 1,00018 1,00022 1,00028 1,00034 1,00035 1,00039

Вариант 4

Опыт 1 температура - 1700 K конц. O₂ - 0.086

Опыт 2 температура - 1530 K конц. O₂ - 0.078

Опыт 3 температура - 1530 K конц. O₂ - 0.086

Время,час 0 1 2 3 4 5 6

Масса,гр 1,00002 1,00019 1,00026 1,00032 1,00035 1,00040 1,00043

Масса,гр 1,00002 1,00017 1,00022 1,00025 1,00029 1,00033 1,00038

Масса,гр 1,00001 1,00016 1,00023 1,00027 1,00033 1,00037 1,00039

Не нашли, что искали? Воспользуйтесь поиском: