Задание на дом. К следующему занятию принести решение данного уравнения.

Мы рассмотрели некоторые варианты задач расчета равновесий в газовых смесях. В других вариантах могут ставиться другие задачи, например, обратные задачи примеру 3, но принципы подходов к их решению в основном похожи на те, что мы рассмотрели. Т.е.:

1. Если ставится задача расчета равновесных параметров газовой смеси, уже находящейся в равновесии,и для которой какие-то параметры известны, то решение такой задачи сводится к следующему.

a. Записать уравнение (или несколько в зависимости от постановки задачи) реакции между компонентами газа.

b. Записать константу равновесия реакции

c. Выразить искомые величины через известные параметры и Кр.

d. Если данной реакции задана температура по табличным данным рассчитать стандартную энергию Гиббса (если температура не задана использовать выражение для ΔG⁰ от температуры) и далее рассчитать Кр, подставив ее значение (либо выражение через температуру) в выражение для искомых величин.

e. Решить полученное выражение относительно неизвестных параметров.

2. Если ставится задача поиска параметров равновесного состояния системык которому она придет из заданного исходного, то к равновесным соотношениям необходимо будет добавить балансовые уравнения, описывающие стехиометрические соотношения изменения количеств компонентов в процессе протекания реакций.

Тема 3. Расчеты равновесий в системах с конденсированными фазами(2 часа)

В пирометаллургии значительно чаще приходится сталкиваться не с гомогенными газовыми системами, а с многофазными гетерогенными системами, в которых присутствуют не только газ, но жидкие и твердые фазы. Поэтому, приобретение навыков проведения термодинамических расчетов с участием конденсированных фаз, безусловно, является важным элементом подготовки студентов, как базовой теоретической, так и практической, поскольку даже простейшие термодинамические расчеты часто позволяют оценить принципиальную возможность протекания того или иного физико-химического процесса.

Данное занятие посвящено рассмотрению типовых задач по расчету равновесных параметров в системах с конденсированными фазами.

Рассмотрим случай, когда все участвующие в реакции конденси­рованные фазы представляют собой вещества, которые не обра­зуют друг с другом растворов, и, таким образом, только газовая фаза может быть раствором. К числу таких реакций относятся, например, следующие:

СаСO₃(т) = СаО(т) + СO₂(г); Kp = Pco₂

FеС1₂(т) + 2Н₂(г) = Fе(т) + 2НС1(г); Kp = P²_HCl/P²_H2

Многие задачи термодинамических расчетов для систем с конденсированными фазами могут быть решены с использованием известного (см. выше) закона Гульдберга и Вааге. В отличие от систем, состоящих только из идеального газа, в выражение данного закона (Кр) входят не только парциальные давления газовых компонентов газовой фазы, но и активности компонентов конденсированных фаз. Для определения активности компонентов в конденсированных фазах используют прямые экспериментальные данные или расчеты с использованием различных моделей растворов.

В классической термодинамике такая связь между различными функциями выражалась при помощи уравнения состояния. Это уравнение, однако, нецелесообразно использовать для описания жидких и твердых растворов. Таким образом, применительно к реальным растворам задача состоит в том, чтобы по любому свойству иметь возможность предсказать все остальные. При этом возникает вопрос, какую характеристику раствора принять за основную. Такая характеристика должна удовлетворять следующим требованиям:

1. через нее должны просто выражаться все термодинамические свойства растворов;

2.в предельных случаях (для идеальных растворов) она должна совпадать с концентрацией, а в реальных растворах показывать степень их отклонения от идеальности;

3. с ее помощью желательно сохранить форму уравнений, выражающих законы идеальных растворов.

В ка­честве функции, связывающей свойства растворов друг с другом, Льюисом была предложена новая величина - термодинамическая активность.

Можно определить активность данного компонента в растворе как отношение давления пара этого компонента над раствором к давлению его пара в стандартном состоянии.

a_i = p_i/p_i^ст

Актив­ность пропорциональна давлению пара (р_i^ст — постоянная вели­чина) и поэтому характеризует тенденцию компонента покинуть данную фазу.

Для совершенных растворов

Р_i = р^o_iN _iили N_i=р _i/р°_i.

Сопоставление этого соотношения с уравнением (a_i) показы­вает, что активность может совпадать с мольной долей, только если р^ст_i = р^o_i. Таким образом, для растворов, близких к совер­шенным, в качестве стандартного состояния принимается чистый компонент, и в этом случае

а_i = р_i/р°_i.

Отсюда ясно, что активность компонента в растворах, близких к совершенным, всегда меньше единицы, и только для компонента, находящегося в чистом состоянии, а_i= 1. Oчевидно, что для совершенного раствора активность равна моль­ной доле. Если поведение раствора отклоняется от совершенного, то а_i≠ N _i. Степень этого отклонения определяется величиной коэффициента активности (γ_i):

a_i/ N_i=γ_i

В случае совершенных растворовγ_i = 1 и а_i= N_i. Для реаль­ных растворов коэффициент активности может быть как меньше единицы (отрицательные отклонения), так и больше ее (положи­тельные отклонения).

В теории и практике окислительных металлургических процессов достаточно часто приходится определять условия, при которых возможнагетерогенизация жидкого гомогенного расплава с выделением из него необходимо твердой или жидкой фазы. Как правило такие режимы нежелательны для металлургического процесса, поскольку приводят к нарушению его нормального хода и часто даже к его остановке. Например, во многих процессах цветной металлургии используют железосиликатные шлаки, в которых железо присутствует как в двухвалентной форме, так и в трехвалентной. При высоком окислительном потенциале системы (высоком парциальном давлении кислорода) доля Fe³⁺ в расплаве резко возрастает, то приводит к увеличению концентрации магнетита, растворимость которого в железосиликатных шлаках ограничена. Для предотвращения гетерогенизации шлака по магнетиту необходимо определение условий, при которых он (твердый магнетит) будет выделяться из шлака в виде отдельной фазы.

Задача 1.

В пирометаллургическом процессе образуется железосиликатный шлак, содержащий 35 % SiO₂, остальное оксиды железа. Определить при каком парциальном давлении кислорода в системе будет выделяться твердый магнетит. Температура 1250 °С. Активность FeO (стандартное состояние тв. чистыйFeO)=0,4.

Решение.

Запишем реакцию, по которой образуется магнетит:

3FeO + ½ O₂ = Fe₃O₄

Твердый магнетит будет выделяться из шлака при условии a_Fe3O4=1. Тогда:

При известной активности FeO необходимо найти Kp реакции.

Из Казачкова для реакций;

1. Fe_т + ½ O₂ = FeO_т; ΔG⁰₁=-263182+64.22 ^. T = -165375Дж/моль.

2. 3Fe_т + 2O₂ = Fe₃O_4т; ΔG⁰₂=-1105608+307,31 ^. T = - 637575Дж/моль

3. 3FeO_т + ½ O₂ = Fe₃O_4т;ΔG⁰₃ =ΔG⁰₂ – 3ΔG⁰₁ = -141450 Дж/моль

Тогда:

K_p3 = exp(-ΔG⁰₃/RT)=71425 и p_O2 = 4,79^.10^-8атм.

Задача 2.

Поясните, увеличится или снизится термодинамическая вероятность выделения твердого магнетита из железосиликатного шлака при снижении концентрации в нем кремнезема.

Решение.

Для ответа на этот вопрос необходимо сравнить активность магнетита в шлаках с разным содержанием кремнезема, допустим при 35 и 30 %-х его концентрации в шлаке. Предполагаем, что все остальные параметры (парциальное давление кислорода в системе, температура) в данных вариантах одни и те же.

Рассмотрим вышеприведенную реакцию образования магнетита (3). При одной и той же температуре и p_O2активность магнетита будет полностью определяться активностью FeO в шлаке. Если шлак чисто железосиликатный, т.е. состоящий из кремнезема и оксидов железа, то снижение концентрации кремнезема должно привести к увеличению концентрации оксидов железа. Поскольку активность компонента равна его мольной доле, умноженной на коэффициент активности, то при постоянном значении последнего увеличение концентрации компонента ведет к росту его активности. Тогда из реакции (3) следует, что активность магнетита также возрастет.

Ответ. При уменьшении концентрации кремнезема в шлаке вероятность выделения твердого магнетита возрастает.

Задача 3. Поясните, увеличится или снизится термодинамическая вероятность выделения твердого магнетита из железосиликатного шлака при снижении температуры.

Решение.

Для ответа на этот вопрос необходимо сравнить активность магнетита при разных температурах. Ответ на данный вопрос требует задания некоторых других условий. Принимаем, что активность FeO и p_O2при изменении температуры не меняются (вообще говоря, это не совсем так, но расчеты этих изменений достаточно сложны). Тогда ответ на данный вопрос будет прямо связан с влиянием температуры на константу равновесия реакции (3). Для температуры 1250 °СKp рассчитана выше. Рассчитаем Kp для T=1200 °С.

1. Fe_т + ½ O₂ = FeO_т; ΔG⁰₁=-263182+64.22 ^. T = -168586Дж/моль.

2. 3Fe_т + 2O₂ = Fe₃O_4т; ΔG⁰₂=-1105608+307,31 ^. T = - 652940Дж/моль

3. 3FeO_т + ½ O₂ = Fe₃O_4т;ΔG⁰₃ =ΔG⁰₂ – 3ΔG⁰₁ = -147183 Дж/моль

Тогда:

K_p3 = exp(-ΔG⁰₃/RT)=166725

Полученное при 1200 °С значение константы равновесия более чем в два раза превышает ее значение при 1250 °С. Это значит, что при прочих равных условиях при снижении температуры активность магнетита возрастет более чем в два раза, т.е. вероятность гетерогенизации шлака по магнетиту существенно увеличится.

Ответ. При снижении температуры шлака вероятность выделения твердого магнетита возрастает.

Задача 4. Определить термодинамическую активность и коэф­фициент активности закиси меди в черновой меди, содержащей при 1423° К 0,5% (по массе) кислорода.Равновесное давление О₂ над металлом составляет 9,08∙10^-9атм; коэффициент активности меди в расплаве γ_Cu принять равным 1,0. Константа равновесия реакции окисления меди:

2Cu + 1/2O₂ = Cu₂O; K_p= a_Cu2O /a²_Cu ∙ p^1/2_O2; a_Cu2O = K_p∙ a²_Cu ∙ p^1/2_O2

В восстановительных процессах выделение магнетита из шлаков металлургов не волнует, однако, возникают другие проблемы. В частности, при восстановительном обеднении шлаков или в процессах восстановительно-сульфидирующей плавки окисленных никелевых руд при определенных условиях возникает опасность выделения в системе тугоплавкой металлической фазы на основе железа.

Задача 5.

При восстановительно-сульфидирующей обработке оксидного расплава при плавке окисленной никелевой руды решили поддерживать соотношение расходов восстановителя (топлива) и кислородсодержащего дутья таким, чтобы в отходящих газах отношение CO/CO₂ = 6. Температура процесса 1450 °С. Считаем, что отходящие газы и конденсированные продукты находятся в равновесии. Шлак железосиликатный (FeO-SiO₂). Содержание кремнезема 45 вес. %. В расчетах принять, что шлак является совершенным раствором. Определить, будет ли выделяться твердое металлическое железо в этих условиях.

Решение.

Для ответа на этот вопрос необходимо определить активность твердого железа в системе. Запишем реакцию:

Fe_т + ½ O₂ = FeO_т; ΔG⁰₁=-263182+64.22 ^. T = -152531Дж/моль.

Kp=exp(-ΔG⁰/RT)=42319

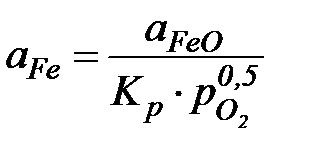
Для определения активности железа необходимо знать p_O2и активность FeO_т.

Для определения парциального давления кислорода в системе воспользуемся реакцией:

CO + ½ O₂ = CO₂; ΔG⁰=-282695+87,585 ^. T = -131786Дж/моль

Kp=exp(-ΔG⁰/RT)=9938; p_O2 = (p_CO2/K_p/p_CO)² = 2,81 ^. 10^-10атм.

Активность FeOрассчитываем, используя свойства совершенных идеальны растворов, согласно которым:

a_FeO=N_FeO

Тогда:

Ответ. Нет. Выделяться металлическое железо не будет

Замечание. Необходимо отметить, что мы рассчитывали условия выделения чистого металлического железа. Реально выделяется раствор на основе Fe, в котором активность Fe меньше единицы (зависит от состава металлической фазы). Поэтому металлическая фаза начинает выделяться уже при a_Fe<1. Для точного расчета необходимо знание активностей металлической фазы от ее состава (это же относится и к шлаку) и решать общую задачу поиска условий минимума суммарной энергии Гиббса системы, однако, эта задача не для студенческих расчетов.

Студентам на дом. Рассчитать при каком соотношении CO/CO₂ в рассматриваемых условиях начнет выделяться металлическая фаза. Принимаем, что в шлаке содержится 45 вес. % SiO₂, 15 вес. % CaO, 10 % MgO, остальное FeO.

Тема 4. Диаграммы фазовых равновесий и их применение в металлургии. Основные бинарные и тройные диаграммы состояния оксидных и сульфидных систем(2 часа)

Пирометаллургические процессы цветной металлургии осуществляются в сложных гетерогенных системах, включающих различные фазы. Важное значение при этом приобретает вопрос: какое максимальное число фаз при заданных внешних условиях (температура, давление) может находиться в равновесии, в каком направлении при заданных внешних условиях будет развиваться реакция. На эти вопросы ответ дает Правило фаз Гиббса.

Фазой (Ф) называется совокупность телесных объектов, имеющих определенный химический состав и термодинамические свойства, отделенная от других фаз поверхностью раздела. Более кратко можно определить фазу как однородную часть неоднородной системы, которая может быть извлечена из системы каким-либо механическим способом.

Числом компонентов (К) называется число индивидуальных веществ, входящих в систему, за вычетом числа химических уравнений, связывающих эти вещества. Вообще в системах без химических превращений число ком­понентов равно числу индивидуальных веществ.

Числом степеней свободы (С) называется число параметров (Т, р, концентрации), которые полностью определяют состояние системы при равновесии, или, иначе говоря, число параметров, которые можно менять в определенных пределах без изменения числа и природы фаз.

С = К + 2 - Ф

Уравнение является выражением правила фаз. Оче­видно, число степеней свободы не может быть меньше нуля, поэтому из уравнения следует, что К + 2 ≥ Ф, т. е. число фаз при равновесии не может превышать К + 2.

При наличии двух фаз, например воды и пара, число степеней свободы С = 1 +2 - 2 = 1. Теперь можно также ответить на вопрос о максимальном числе фаз, которое может одновременно существовать в двухкомпонентных, трехкомпонентных и вообще н многокомпонентных системах. Так, для двухкомпонентных систем оно равно четырем (0 = 2 + 2 - Ф), для трехкомпонент­ных - пяти (0 = 3 + 2 - Ф) и т. д.

В большом числе практически важных случаев давление яв­ляется постоянным. Это относится, например, к большинству металлургических процессов. Для таких случаев правило фаз выражается уравнением:

С = К +1 - Ф

Задача физико-химического анализа заключается в установлении зависимости между составом и свойствами сложных систем. Экспериментально определяются такие свойства, как удельный вес, поверхностное натяжение, вязкость, магнитные, каталитические и многие другие свойства.Для металлургии и металловедения представляет особый интерес в качестве основного свойства выбрать температуры плавления или температуры равновесия между жидкой и твердой фазами, а также температуры фазовых равновесий в твердом состоянии (при полиморфных превращениях, образовании и распаде твердых растворов).

Рассмотрим основные диаграммы равновесий (или состояний) и двухкомпонентных системах.

Первый тип диаграмм. КомпонентыА и В неограниченно взаимно растворимы в жидком состоянии, а в твердом состоянии не образуют ни растворов, ни химических соединений.

Горизонталь Т_ЕТ_Е называется линией с о л и д у с а, так как при более низких температурах существуют только твердые фазы, а жидкость полностью исчезает. Линии Т₁Е и Т₂Е назы­ваются линиями ликвидуса, так как при температу­рах, лежащих выше этих линий, существует только жидкая фаза.

При помощи диаграмм равновесия можно определить соотно­шение между весовыми количествами сосуществующих фаз для сплава данного состава при данной температуре. Используемое для этого правило рычага может быть пояснено рис.

Для сплава состава 1 при температуре Т₁ отношение массы жидкости Q (ж) к массе выделившихся кристаллов компонента А - Q (т) равно отношению отрезков Т₁b₁ и b₁l₁:

Q (ж) / Q (т) = Т₁b₁/b₁l₁

Второй тип диаграмм. Компоненты А и В неограниченно растворимы друг в друге как в жидком, так и в твердом состоя­нии и не образуют между собой химических соединений.

Третий тип диаграмм. КомпонентыА и В имеют ограниченную взаимную растворимость в твер­дом состоянии.

Для таких систем возможны два случая:

1.Твердые растворы образуют эвтектику, т. е. точка нонвариантного равновесия Е лежит ниже температуры плавления чистых компонентов.

2. Твердые растворы с перитектикой - нонвариантная точка Р лежит между температурами плавления чистых компонентов.

В сплавах 2, 3, 4 при охлаждении сначала кристаллизуется твердый раствор α. При понижении температуры до некоторого значения Т_Р этот раствор претерпевает превращение, которое называется перитектическим. При постоянной температуре происходит реакция между α -раствором и жидкостью состава P, в результате чего образуется новая фаза - твердый раствор β состава F.

Четвертый тип диаграммы. Компоненты А и В образуют прочные химические соединения, устойчивые вплоть до температуры плавления.

Химическое соединение, образованное компонентами А и В, может содержать эти компоненты в отношениях, несколько отличающихся от соответствующих А_мВ_n, т. е. на диаграммеимеется более или менее широкая область существования однород­ной фазы на основе этого соединения, ограниченная кривыми аb, bС, Сd и dе - так называемая область гомогенности. Слева от вертикальной штриховой линии на рис. в химическом соединении имеется дефицит атомов В, а справа - атомов А.

Основными типами руд, используемых в металлургии цветных металлов, являются окисленные и сульфидные руды, представлен­ные главным образом оксидами, сульфидами и более сложными химическими соединениями (силикатами, алюмосиликатами).

Фазовые диаграммы металл-сера, металл-кислород дают наиболее полное представление о процессах взаимодействия между серой (кислородом) и металлами, о составах образующихся фаз. Сульфиды железа являются основной составляющей сульфидных руд, концентратов и штейнов. Оксиды железа в металлургии цветных металлов являются обязательными составляющими шлаков, получающихся при плавке медных, никелевых и свинцовых руд и концентратов. Взаимодействие между оксидами железа и сульфидами металлов определяет равновесное распределение ценных компонентов между продуктамиплавки.

Не нашли, что искали? Воспользуйтесь поиском: