
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Алгебраическая форма комплексного числа.
Методические рекомендации
К выполнению самостоятельной работы
Для курсантов 1 курса Морского института
Направления 26.05.06 Эксплуатация судовых
энергетических установок по дисциплине «Математические основы механики»
Мурманск
2016 г.
Оглавление.
Справочный материал по темЕ «Комплексные числа. Изображение синусоидальных функций комплексными числами». 3
1. Алгебраическая форма комплексного числа. 3
2. Тригонометрическая форма комплексного числа. 4
3. Показательная форма комплексного числа. 7
4. Изображение синусоидально изменяющейся величины вращающимся вектором. 10
5. Изображение синусоидально изменяющихся величин комплексными числами. 14
Примерный вариант и образец выполнения.. 15
Решение задачи 1. 16
Решение задачи 2. 17
Решение задачи 3. 18
Решение задачи 4. 18
Варианты контрольной работы.. 23
Справочный материал по темЕ «Комплексные числа. Изображение синусоидальных функций комплексными числами»
Алгебраическая форма комплексного числа.
Под комплексным числом z понимается выражение вида
 , (15)
, (15)
где х и у — действительные числа,
i — мнимая единица, которая определяется соотношением:
 или
или 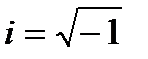 (16)
(16)
Запись (1) при этом представляет собой алгебраическую форму комплексного числа z.
Числа вида х + i0 = х отождествляются с действительными числами; в частности, 0 + i0= 0. Числа вида 0 + bi = bi называются чисто мнимыми.
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
х = Rе z, у = Iт z. (17)
Под модулем комплексного числа z понимается неотрицательное действительное число
 (18)
(18)
Сопряженным числом  к числу (1) называется комплексное число
к числу (1) называется комплексное число
 (19)
(19)
Таким образом,

и 
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
1. Пусть  и
и  .
.
Тогда 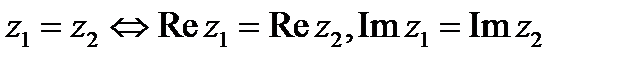 . (20)
. (20)
В частности,  .
.
2. 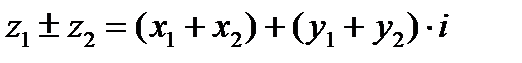 . (21)
. (21)
Отсюда следует, что
 ,
,
 .
.
3.  (22)
(22)
В случае комплексно – сопряженных чисел:
 (23)
(23)
4.  (24)
(24)
Заметим, что действия с комплексными числами в алгебраической форме производятся аналогично действиям с двучленами  и
и  с учётом соотношения
с учётом соотношения  .
.
Пример. Даны числа z 1= 4 – i и z 2 = 1 + 3 i. Вычислить  .
.
Найдем  , затем выполняем деление при помощи домножения числителя и знаменателя дроби на число, сопряженное знаменателю:
, затем выполняем деление при помощи домножения числителя и знаменателя дроби на число, сопряженное знаменателю:

(при вычислениях учтено, что  ).
).
Не нашли, что искали? Воспользуйтесь поиском: