
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Изображение синусоидально изменяющихся величин комплексными числами.
В предыдущем пункте мы рассмотрели, как синусоидально изменяющаяся величина может быть представлена проекцией на вертикальную ось вращающегося радиус-вектора. Каждый такой вектор может служить радиус-вектором комплексного числа, модуль которого равен длине вектора, а аргумент – углу, который составляет вектор с положительным направлением горизонтальной оси (рис.1).
Если колебательный процесс задан функцией  , то длина вращающегося вектора равна
, то длина вращающегося вектора равна 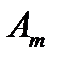 , а аргумент
, а аргумент  - текущая фаза колебаний
- текущая фаза колебаний  . Рассмотрим комплексное число, модуль которого равен амплитуде колебаний
. Рассмотрим комплексное число, модуль которого равен амплитуде колебаний 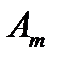 , а аргумент – фазе колебаний
, а аргумент – фазе колебаний  . Запишем это число в показательной форме:
. Запишем это число в показательной форме:
 . (42)
. (42)
По формуле Эйлера (34):

Слагаемое  представляет собой действительную часть выражения
представляет собой действительную часть выражения  :
:
 ; (43)
; (43)
а функция  представляет собой мнимую часть выражения
представляет собой мнимую часть выражения  :
:
 . (44)
. (44)
Таким образом, синусоидально изменяющуюся величину  можно представить как
можно представить как 
Рассмотрим выражение:
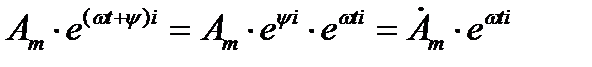 ,
,
где 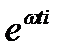 - временная составляющая - множитель, изменяющийся с течением времени, который «поворачивает» радиус-вектор на угол
- временная составляющая - множитель, изменяющийся с течением времени, который «поворачивает» радиус-вектор на угол  ;
;
 - фазовый множитель;
- фазовый множитель;
 - комплексная величина, модуль которой равен амплитуде колебаний
- комплексная величина, модуль которой равен амплитуде колебаний  , а аргумент равен начальной фазе.
, а аргумент равен начальной фазе.
Величина  называется комплексной амплитудой синусоидальной функции
называется комплексной амплитудой синусоидальной функции  . Комплексная амплитуда изображает на комплексной плоскости синусоидальную функцию а для момента времени
. Комплексная амплитуда изображает на комплексной плоскости синусоидальную функцию а для момента времени 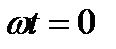 . В некоторых источниках используют знак соответствия (
. В некоторых источниках используют знак соответствия ( ):
):
 (45)
(45)
На изображении гармонических величин комплексными числами основывается символический метод расчета линейных цепей с гармоническими токами и напряжениями. Символический метод позволяет перейти от дифференциально-интегральных уравнений, описывающих линейные цепи с переменными во времени напряжениями и токами к алгебраическим уравнениям для расчета параметров комплексной схемы замещения с постоянными напряжениями и токами, что существенно упрощяет расчёты.
Замечание. В электротехнике используют иные обозначения. Чтобы не путать мнимую единицу с силой тока, вместо буквы i используют j (читается «йот»). При этом действительную ось комплексной плоскости обозначают +1, а мнимую ось + j.
Примерный вариант и образец выполнения
Контрольной работы
Задача 1. Даны два комплексных числа  . Найти
. Найти  ,
, 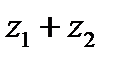 ,
,  ,
,  . Построить радиус-векторы данных чисел и результатов на комплексной плоскости.
. Построить радиус-векторы данных чисел и результатов на комплексной плоскости.
Задача 2. Даны комплексные числа  .
.
1) вычислить произведение  и частное
и частное  , используя показательную форму;
, используя показательную форму;
2) найти сумму (z1+z2) и разность (z1-z2) комплексных чисел;
3) найти приближённое значение суммы (z1+z2) и разности (z1-z2) с помощью геометрических построений.
Задача 3. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству: 
Задача 4. Даны уравнения двух колебательных процессов:
 ,
,  .
.
Необходимо:
1) построить графики колебаний и с их помощью найти графическим способом график суммарного колебания;
2) изобразить колебания при помощи векторов и графически найти вектор, изображающий суммарное колебание;
3) представить колебательные процессы комплексным числом в показательной форме и аналитически найти суммарное колебание;
4) сравнить полученные результаты.
Решение задачи 1.
Комплексных числа  заданы в алгебраической форме. Операции сложения, вычитания, умножения и деления комплексных чисел в алгебраической форме производятся по формулам (21)-(24). Получаем
заданы в алгебраической форме. Операции сложения, вычитания, умножения и деления комплексных чисел в алгебраической форме производятся по формулам (21)-(24). Получаем
 ,
,
 ,
,
 ,
,

Построим радиус-векторы данных комплексных чисел на комплексной плоскости. С помощью геометрических построений произведём операции сложения и вычитания двух радиус-векторов (рис. 8).
| Рисунок 8 |

Решение задачи 2.
Даны комплексные числа  .
.
1) вычислить произведение  и частное
и частное  , используя показательную форму;
, используя показательную форму;
2) найти сумму (z1+z2) и разность (z1-z2) комплексных чисел;
3) найти приближённое значение суммы (z1+z2) и разности (z1-z2) с помощью геометрических построений.
1) Произведение  и частное
и частное  комплексных чисел, заданных в показательной форме вычисляем по формулам (37), (38):
комплексных чисел, заданных в показательной форме вычисляем по формулам (37), (38):


2) Для нахождения суммы и разности комплексных чисел, заданных в показательной форме, необходимо перевести их в алгебраическую (15), т.к. сложение и вычитание в показательной форме не производится. Сначала, пользуясь формулой Эйлера (34), перейдём к тригонометрической форме комплексного числа. Для дальнейшего перехода к алгебраической форме вычислим значения тригонометрических функций:


Сумму и разность полученных комплексных чисел в алгебраической форме найдём по формуле (21):


Или, подсчитав приближённо,


3) Изобразим радиус-векторы данных комплексных чисел и, пользуясь правилом параллелограмма, построим вектор их суммы и вектор суммы радиус-векторов комплексных чисел  и
и  (рис. 9).
(рис. 9).
| Рисунок 9 |
 По чертежу находим действительные и мнимые части комплексных чисел z1 и z2 как проекции конца радиус-вектора на оси действительных (ОX) и мнимых значений (ОY):
По чертежу находим действительные и мнимые части комплексных чисел z1 и z2 как проекции конца радиус-вектора на оси действительных (ОX) и мнимых значений (ОY):


Сравнивая с результатами, полученными в пункте 2) делаем вывод, что геометрический метод нахождения значения суммы (z1+z2) и разности (z1-z2) комплексных чисел, представленных в показательной форме даёт достаточную для оценки результата точность.
Решение задачи 3.
| Рисунок 10 |
 Так как по определению главного значения аргумента комплексного числа:
Так как по определению главного значения аргумента комплексного числа:  , то необходимо изобразить множество точек, удовлетворяющих неравенству
, то необходимо изобразить множество точек, удовлетворяющих неравенству  . Эти точки заключены между лучами, проходящими под углами
. Эти точки заключены между лучами, проходящими под углами  и
и  радиан к положительному направлению действительной оси, причём точки, лежащие на лучах также удовлетворяют данному неравенству (рис. 10).
радиан к положительному направлению действительной оси, причём точки, лежащие на лучах также удовлетворяют данному неравенству (рис. 10).
Решение задачи 4.
1) Так как частота неизвестна, но одинакова, построим графики функций  и
и  в системе координат с горизонтальной осью ωt=х и вертикальной OY, перейдя к радианной мере значений начальной фазы:
в системе координат с горизонтальной осью ωt=х и вертикальной OY, перейдя к радианной мере значений начальной фазы:  и
и  (рис. 11).
(рис. 11).

| Рисунок 11 |

| Рисунок 12 |
Найдём суммарное колебание графическим сложением исходных колебаний. Для этого выберем произвольно точку
 на оси ОХ, найдём ординаты
на оси ОХ, найдём ординаты  и
и  соответствующих точек каждого графика исходных колебаний, найдём сумму значений найденных ординат
соответствующих точек каждого графика исходных колебаний, найдём сумму значений найденных ординат  и построим новую точку с координатами
и построим новую точку с координатами  - точку искомого графика
- точку искомого графика  . Аналогичные действия выполним для других точек горизонтальной оси (рис.12). Соединяя полученные точки синусоидой, получаем график суммы исходных колебаний
. Аналогичные действия выполним для других точек горизонтальной оси (рис.12). Соединяя полученные точки синусоидой, получаем график суммы исходных колебаний  .
.
По графику суммарного колебания определяем приближённое значение амплитуды  как наибольшего значения по оси OY.
как наибольшего значения по оси OY.
Для определения начальной фазы обращаем внимание на точки пересечения графика функции  с координатными осями. Ордината точки пересечения с осью OY отрицательна, значит значение начальной фазы также отрицательно, а значит необходимо найти абсциссу ближайшей к началу координат точки пересечения графика с осью ОХ, имеющую положительное значение. Меняя знак найденному значению абсциссы определяем начальную фазу:
с координатными осями. Ордината точки пересечения с осью OY отрицательна, значит значение начальной фазы также отрицательно, а значит необходимо найти абсциссу ближайшей к началу координат точки пересечения графика с осью ОХ, имеющую положительное значение. Меняя знак найденному значению абсциссы определяем начальную фазу:  радиан или
радиан или  .
.
 или
или 
2)
| Рисунок 13 |
 Изобразим колебание
Изобразим колебание  при помощи радиус-вектора
при помощи радиус-вектора  . Для этого в системе координат хОу построим радиус-вектор с длиной, равной 1 и под углом
. Для этого в системе координат хОу построим радиус-вектор с длиной, равной 1 и под углом  в сторону положительного направления вращения векторов, то есть против направления движения часовой стрелки. Аналогично построим радиус-вектор
в сторону положительного направления вращения векторов, то есть против направления движения часовой стрелки. Аналогично построим радиус-вектор  , соответствующий колебанию
, соответствующий колебанию  , учитывая, что угол
, учитывая, что угол  откладывается в отрицательном направлении, т.е. по движению часовой стрелки (Рис.13).
откладывается в отрицательном направлении, т.е. по движению часовой стрелки (Рис.13).

| Рисунок 13 |
 , изображающего суммарное колебание
, изображающего суммарное колебание  , воспользуемся правилом параллелограмма сложения двух векторов (рис.14). По положению полученного вектора определяем амплитуду
, воспользуемся правилом параллелограмма сложения двух векторов (рис.14). По положению полученного вектора определяем амплитуду  , измерив длину получившегося вектора и начальную фазу
, измерив длину получившегося вектора и начальную фазу  , измерив с помощью транспортира угол, который составляет получившийся радиус-вектор с положительным направлением оси Ох. Получаем суммарное колебание:
, измерив с помощью транспортира угол, который составляет получившийся радиус-вектор с положительным направлением оси Ох. Получаем суммарное колебание:  .
.
3) Для представления колебательных процессов комплексными числами в показательной форме воспользуемся переходом (45):

Тогда
 ;
;
 .
.
Чтобы найти суммарное колебание необходимо сложить два комплексных числа. Для этого перейдём в алгебраическую форму:
 ;
;
 .
.
Тогда суммарное колебание будет изображено комплексным числом

Для обратного перехода к синусоидальным функциям представим полученное комплексное число в показательной форме. Для этого вычислим значения модуля по формуле (27)

Для определения главного значения аргумента используем формулы (29). Так как комплексное число  находится в IV четверти, то
находится в IV четверти, то
 .
.
Таким образом, результирующее колебание изображается комплексным числом
 ,
,
Тогда для получения синусоидальной функции, описывающей колебательный процесс, используем формулу (44):

или, представив начальную фазу в радианах, получаем:
 .
.
4) Сравнивая полученные результаты, можем сделать вывод, что самый точный метод нахождения суммарных колебаний – использование комплексных чисел для представления синусоидальных функций. Неплохие результаты даёт использование векторной диаграммы. Работа с графиками синусоидально изменяющихся функций довольно утомительно и не даёт точных результатов.
Варианты контрольнОЙ работЫ
Каждый вариант контрольной работы для курсантов 1 курса специальности «Эксплуатация судовых энергетических установок» МГТУ содержит 4 задачи, охватывающих материал по теме «Комплексные числа. Изображение синусоидальных функций комплексными числами».
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты контрольной работы
Задача 1. Даны два комплексных числа  и
и  . Найти
. Найти  ,
, 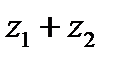 ,
,  ,
,  . Построить радиус-векторы данных чисел и результатов на комплексной плоскости.
. Построить радиус-векторы данных чисел и результатов на комплексной плоскости.
| № варианта | 
| № варианта | 
|

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задача 2. Даны комплексные числа  и
и  .
.
1) вычислить произведение  и частное
и частное  , используя показательную форму;
, используя показательную форму;
2) найти сумму (z1+z2) и разность (z1-z2) комплексных чисел;
3) найти приближённое значение суммы (z1+z2) и разности (z1-z2) с помощью геометрических построений.
| № варианта | 
| № варианта | 
|

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задача 3. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству:
| № варианта | 
| № варианта | 
|

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задача 4. Даны уравнения двух колебательных процессов:
 ,
,  .
.
Необходимо:
1) построить графики колебаний и с их помощью найти графическим способом график суммарного колебания;
2) изобразить колебания при помощи векторов и графически найти вектор, изображающий суммарное колебание;
3) представить колебательные процессы комплексным числом в показательной форме и аналитически найти суммарное колебание;
4) сравнить полученные результаты.
| № варианта |  , , 
| № варианта |  , , 
|
 , , 
|  , , 
| ||
 , , 
|  , , 
| ||
 , , 
|  , , 
| ||
 , , 
|  , , 
| ||
 , , 
|  , , 
|
Не нашли, что искали? Воспользуйтесь поиском: