
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Показательная форма комплексного числа.
Из курса математики известна формула, преобразующая показательную функцию с мнимым показателем:
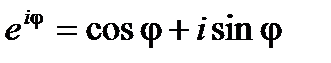 (34)
(34)
Данное равенство называется формулой Эйлера и будет более подробно рассмотрено в разделе математики «Функции комплексного переменного».
Если представить комплексное число в тригонометрической форме (28):
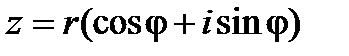
и воспользоваться формулой Эйлера (34), то получим более компактную запись:
 , (35)
, (35)
где  .
.
Полученное равенство есть показательная форма комплексного числа.
Для показательной формы, как и для тригонометрической, справедливы формулы:
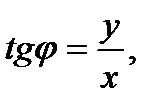
 (36)
(36)
Так как показательная форма комплексных чисел получается напрямую из тригонометрической, то действия с комплексными числами в показательной форме будут аналогичны таковым в тригонометрической форме:
1) Если  ,
, 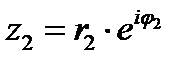 , то
, то  (37)
(37)
2) Если  ,
, 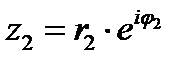 , то
, то  (38)
(38)
3) Если 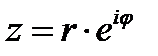 , то
, то  , где m – целое число (39)
, где m – целое число (39)
4) Если 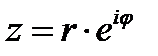 , то
, то  (40)
(40)
Замечание. Формулы (36) известны из курса математики также как формулы перехода от декартовых координат точки к её полярным координатам. Поэтому модуль r и аргумент j комплексного числа z можно рассматривать как полярные координаты точки z на комплексной плоскости. Поэтому показательную форму комплексного числа ещё называют полярной формой. Этот термин часто встречается в иностранной литературе.
При решении многих практических задач используется связь между арифметическими операциями с комплексными числами и действиями над их радиус-векторами.
Теорема 1. При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).


|

|

|
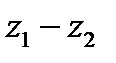
|
| Рисунок 3. |
 соответствует точке с координатами
соответствует точке с координатами  , а число
, а число  — точке с координатами
— точке с координатами  то
то 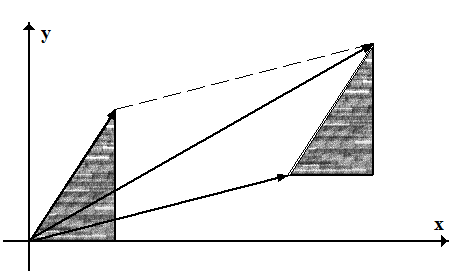

|

|
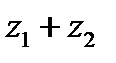
|
| Рисунок 2. |
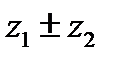 отвечает точка
отвечает точка  Так как (рис. 2) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами
Так как (рис. 2) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами  есть параллелограмм. Следовательно, радиус-вектор точки
есть параллелограмм. Следовательно, радиус-вектор точки 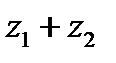 является суммой радиусов-векторов точек
является суммой радиусов-векторов точек  и
и  .
.
Теорема 2. При вычитании комплексных чисел их радиусы-векторы вычитаются.
Так как  , то
, то 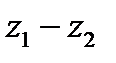 равен второй диагонали параллелограмма, построенного на векторах
равен второй диагонали параллелограмма, построенного на векторах  и
и  (рис. 3), т. е. равен разности радиусов-векторов точек
(рис. 3), т. е. равен разности радиусов-векторов точек  и
и 
Теорема 3. При домножении комплексного числа  на множитель
на множитель  радиус-вектор исходного комплексного числа поворачивается на угол
радиус-вектор исходного комплексного числа поворачивается на угол 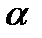 .
.
Рассмотрим произведение  . По правилу действия с комплексными числами в показательной форме (37) имеем:
. По правилу действия с комплексными числами в показательной форме (37) имеем:

Таким образом, значение аргумента полученного комплексного числа представляет собой сумму  , т.е. радиус-вектор, проходящий под углом
, т.е. радиус-вектор, проходящий под углом  к положительному направлению действительной оси перешел в радиус-вектор, проходящий под углом
к положительному направлению действительной оси перешел в радиус-вектор, проходящий под углом  , при этом длина радиус-вектора осталась неизменной, что и соответствует повороту радиус-вектора на угол
, при этом длина радиус-вектора осталась неизменной, что и соответствует повороту радиус-вектора на угол 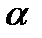 .
.
Следствие. Домножение комплексного числа на множитель i поворачивает радиус-вектор комплексного числа на 90̊ против часовой стрелки, а деление на i поворачивает радиус-вектор комплексного числа на 90̊ по часовой стрелке.
1) Представим число i в показательной форме:
 ,
,
По теореме 3 при домножении на  радиус-вектор комплексного числа повернётся на 90̊ против часовой стрелки.
радиус-вектор комплексного числа повернётся на 90̊ против часовой стрелки.
1) Рассмотрим деление произвольного комплексного числа z на i. Преобразуем частное:

Представим число  в показательной форме:
в показательной форме:
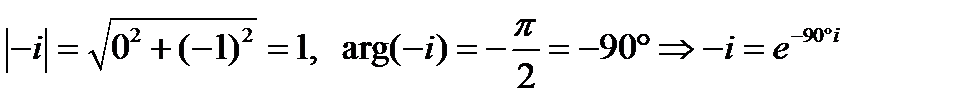 ,
,
По теореме 3 при домножении на  радиус-вектор комплексного числа повернётся на
радиус-вектор комплексного числа повернётся на  против часовой стрелки, или, иначе, на 90̊ по часовой стрелке.
против часовой стрелки, или, иначе, на 90̊ по часовой стрелке.
Не нашли, что искали? Воспользуйтесь поиском: