
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тригонометрическая форма комплексного числа.
Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, 
| z |
| Re z |
| Im z |
| φ |

|
| Рисунок 1. |
| y |
| x |
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу  может быть поставлена в соответствие точка плоскости
может быть поставлена в соответствие точка плоскости  , причем это соответствие взаимно однозначно (рис. 1), Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
, причем это соответствие взаимно однозначно (рис. 1), Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z = х + 0 = х, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + уi = уi, она носит название мнимой оси.
Заметим, что  представляет собой расстояние от точки z до начала координат.
представляет собой расстояние от точки z до начала координат.
С каждой точкой z связан радиус-вектор этой точки  ; угол, образованный радиусом-вектором точки
; угол, образованный радиусом-вектором точки 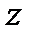 с осью Ох, называется аргументом этой точки:
с осью Ох, называется аргументом этой точки:  , причём
, причём  . Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение
. Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение  называется главным значением его и обозначается через
называется главным значением его и обозначается через  :
:
 (25)
(25)
Очевидно, что комплексно-сопряженные числа имеют одинаковые модули и противоположные аргументы:
 (26)
(26)
Примеры:  .
.
Для аргумента j из прямоугольного треугольника получаем (рис. 1):
 , где
, где  (27)
(27)
Отсюда получаем тригонометрическую форму комплексного числа:

 (28)
(28)
где  .
.
Для определения главного значения аргумента можно использовать формулы:
 (29)
(29)
Пример. Получим тригонометрическую форму комплексного числа z = – 2 – 2 i,
используя формулы (11) и (12).
 ,
,
 ,
,
следовательно, тригонометрическая форма комплексного числа z для  имеет вид:
имеет вид:
 .
.
Действия в комплексными числами в тригонометрической форме.
1. Если 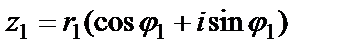 ,
,  , то
, то
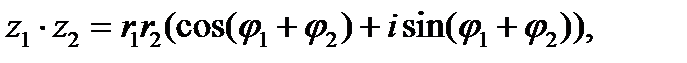 (30)
(30)
при этом в ответ записываются главные значения аргумента полученного результата, заключенные в промежутке  .
.
2. Если 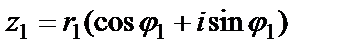 ,
,  , то
, то
 (31)
(31)
3. Если 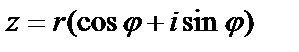 ,
,  , то
, то
 (32)
(32)
Это выражение называется формулой Муавра.
4. Если 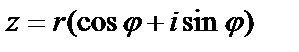 ,
,  , то
, то
 (33)
(33)
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений, при этом в ответ записываются главные значения аргумента полученного результата, заключенные в промежутке  .
.
Не нашли, что искали? Воспользуйтесь поиском: