
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Изображение синусоидально изменяющейся величины вращающимся вектором.
Любой колебательный незатухающий процесс можно представить с помощью синусоидально изменяющейся функции времени:
 , где (41)
, где (41)
Am – амплитуда колебаний – наибольшее отклонение (от среднего значения) величины, совершающей гармонические колебания.
t – время.
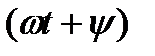 - фаза колебаний (аргумент синусоидальной функции).
- фаза колебаний (аргумент синусоидальной функции).
ψ - начальная фаза, представляет собой значение фазы в момент времени t = 0, то есть фаза, с которой начинаются колебания.
Период колебаний (Т) – время, которое проходит между повторением одинаковых фаз колебаний.
ω – угловая частота – число полных колебаний, совершающихся при периодическом колебательном процессе за 2π единиц времени. Угловая частота ω связана с периодом колебаний Т и частотой колебаний f зависимостью ω = 2πf = 2π/Т.
 Для единообразия построений графики функций с одинаковой угловой частотой
Для единообразия построений графики функций с одинаковой угловой частотой 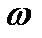 строят в системе координат с горизонтальной осью ОХ, соответствующей значениям независимой переменной
строят в системе координат с горизонтальной осью ОХ, соответствующей значениям независимой переменной 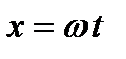 и вертикальной осью OY соответствующих значений функций. Графиком функции
и вертикальной осью OY соответствующих значений функций. Графиком функции 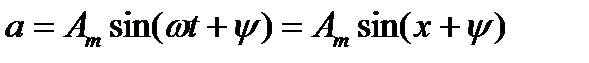 является синусоида, растянутая или сжатая в зависимости значения амплитуды
является синусоида, растянутая или сжатая в зависимости значения амплитуды 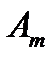 , смещённая влево на
, смещённая влево на 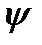 единиц, то есть точка, соответствующая началу координат, смещается в точку с координатами
единиц, то есть точка, соответствующая началу координат, смещается в точку с координатами 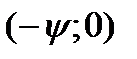 . При этом ордината точки пересечения полученной синусоиды с осью OY, очевидно, равна
. При этом ордината точки пересечения полученной синусоиды с осью OY, очевидно, равна 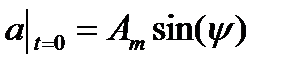 . Так как для любого угла
. Так как для любого угла 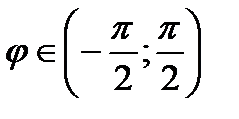 знак синуса совпадает со знаком его аргумента, то значение начальной фазы совпадает по знаку с ординатой точки пересечения с осью OY. Этот факт помогает правильно выбрать точку пересечения с осью ОХ при определении фазы.
знак синуса совпадает со знаком его аргумента, то значение начальной фазы совпадает по знаку с ординатой точки пересечения с осью OY. Этот факт помогает правильно выбрать точку пересечения с осью ОХ при определении фазы.
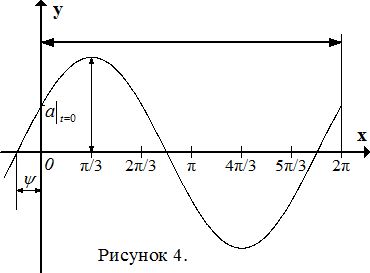
Рассмотрим для примера графически заданную синусоидальную функцию (рис.4). Для определения амплитуды колебаний 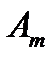 найдём наибольшую ординату графика данной функции: очевидно, для рассматриваемого примера
найдём наибольшую ординату графика данной функции: очевидно, для рассматриваемого примера 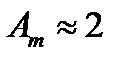 . Начальная фаза колебаний
. Начальная фаза колебаний 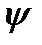 определяется с помощью одной из двух ближайших к началу координат точек пересечения графика функции с осью ОХ. В рассматриваемом примере ордината
определяется с помощью одной из двух ближайших к началу координат точек пересечения графика функции с осью ОХ. В рассматриваемом примере ордината 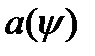 точки пересечения графика функции с осью OY положительна, тогда значение начальной фазы положительно, а значит точка пересечения графика функции с осью ОХ будет иметь отрицательную абсциссу. Таким образом, для определения начальной фазы выбираем точку пересечения графика функции с осью ОХ, лежащую левее начала координат и меняем знак её абсциссы. Получаем приближённое значение
точки пересечения графика функции с осью OY положительна, тогда значение начальной фазы положительно, а значит точка пересечения графика функции с осью ОХ будет иметь отрицательную абсциссу. Таким образом, для определения начальной фазы выбираем точку пересечения графика функции с осью ОХ, лежащую левее начала координат и меняем знак её абсциссы. Получаем приближённое значение 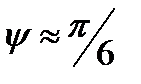 (рис. 4).
(рис. 4).
Для представления синусоидально изменяющейся величины (41) вращающимся вектором построим радиус-вектор 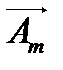 , начало которого совпадает с началом координат, длина равна амплитуде Аm, а уголк горизонтальной оси равен
, начало которого совпадает с началом координат, длина равна амплитуде Аm, а уголк горизонтальной оси равен 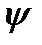 . Это будет его исходное положение в момент начала отсчета времени t = 0 (Рис. 5а).
. Это будет его исходное положение в момент начала отсчета времени t = 0 (Рис. 5а).
| а) б) Рисунок 5 |
| t |
Из конца радиус-вектора 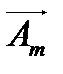 , находящегося в начальном положении, опустим перпендикуляр на горизонтальную ось. Длина этого перпендикуляра (она же проекция вектора
, находящегося в начальном положении, опустим перпендикуляр на горизонтальную ось. Длина этого перпендикуляра (она же проекция вектора  на ось ординат), равная
на ось ординат), равная 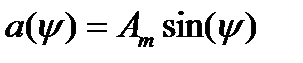 , есть мгновенное значение функции a в момент времени t = 0 (Рис. 5б).
, есть мгновенное значение функции a в момент времени t = 0 (Рис. 5б).
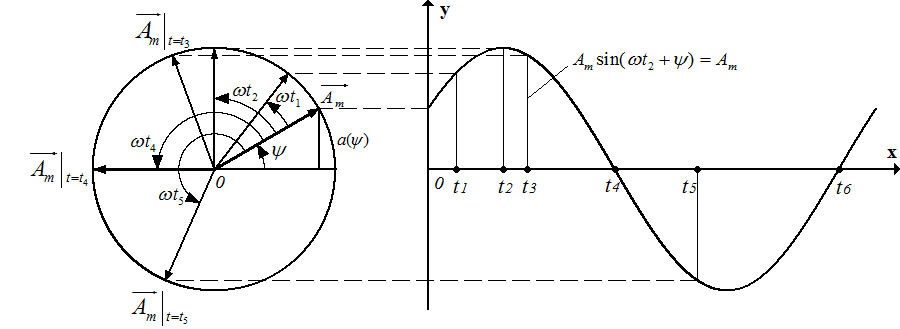
Предположим, что радиус-вектор вращается с постоянной угловой частотой ω = 2π/T = 2πf против направления движения часовой стрелки, где Т — период, f — частота вращения (частота синусоиды). Тогда один оборот вектора вокруг начала координат (поворот на 360° или 2π — в радианах) соответствует одному периоду колебаний.
В момент времени t1 радиус-вектор  будет повернут относительно начального положения на угол ωt1; длина перпендикуляра, опущенного из его конца, будет равна Am sin (ωt1+ ψ).
будет повернут относительно начального положения на угол ωt1; длина перпендикуляра, опущенного из его конца, будет равна Am sin (ωt1+ ψ).
Очевидно, длина перпендикуляра, опущенного из конца вращающегося радиус-вектора на горизонтальную ось, будет максимальной в момент времени t2, при котором ωt2+ ψ = π/2 = 90˚:
Am sin (ωt2+ ψ) = Am sin (π/2) = Аm
Рядом с окружностью, описываемой концом вращающегося радиус-вектора, можно построить в прямоугольной системе координат график зависимости синусоидальной величины  от времени t (Рис. 5б). В момент t2 синусоидальная величина а достигает максимального значения.
от времени t (Рис. 5б). В момент t2 синусоидальная величина а достигает максимального значения.
Далее, по мере вращения радиус-вектора, его проекция на вертикальную ось, т.е. синусоидальная величина  , оставаясь положительной, уменьшается, достигая нулевого значения в момент времени t4, а в следующий момент времени, например t5, мгновенное значение синусоидальной величины а получаются отрицательными, с момента t6 снова положительными и так далее.
, оставаясь положительной, уменьшается, достигая нулевого значения в момент времени t4, а в следующий момент времени, например t5, мгновенное значение синусоидальной величины а получаются отрицательными, с момента t6 снова положительными и так далее.
Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты при анализе сложной электрической цепи. Построенный для начального момента времени радиус-вектор называется векторной диаграммой синусоидального процесса.
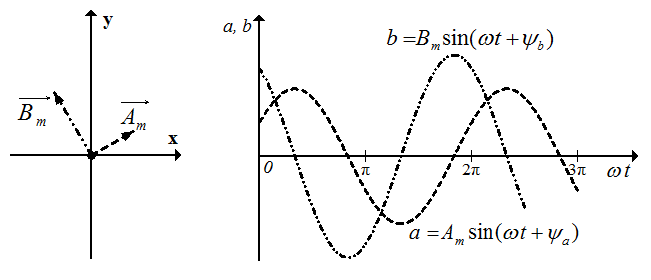
| а) б) Рисунок 6 |
Для примера, построим векторные диаграммы процессов, заданных функциями
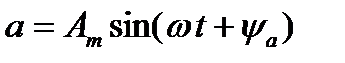 и
и 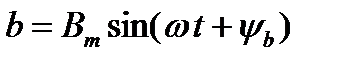 при условии, что амплитуда Bm будет в полтора раза больше амплитуды Am,
при условии, что амплитуда Bm будет в полтора раза больше амплитуды Am, 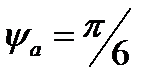 ,
, 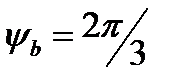 (Рис. 6а), а рядом на этом же рисунке — эти же процессы с помощью графиков функций (Рис. 6б). Очевидно, что процесс построения векторных диаграмм намного проще изображения синусоид. Кроме того, на них четко видно соотношение фаз сигналов, что является очень важной характеристикой (на Рис.6а видно, что вектор
(Рис. 6а), а рядом на этом же рисунке — эти же процессы с помощью графиков функций (Рис. 6б). Очевидно, что процесс построения векторных диаграмм намного проще изображения синусоид. Кроме того, на них четко видно соотношение фаз сигналов, что является очень важной характеристикой (на Рис.6а видно, что вектор 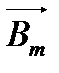 на 90° опережает вектор
на 90° опережает вектор  ), на синусоидах это определить довольно сложно.
), на синусоидах это определить довольно сложно.
Не нашли, что искали? Воспользуйтесь поиском: