Выбор независимых переменных 3 страница

т.е. , то в силу равенства (2.41) имеем

(2.42)

Это и означает, что вектор ортогонален приращению градиента . Указанное свойство позволяет сформулировать достаточно простой вычислительный алгоритм сопряжённых градиентов. Обозначим 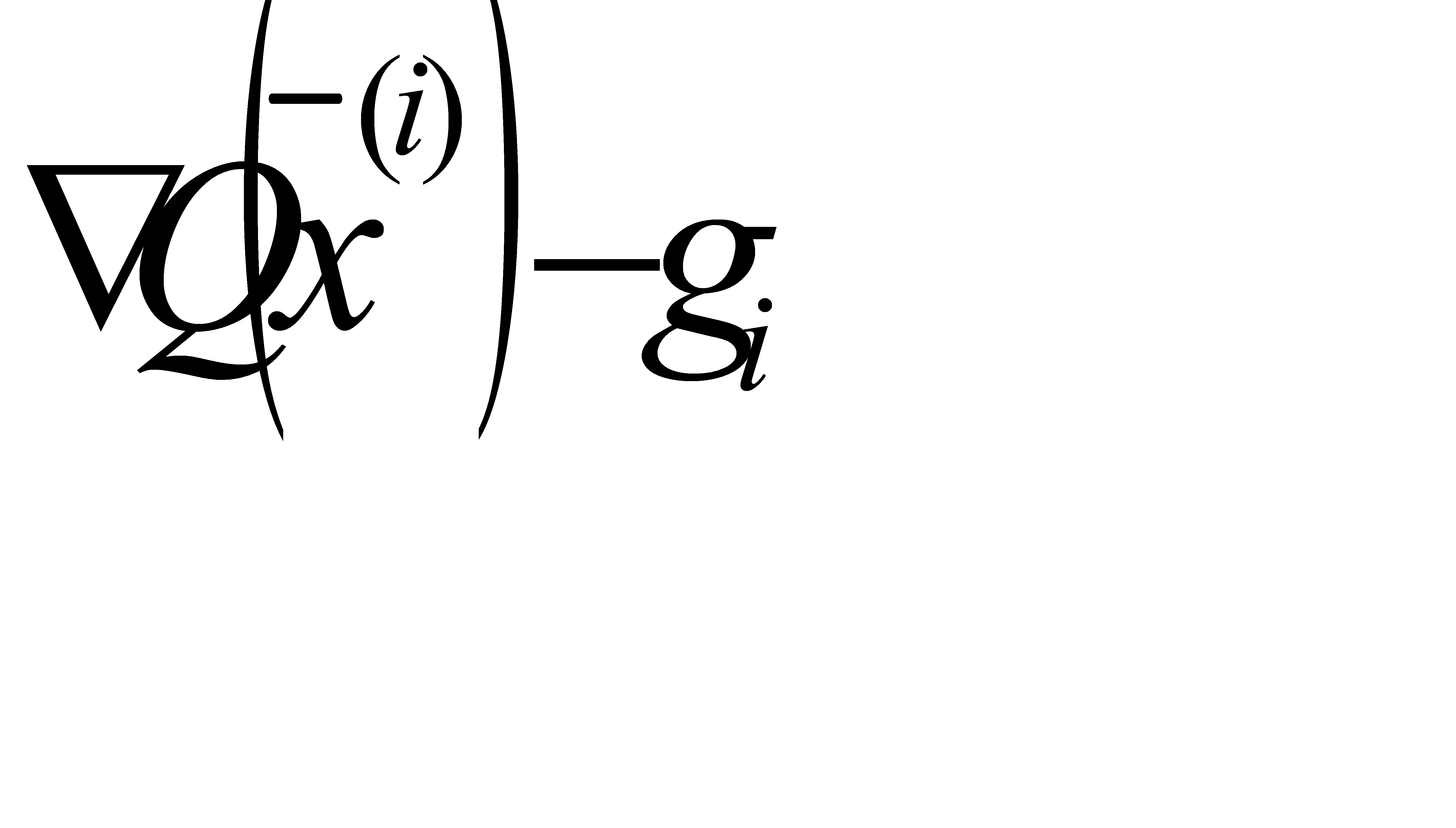. Разность градиентов в точках и обозначим

(2.43)

Начальная итерация при заданном включает вычисление градиента и поиск минимума в направлении . Обозначим точку этого минимума 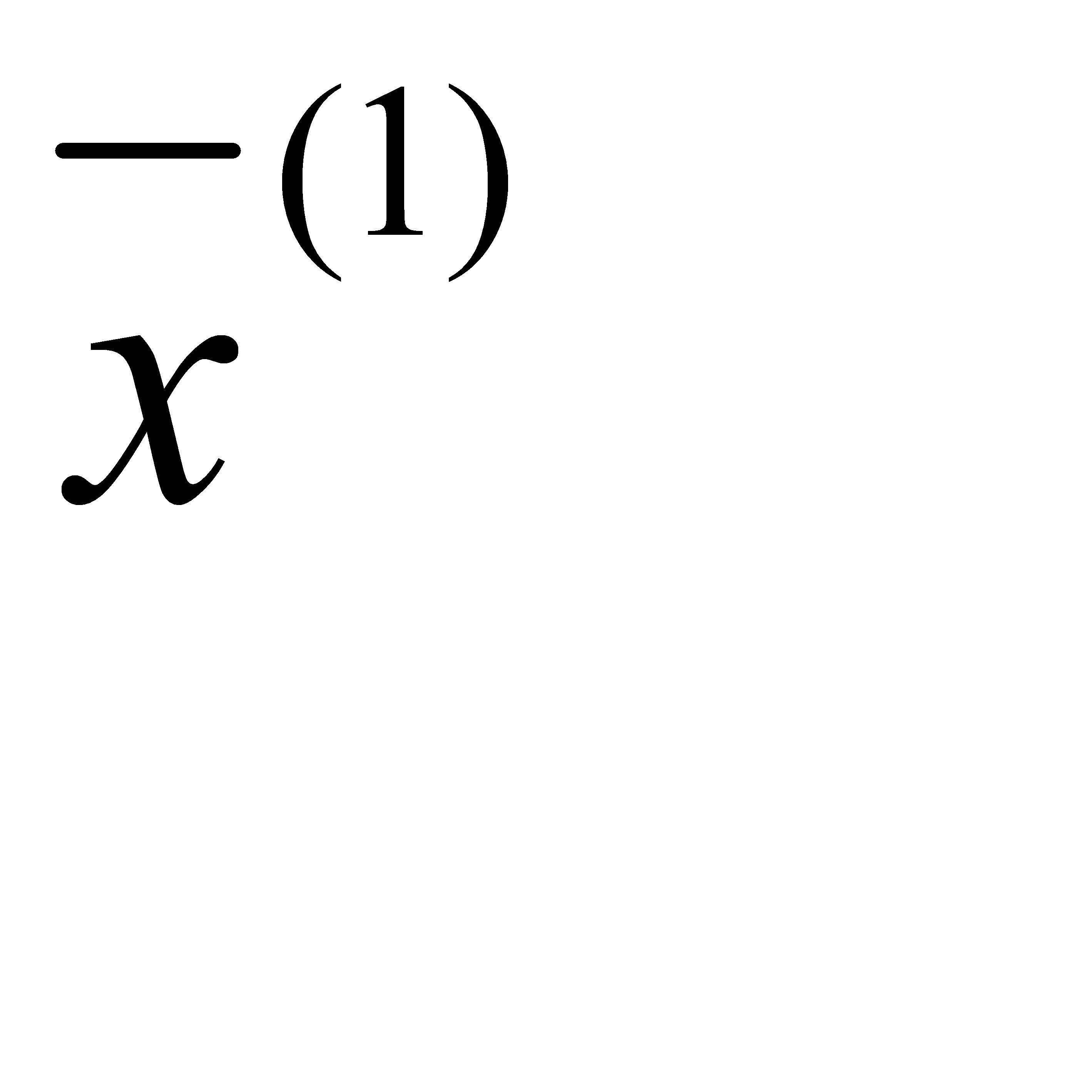и градиент в этой точке . Тогда, полагая для первого из сопряжённых направлений

(2.44)

где - неопределённый коэффициент. Он вычисляется с помощью условия сопряжённости

(2.45)

В силу того, что переход от итерации к 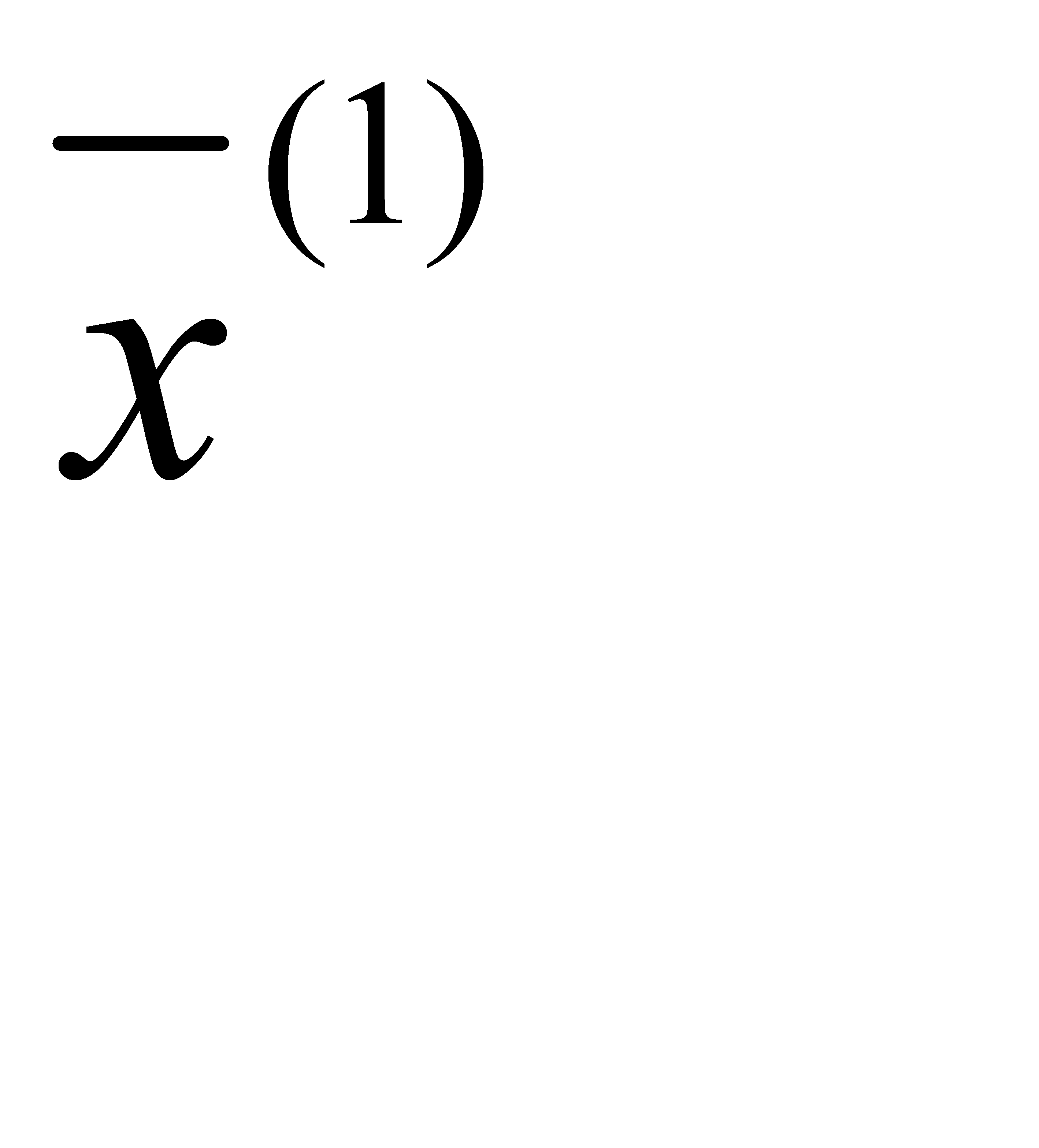совершается с помощью метода наискорейшего спуска, векторы и ортогональны. Поэтому . Отсюда

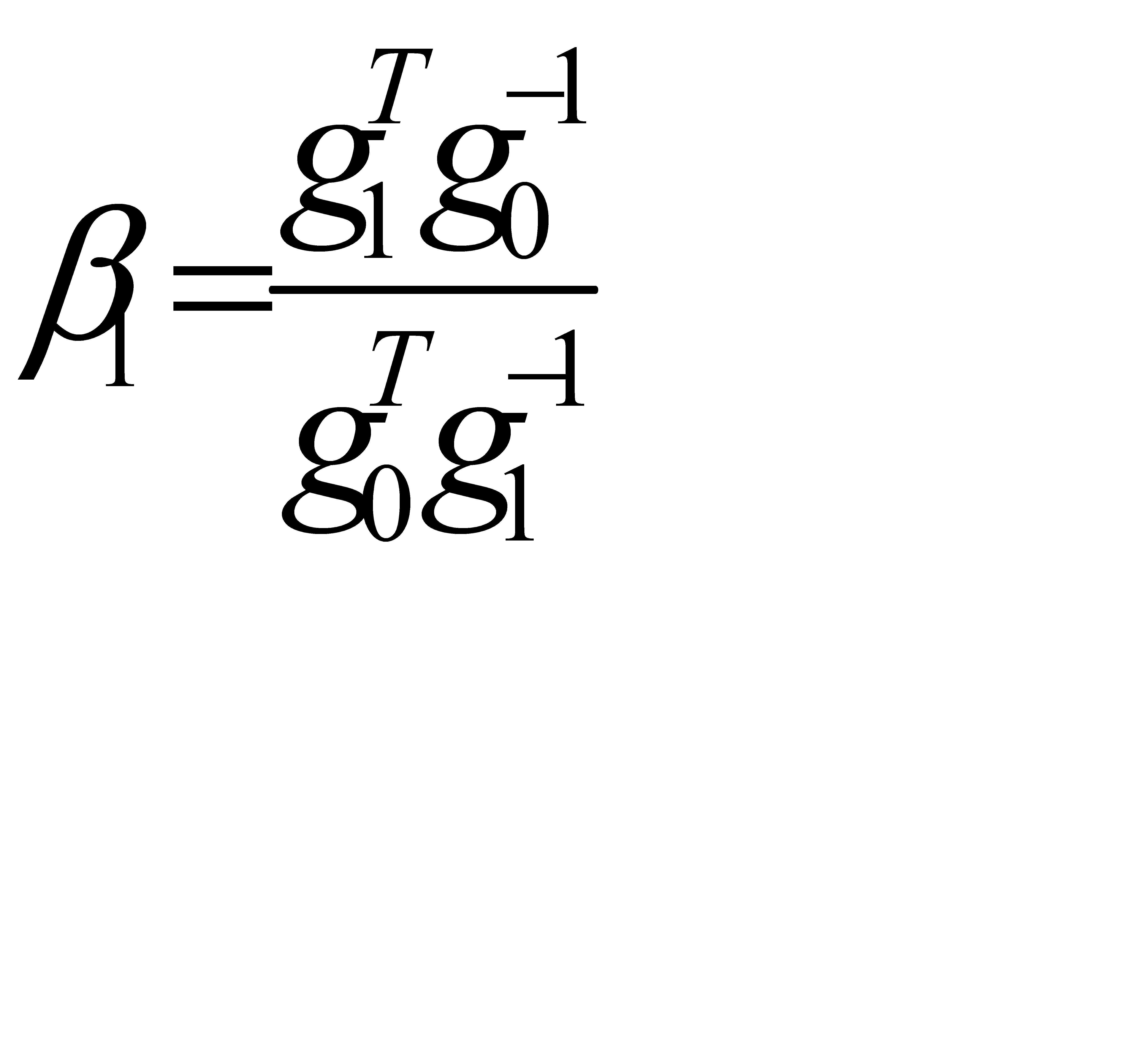(2.46)

В общем случае очередное направление поиска представляет линейную комбинацию предыдущих сопряжённых направлений

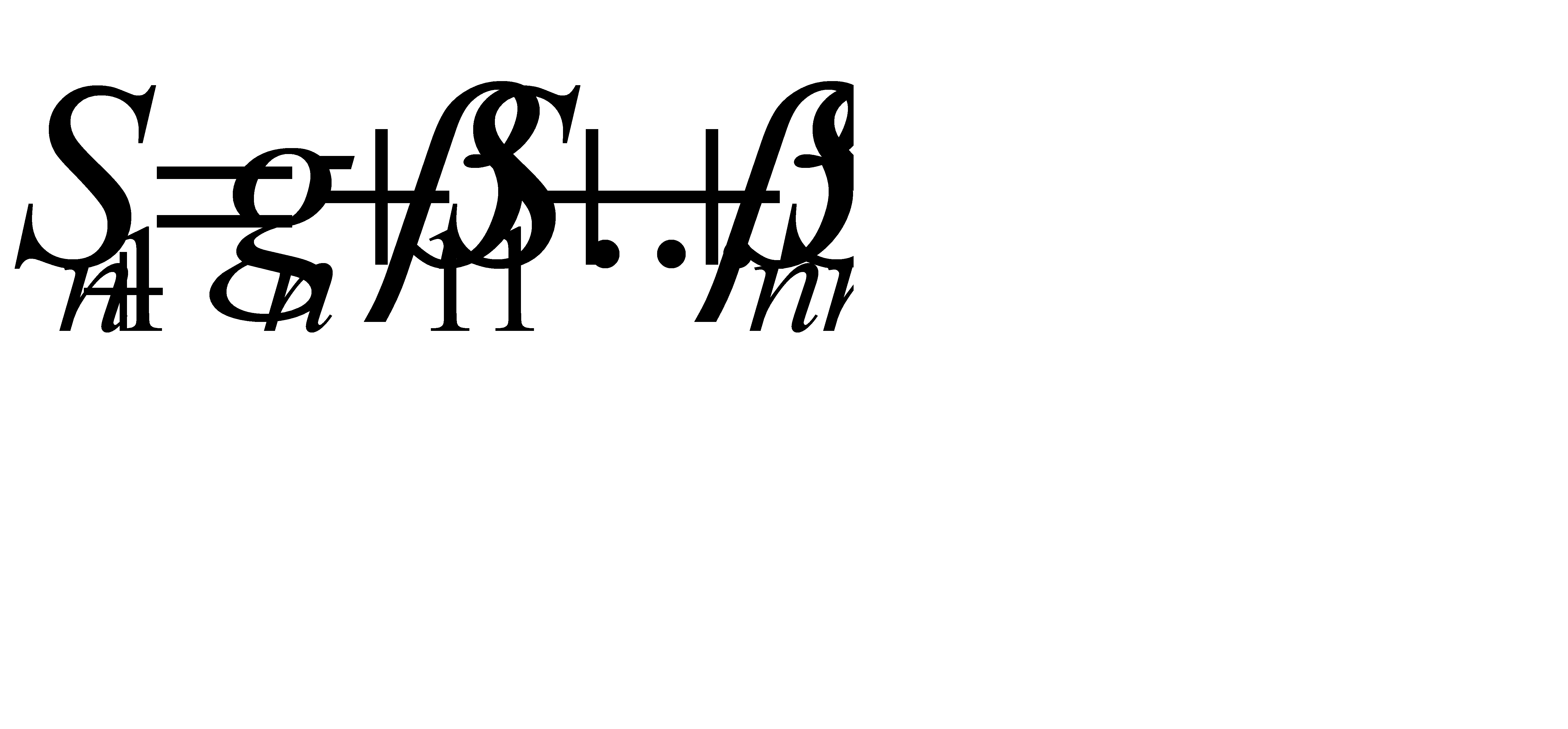, (2.47)

где .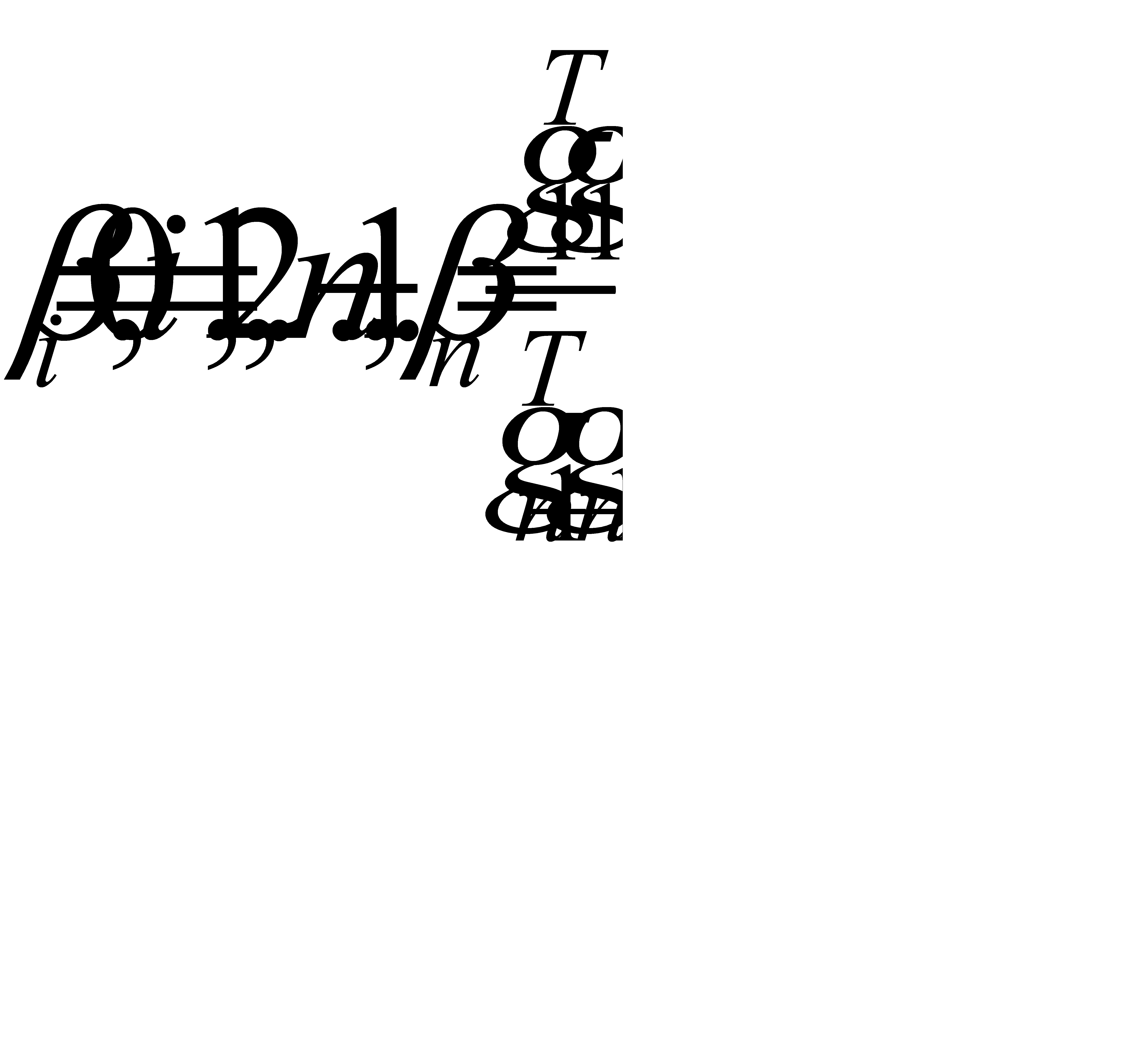

2.5 «Овражные» методы поиска

Многие трудности решения задачи НЛП связаны с ситуацией, когда поверхности уровня имеют «овражную» структуру [4, 5, 7, 43], характеризующуюся ''оврагами'' с крутизной склонов намного больше, чем крутизна образующей ''дна оврага''. В этом случае неудачный выбор начального приближения приводит к тому, что детерминированные алгоритмы либо останавливаются далеко от точки локального экстремума, либо сходятся очень медленно. Поэтому при решении многих практических задач в «овражной» ситуации используются «овражные» методы поиска, предусматривающие два этапа [4, 5, 7, 43]. На первом этапе производится поиск из близлежащих начальных точек с помощью простейших случайных алгоритмов. Полученные «оптимальные» точки расположены, как правило, по «дну оврага».

На втором этапе направление поиска определяется по двум точкам на «дне оврага» и вдоль этого направления делается овражный шаг постоянной длины. Поиск оптимума производится путём аппроксимации «дна оврага» линейной или квадратичной зависимостью.

Метод статистического градиента с адаптацией шага по распределению Джонсона (Волынский – Филатов)

Эффективность существующих алгоритмов регулярного и случайного поиска во многом зависит от выбора длины начального шага и его адаптации в процессе поиск. В работе [44] предлагается алгоритм случайного поиска с переменной длиной рабочего шага, адаптирующейся в соответствии с характером изменения функции качества. В основу алгоритма положена идея статистического градиента

(2.48)

где

- независимые случайные векторы, распределённые равномерно по единичной сфере;

- величина пробного шага на i-ой итерации.

При наличии ограничений, накладываемых на область изменения переменных в качестве закона распределения длины шага в такой области может быть использовано распределение Джонсона. Считая , запишем выражение для вычисляемого шага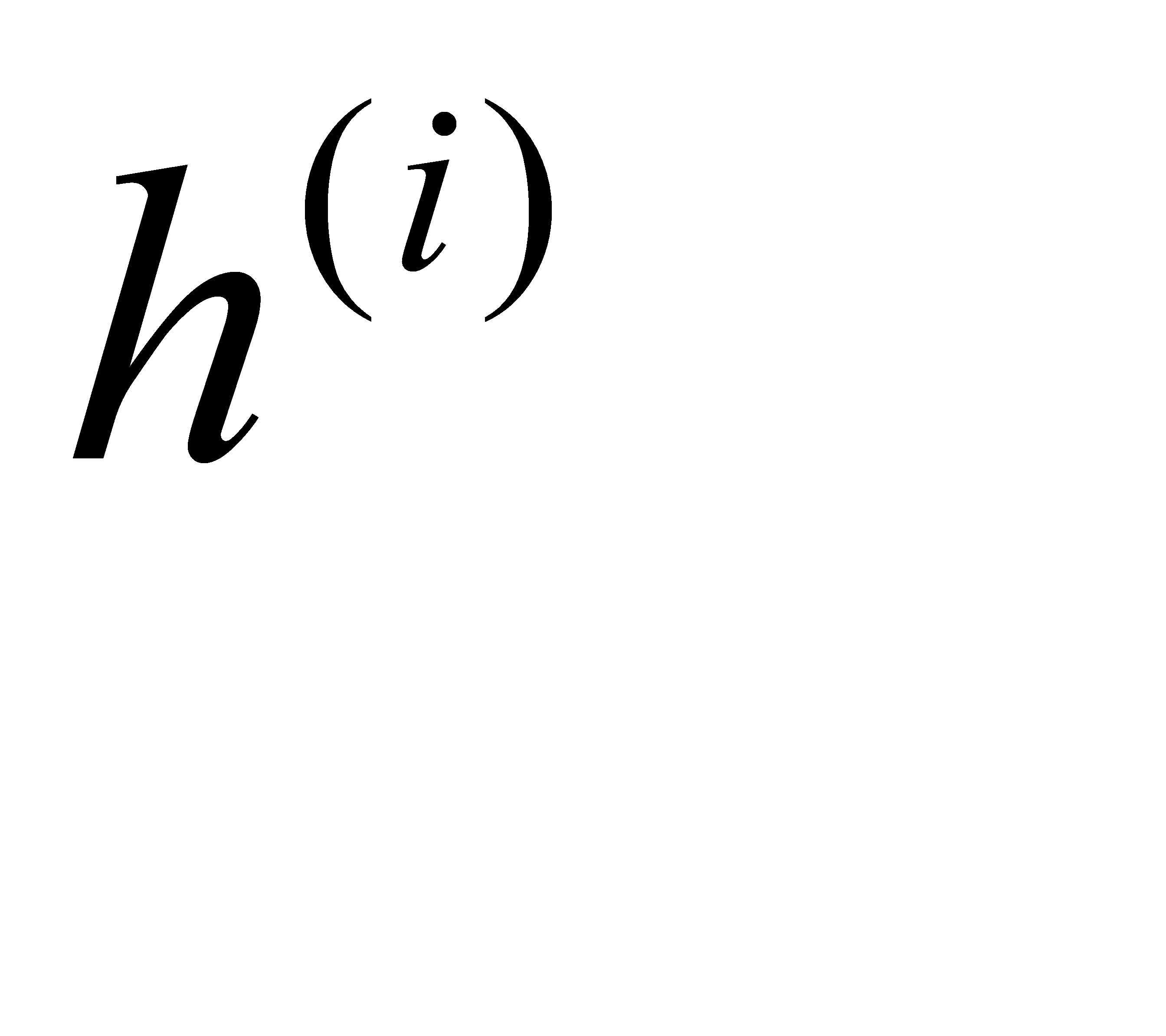

(2.49)

где - величина максимального допустимого шага;

r – нормально распределённая случайная величина с параметрами (0,1).

Изменение средней величины шага в процессе поиска происходит обучением параметра , которое осуществляется по общему правилу с забыванием

(2.50)

где - коэффициент забывания предыстории;

- коэффициент скорости обучения;

- наибольшая величина шага из серии «удачных» пробных и рабочего шагов при переходе от точки к ;

(2.51)

В процессе поиска предусматривается увеличение скорости обучения в зависимости от скорости изменения оптимизируемой функции вдоль выбранных направлений

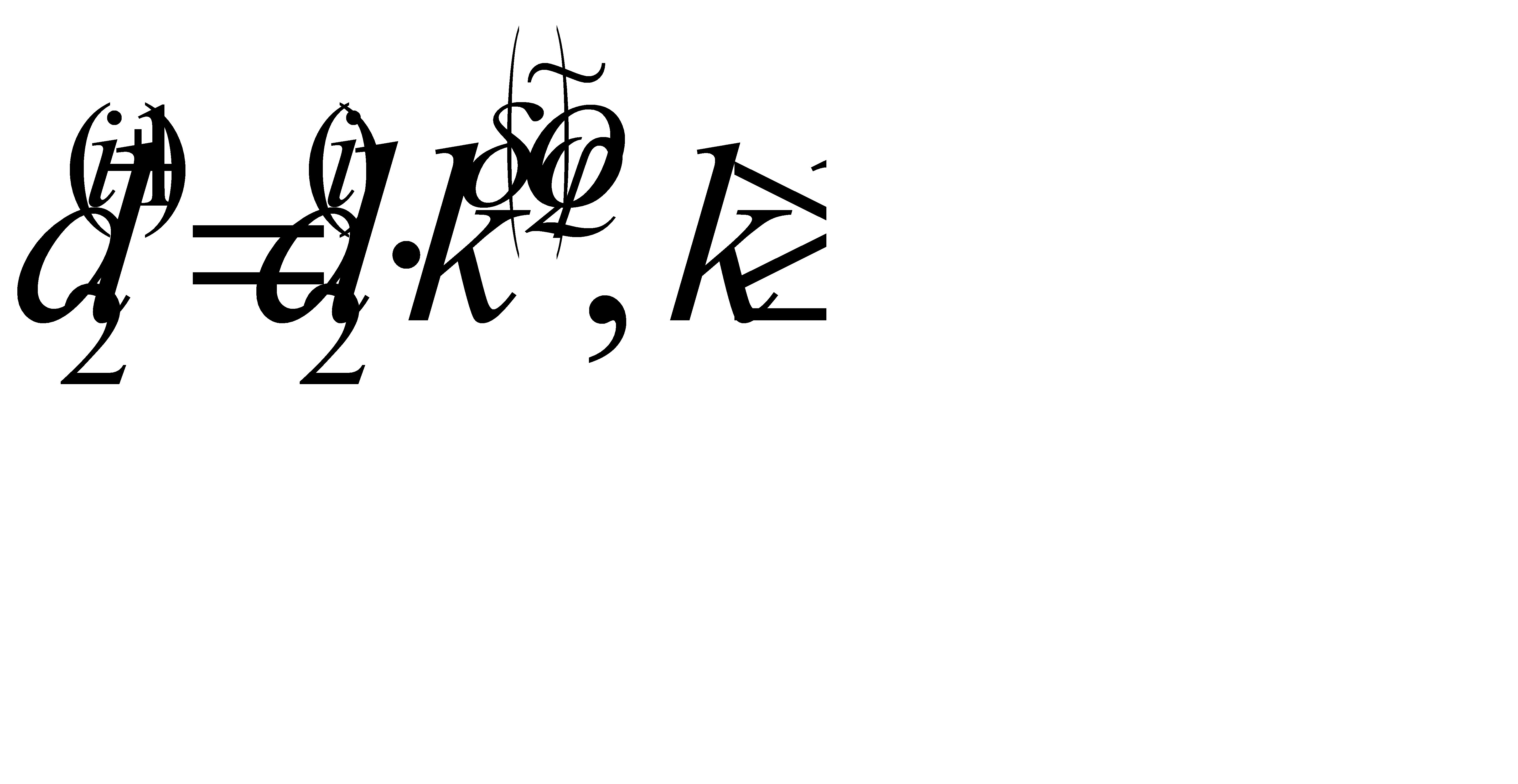(2.52)

где k – максимально допустимая величина изменения скорости обучения на одном шаге;

- наибольшее значение из серии «удачных» пробных и рабочего шагов на i -ом этапе;

φ – непрерывная функция ( для 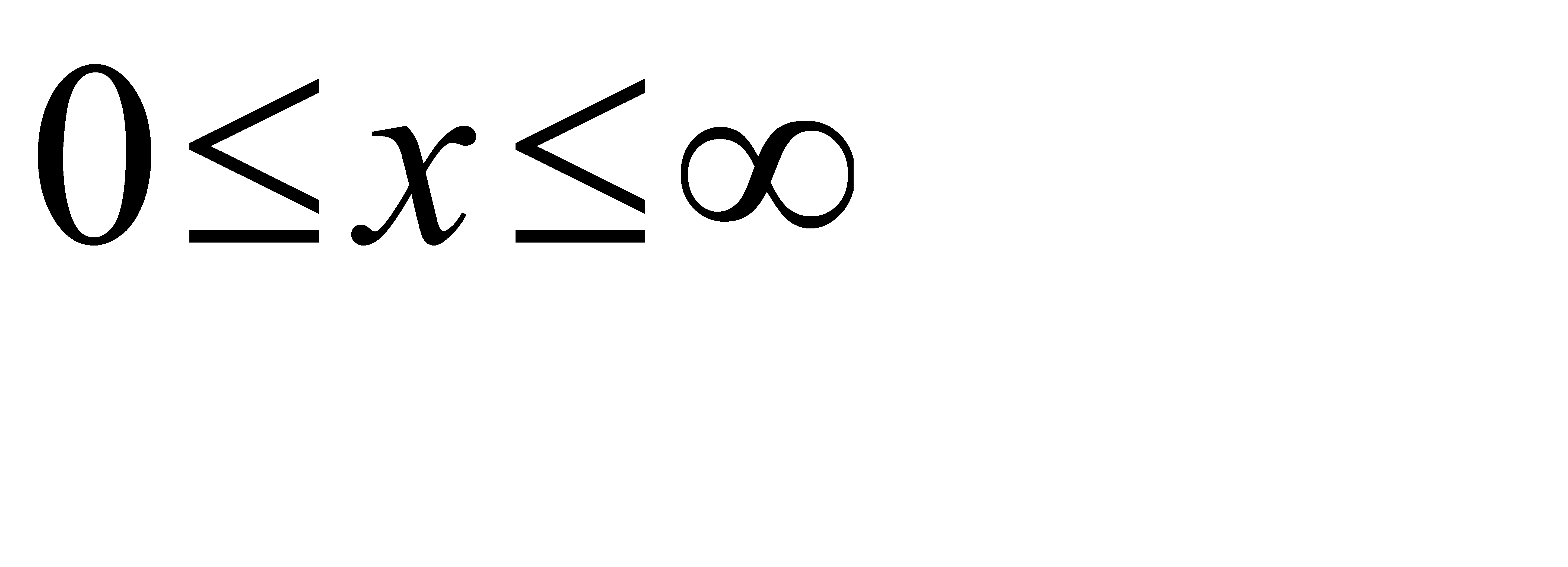), например - некоторый коэффициент.

Для сокращения потерь на поиск при попадании в район экстремума с большим шагом или в овражных ситуациях введён переходный этап поиска. Обучение параметров закона распределения длины шага на этом этапе имеет вид:

(2.53)

где а - номер шага, соответствующего началу переходного этапа.

Выражение (2.53) используется алгоритмом до тех пор, пока не будет найдено значение параметров , при котором система переместится в точку с меньшим значением критерия качества. После этого используется правило (2.50).

Предлагаемый авторами метод [44] эффективен в овражных ситуациях и в задачах с ограничениями.

В отношении выбора параметров алгоритма можно отметить следующее. Интервал изменения для можно выбирать симметричным относительно 0: , где - конечное по модулю значение , соответствующее минимальной величине шага.

В практических расчётах в зависимости от точности ε может быть выбрано в интервале от 50 до 100, но таким, чтобы σ <1: . Остальные параметры могут принимать значения

.

Метод случайного поиска с регулируемой величиной спуска, используемый в качестве овражного

Предлагаемый метод является сочетанием наиболее известных методов: случайного поиска с адаптацией шага [34] и метода наискорейшего спуска [41]. Случайный поиск с регулируемой величиной спуска объединяет достоинства исходных методов, тем самым обеспечивая более эффективный поиск широкого класса целевых функций. Суть алгоритма с регулируемой величиной спуска заключается в следующем. Он отличается от изложенных поисковых методов тем, что изменение «удачного» направления производится не на каждом шаге (как в алгоритме случайного поиска «с возвратом» с адаптацией рабочего шага) и не при нарушении условия

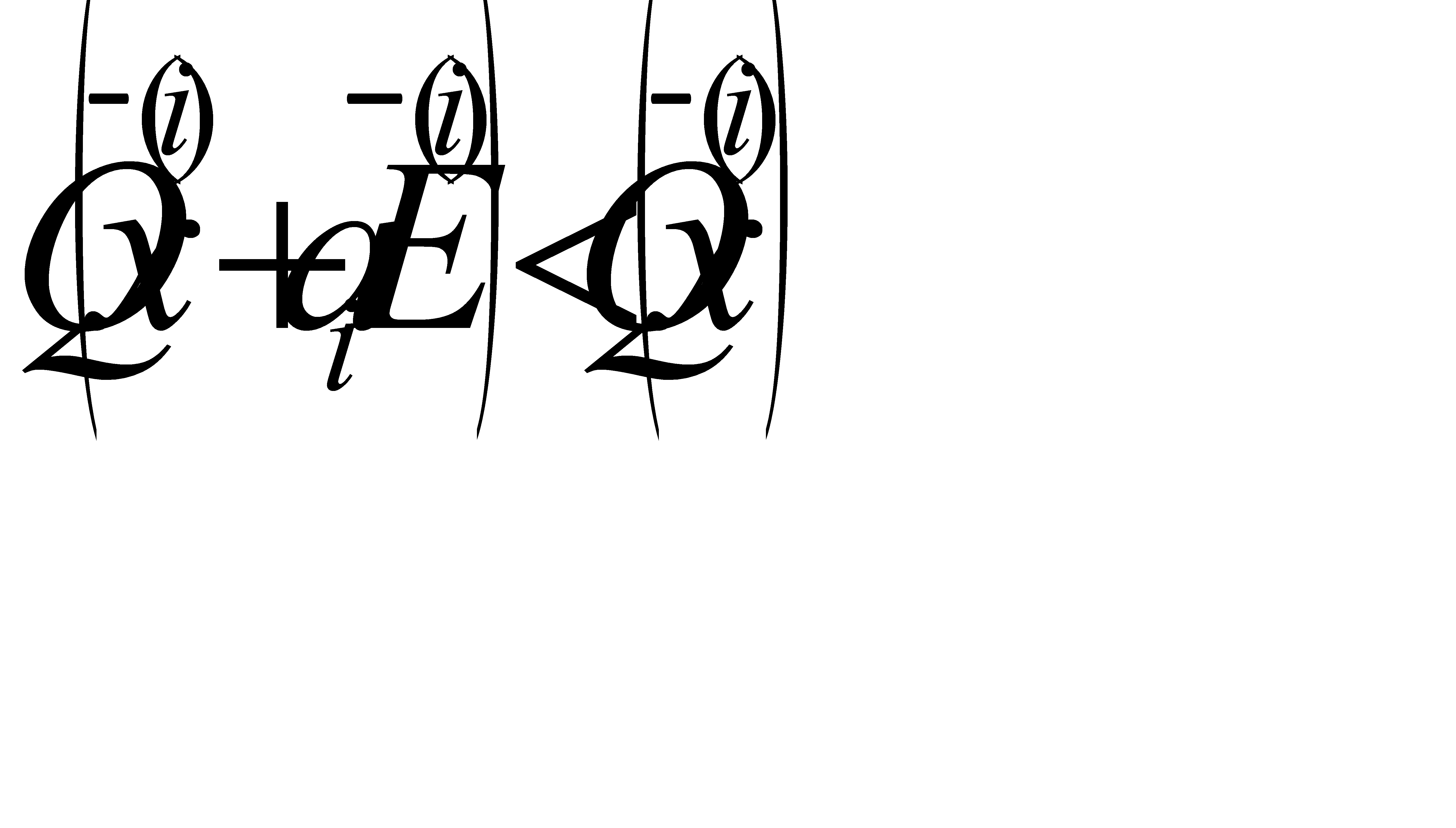(2.54)

(как в стохастическом варианте метода наискорейшего спуска), а при выполнении условия

, (2.55)

где - коэффициент спуска ().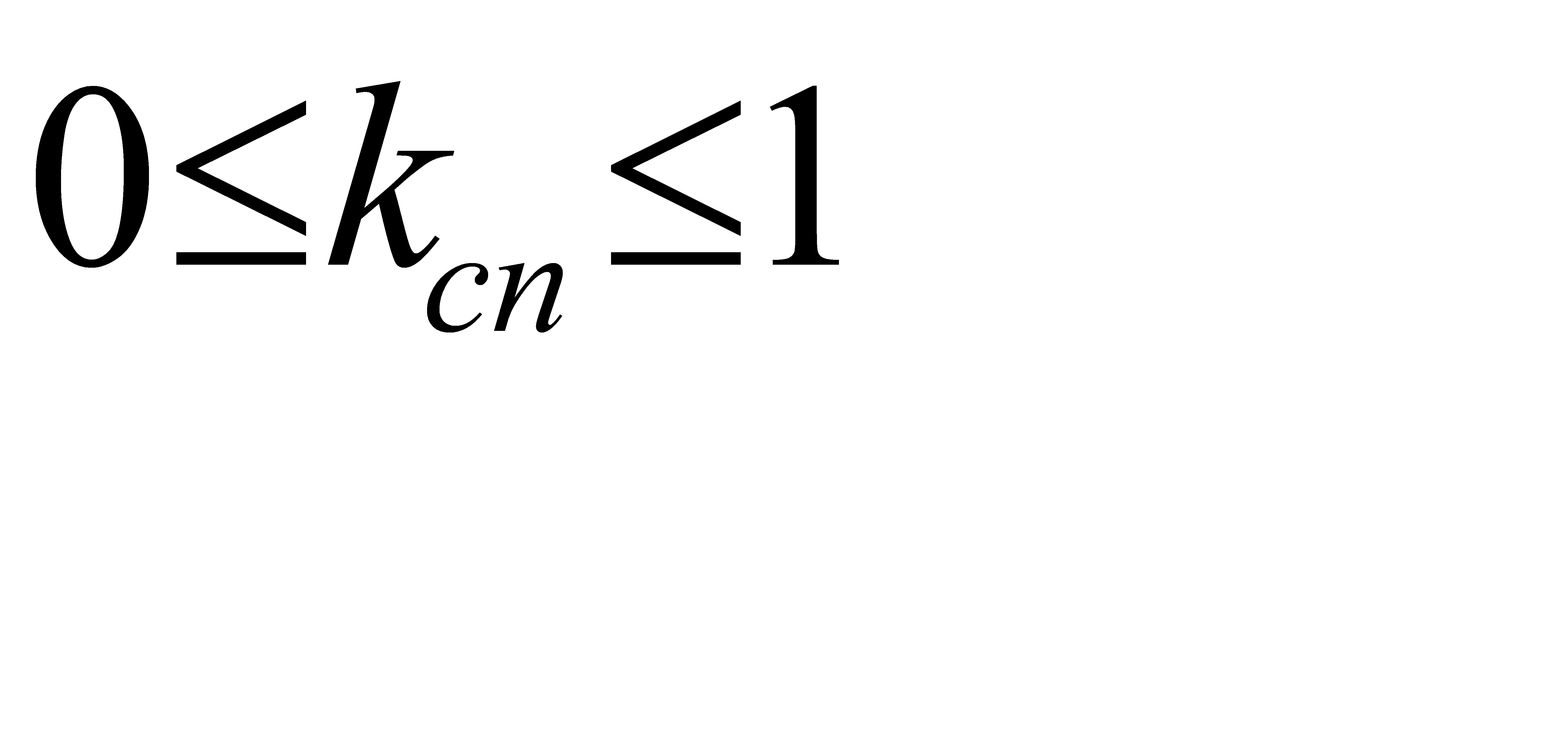

Таким образом, спуск в «удачном» направлении продолжается до тех пор, пока текущее значение целевой функции не уменьшится (при минимизации) в раз относительно величины целевой функции, полученной при первом «удачном» шаге (h =1).

Проведённые исследования показали, что при значении коэффициента спуска среднее число вычислений в алгоритме с регулируемой величиной спуска уменьшилось на 34.65% по сравнению с алгоритмом случайного поиска с адаптацией шага и на 29.97% по сравнению со стохастическим вариантом метода наискорейшего спуска. Исследования проводились на тестовой функции вида

при ограничениях имеющей экстремум при и . Кроме того, объём вычислений с увеличением r, где

в стохастическом варианте метода наискорейшего спуска возрастает значительно быстрее, чем в предлагаемом алгоритме.

Метод оврагов

В рассматриваемом методе [45] используется линейная аппроксимация «дна оврага». Пусть и 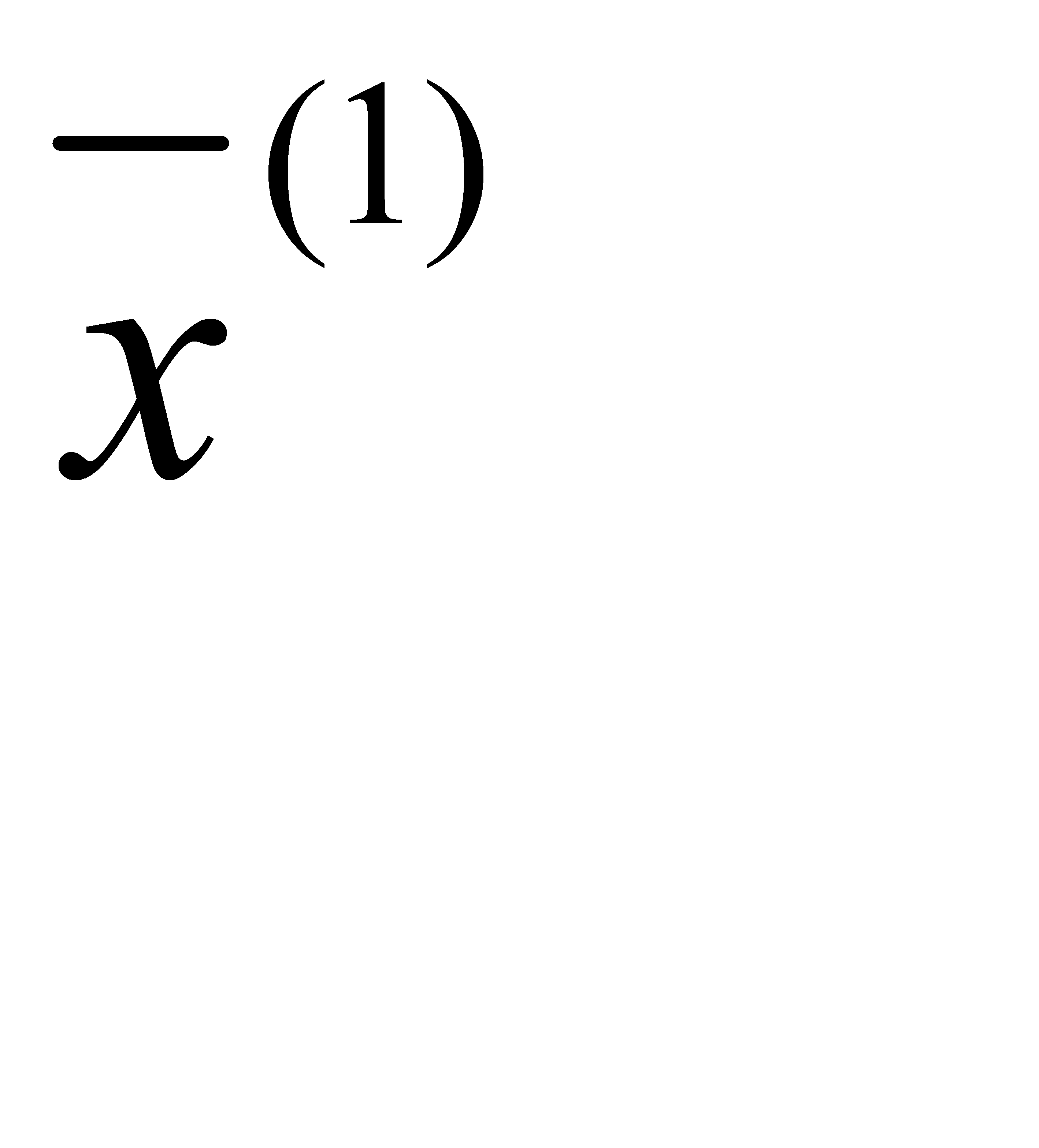- две точки на «дне оврага», причём , тогда полагают

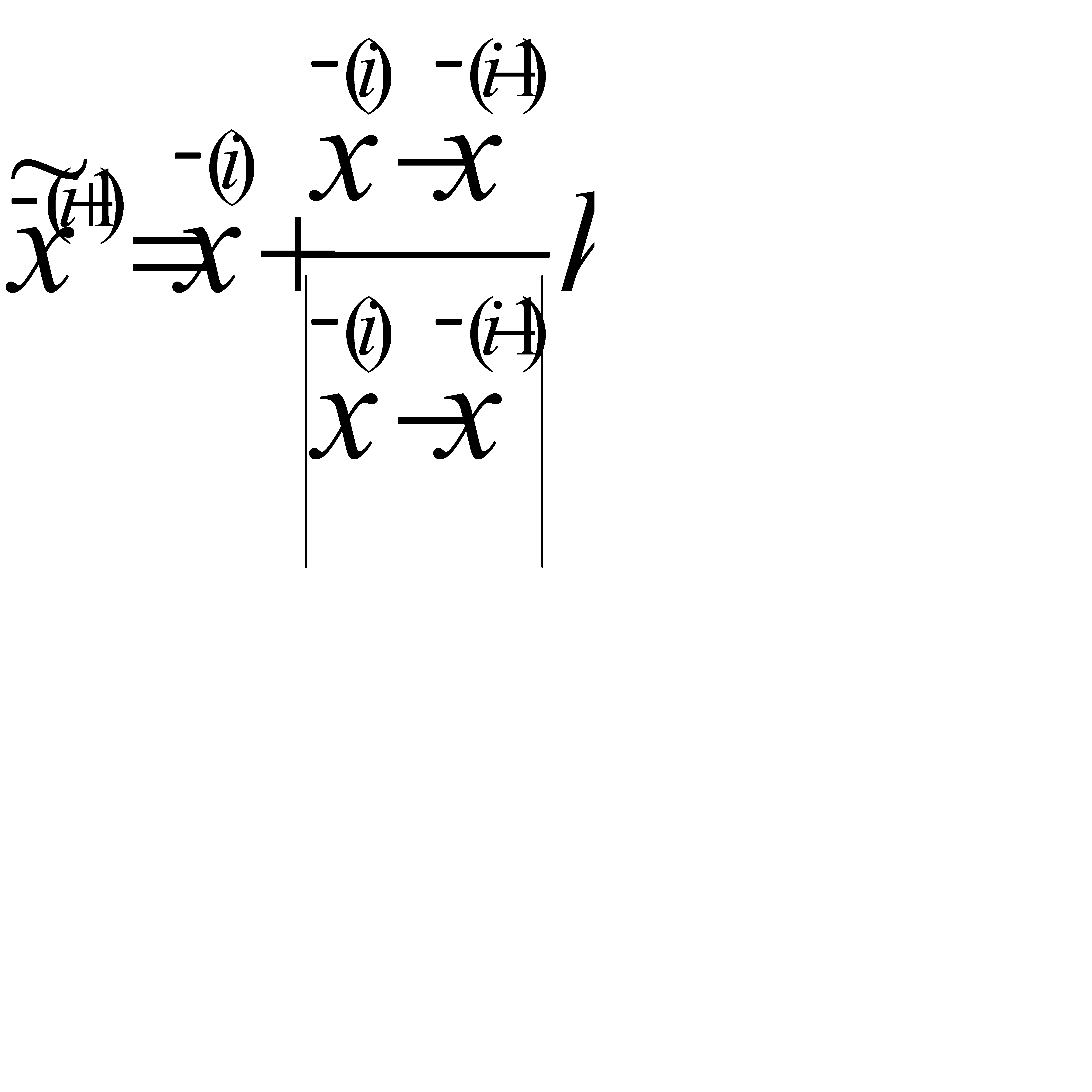(2.57)

Особую роль в процедуре «овражного» поиска играет выбор длины «овражного» шага h. Большой шаг может затруднить поиск, т.к. не позволяет следить за изгибами «дна оврага», с малым шагом связаны значительные затраты машинного времени. Величина h выбирается значительно больше величины спускового шага. Кроме того, при выборе длины шага, также как и при выборе направления движения к оптимуму может осуществляться адаптация в процессе поиска.

2.6 Глобальный поиск оптимума

Поиск оптимальных параметров проектируемого объекта, как правило, осуществляется в условиях отсутствия информации о числе локальных экстремумов критерия оптимальности, сложности геометрии допустимой области и т.д. Поэтому задача оптимального проектирования является много- экстремальной задачей, заключающейся в определении глобального оптимума по информации о математической модели проектируемого объекта, накапливаемой в процессе поиска.

Основная трудность разработки алгоритмов поиска глобального оптимума заключается в том, что с помощью ЭВМ не удается собрать информацию о характере изменения функции во всей допустимой области. Практически все рассмотренные способы поиска локального экстремума не могут быть использованы без специальных модификаций для поиска глобального экстремума. Исключение составляет метод полного перебора, однако использование его на практике неудобно из-за слишком больших затрат машинного времени на поиск. Как правило, методы поиска глобального экстремума базируются на применении методов случайного поиска. Это объясняется тем, что поиск случайными методами позволяет управлять плотностью распределения независимых пробных шагов, сосредотачивать поисковые шаги в местах наиболее вероятного нахождения глобального оптимума и др.

Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов

Алгоритм описывается следующей рекуррентной формулой [46]

(2.58)

(2.59)

где - это i -ое пробное состояние, выбранное случайно и сохраняемое в памяти в случае удачной пробы;

- вычисленное в i -ом пробном состоянии значение функции качества и сохраняемое в памяти в случае удачной пробы.

При равномерной плотности распределения пробных шагов поиск разделяется на k этапов из пробных шагов j=1, 2, …k.

Каждый пробный шаг осуществляется внутри гиперпараллелепипеда пространства независимых переменных , т.е.

(2.60)

причём стороны гиперпараллелепипеда с каждым j- ым этапом уменьшаются в c>1 по сравнению с (j- 1) этапом в соответствии с формулой

(2.61)

(2.62)

где - точка, соответствующая пробному шагу с наименьшим значением функции качества из всех проб на (j -1) этапе.

Несмотря на равномерную плотность распределения пробных шагов внутри каждого этапа, происходит увеличение плотности распределения от этапа к этому за счёт уменьшения зоны поиска, т.е.

(2.63)

где - плотность распределения пробных шагов на j -ом этапе;

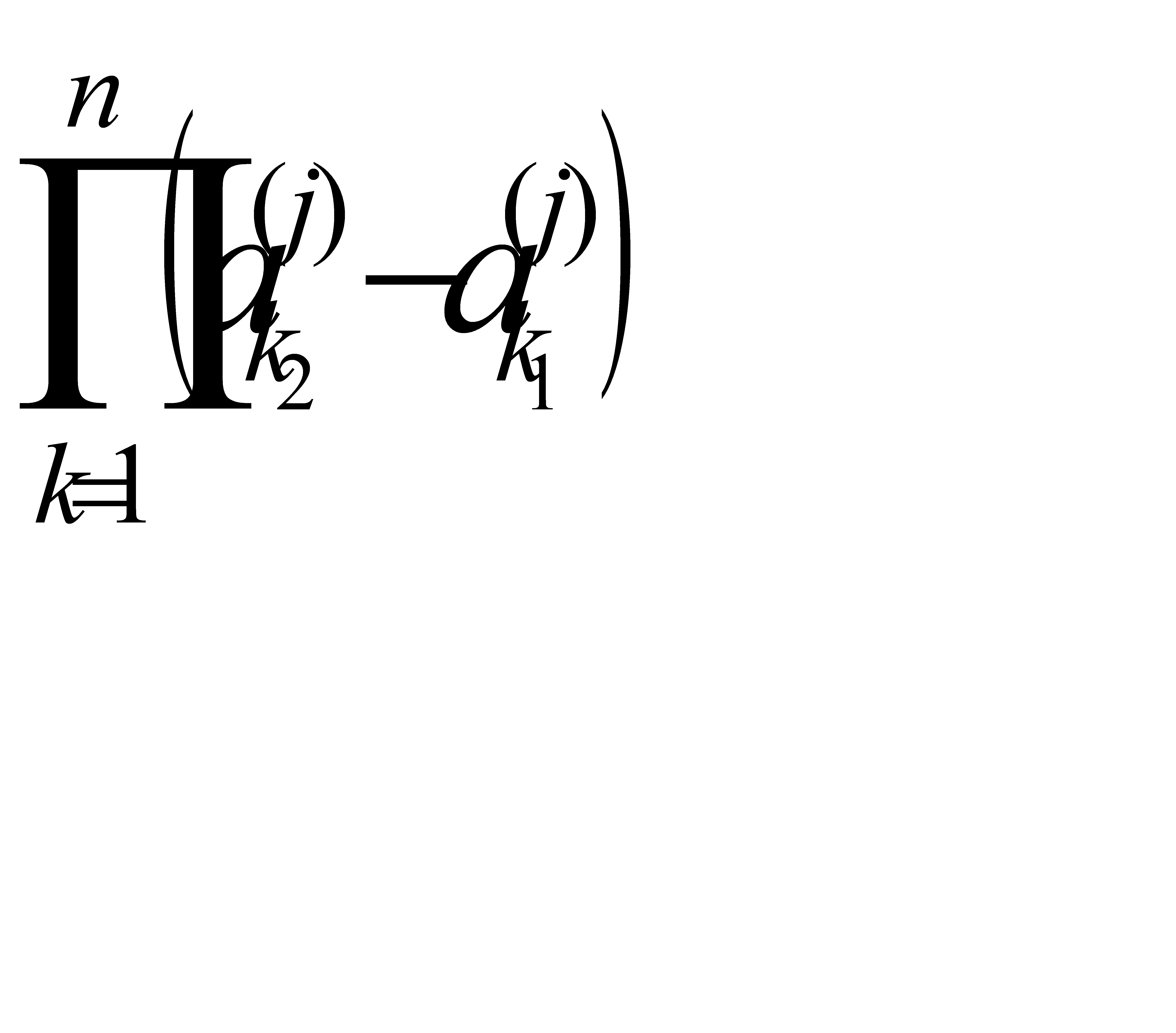- объём гиперпараллелепипеда на j -ом этапе.

Иногда целесообразно пробные шаги на каждом последующем этапе распределять не равномерно, а по нормальному закону

, (2.64)

где

- исходная дисперсия; 0< q <1.

Итак, случайные пробные шаги нормально распределены со средним значением, совпадающим с наилучшей величиной критерия качества из всех проб этапа, а дисперсия уменьшается при неудачных шагах и увеличивается до исходного значения при удачных шагах.

Локально-глобальный поиск коллективом автоматов Буша – Мостселлера

Рассмотрим алгоритм [47] нахождения в области D, осуществляющий шаговый поиск, где шаг , а выбор знаков приращения производится адаптивным алгоритмом.

Алгоритм может работать в двух режимах – глобальном и локальном, причём при переходе на локальный режим надо поменять местами параметры адаптации α и β (см. ниже).

1) Обучение. Обозначая через вероятность выбора положительного направления по i -ой координате на N -ом шаге поиска получим:

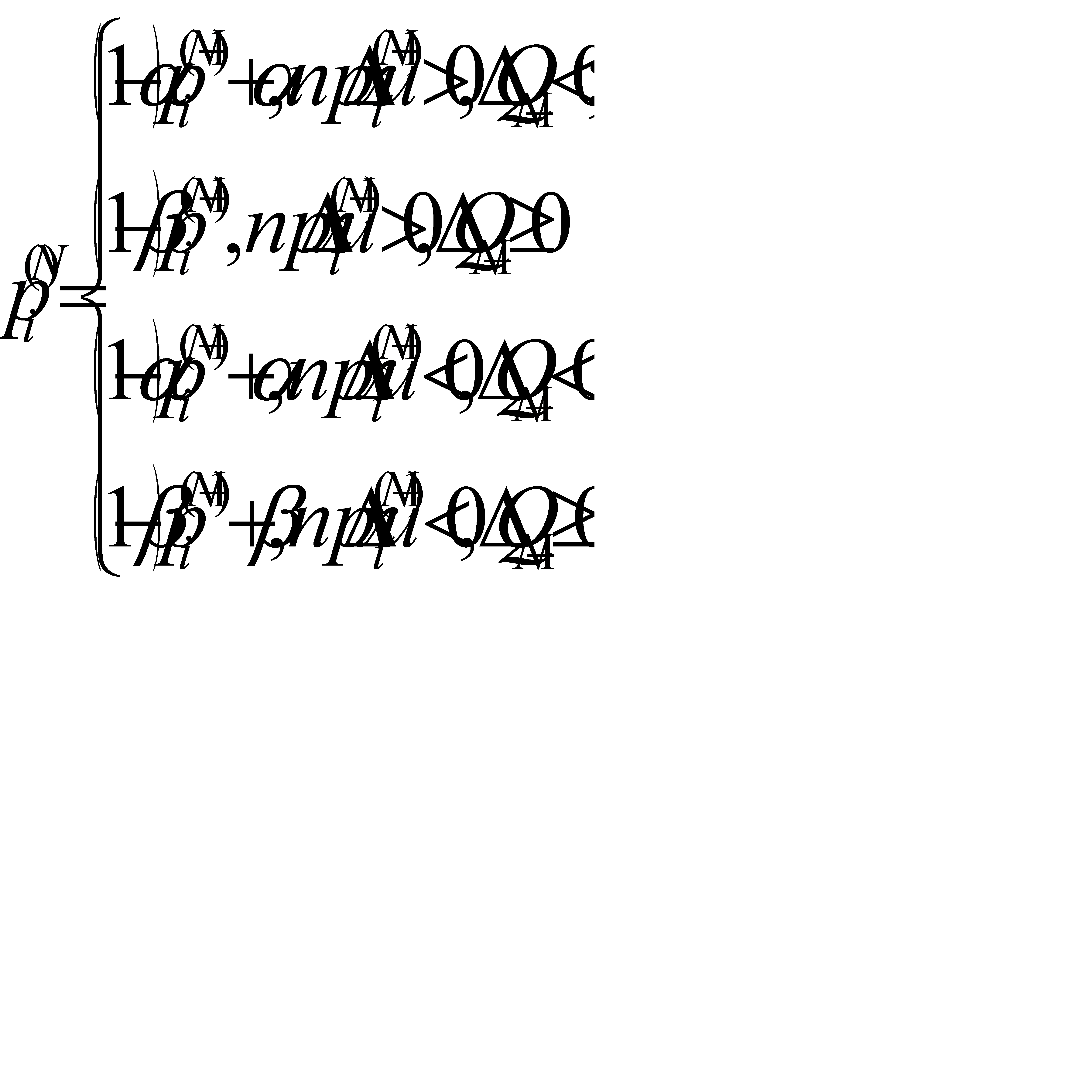(2.65)

2) Роль соотношения между α и β. При α > β поиск имеет глобальный характер. Это связано с тем, что скорость разгона при движении вниз больше, чем скорость торможения при подъёме. При α < β происходит локальный поиск, т.к. торможение преобладает над разгоном. Движение напоминает затухающие колебания. При α = β алгоритм недостаточно эффективен. Происходит блуждание в некоторой, довольно широкой окрестности минимума без уменьшения размеров этой окрестности.

3) Поиск вблизи границы области. Если очередной шаг выводит за границы области, то этот шаг не производится, но адаптация происходит. Для адаптации применяется один из следующих способов:

4) вероятности обрабатываются по формулам (2.65),

5) соответствующим торможению ;

производится отражение, т.е. (2.66)

Для локального поиска оба способа хороши. Для глобального поиска способ 2 предпочтителен, т.к. при способе 1 затруднен выход из области притяжения локального минимума, хотя сам этот минимум может быть найден быстрее.

6) Использование ∆ Q при обратной связи. После каждого очередного шага обучение проводится по формулам (2.65), однако с переменными α и β. Задаются (максимальные α и β), а также параметр забывания . После очередного шага вычисляется при помощи следующих формул (для формулы аналогичны):

(2.67)

Применение изложенной процедуры делает адаптацию значительно более гибкой. При и становятся постоянными.

Исходными данными для алгоритма является: n – размерность пространства независимых переменных; – количество шагов глобального исследования; k – количество точек, подлежащих локальному уточнению; - параметры адаптации (); - коэффициент забывания; - коэффициент уменьшения шагов; - параметр остановки; и - соответственно начальная точка и начальные шаги.

Алгоритм состоит из следующих этапов:

1) на первых шагах происходит, глобальный поиск из данной начальной точки с шагами и вероятностями, равными 0,5;

2) в процессе глобального поиска происходит адаптация по формулам (2.65) с переменными, определяемыми по формулам (2.67). На границе применяется отражение (2.66);

3) результат глобального поиска состоит в определении k наилучших точек;

4) после окончания работы глобальной части производится k локальных поисков из точек полученного набора с прежними начальными шагами и начальными вероятностями, равными 0,5;

5) в процессе каждого локального поиска производится адаптация: на границе – по формулам (2.66), внутри области - по формулам (2.65) с постоянным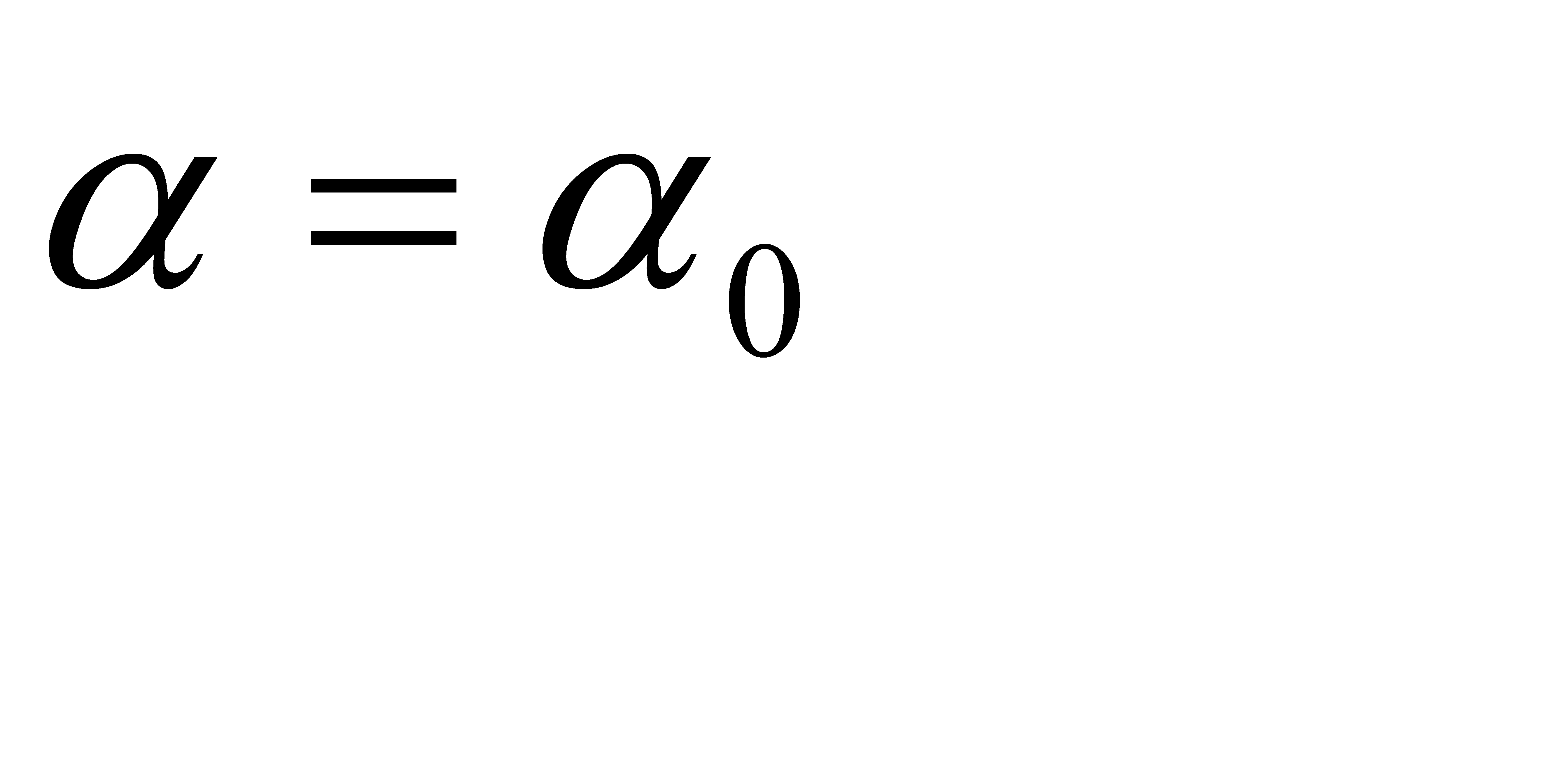и и .

6) если при двух последующих двойных подсчётах функции качества знаки приращений некоторой переменной были + +, – –, или – –, + +, то шаг по этой переменной умножается на j;

7) каждый локальный поиск заканчивается, когда шаги по всем переменным станут меньше ;

8) при минимизации тестовой функции использованы следующие параметры алгоритма [47] . На три локальных поиска было затрачено 770 шагов.

2.7 Сравнительный анализ методов оптимизации

Разнообразие и сложность реальных задач принятия оптимальных решений требуют создания эффективных надёжных средств поиска оптимизма. В настоящее время для решения оптимизационных задач одного и того же класса разработано большое число поисковых алгоритмов [1, 3-8, 24,25, 42,48-61]. Это приводит к тому, что у исследователя перед решением конкретной задачи возникают вопросы о выборе метода оптимизации, являющегося в каком – то смысле наилучшим. При этом обычно ориентируются на принадлежность объекта оптимизации к тому или иному классу, способ задания критерия оптимальности, сложность реализации модели объекта на ЭВМ, математические особенности критерия оптимальности и др. Выбор метода зависит также от личных склонностей и уровня подготовки следователя. Анализ перечисленных факторов показывает, что выбор метода оптимизации является весьма субъективным. Это обстоятельство в какой – то степени затрудняет возможность выработки единых рекомендаций по выбору метода оптимизации. Однако основанные на опыте частные рекомендации в значительной мере могут облегчить работу исследователя при решении конкретных задач оптимизации. Поэтому целью настоящего раздела является систематизация и обобщение работ в этом направлении для решения актуальной проблемы выбора эффективных методов решения оптимизационных задач. Сравнительный анализ работоспособности и эффективности алгоритмов оптимизации, проведенный как в нашей стране [1, 4, 8, 20, 52-57], так и за рубежом [3, 4, 24, 42, 58-61], не позволяет априори утверждать, что один метод заведомо лучше другого. Это не случайно – каждый метод оптимален для определенного класса функций, причём выявить точное соответствие между функциями и методами оптимизации в настоящее время не представляется возможным. По этой причине приводимые в литературе [7, 8, 25, 42,51] рекомендации по выбору методов оптимизации являются ориентировочными. Тем не менее общая тенденция не вызывает сомнений: наиболее эффективными являются методы первого и второго порядков, а наименее эффективными – методы нулевого порядка [8].

Таким образом, однозначного ответа на вопрос о выборе метода оптимизации получить нельзя и при решении оптимизационных задач можно воспользоваться рекомендациями [8, 42]:

1) если оптимизируемая функция не дифференцируема, то используют методы нулевого порядка;

2) если оптимизируемая функция дифференцируема, но аналитические выражения её производных неизвестны, то используют градиентные методы, основывающиеся на замене аналитического дифференцирования численным – квазиградиентные методы;

3) при поиске глобального экстремума повторяют несколько раз процедуру оптимизации в соответствии с правилами 1) и 2) из начальных точек, выбираемых случайным образом в допустимой области изменения оптимизируемых параметров;

4) если оптимизируемая функция овражного типа и не имеет седловых точек, то используют методы переменной метрики [2, 4];

5) если оптимизируемая функция имеет седловую точку, то используют методы нулевого порядка (Нелдера – Мида или Пауэлла), либо переходят к п.6;

6) если вид оптимизируемой функции не известен, то используют комбинации методов:

6.1) методы переменной метрики;

6.2) метод Нелдера – Мида (либо метод Пауэлла). Если его работа успешна, то через несколько шагов следует вернуться к методам п. 6.1.

Авторы [1] считают: не поиск универсального метода, а разумное сочетание разнообразных методов позволяет с наибольше эффективностью решать оптимизационные задачи.

В порядке обсуждения вышеуказанных рекомендаций следует отметить, что правила 1), 2) обусловлены теоретическими исследованиями и подтверждены практическими расчётами [3, 4, 8]. Некоторыми из наиболее эффективных и надёжных методов являются [3-5, 8, 25]:

1) среди методов первого порядка – методы переменной метрики и Флетчера – Ривса;

2) среди методов нулевого порядка симплексный метод Нелдера – Мида и метод покоординатного спуска Пауэлла.

Приведённые в [8] результаты тестовых расчётов демонстрируют преимущества отмеченных методов. Работа [8] содержит подробные обсуждения рекомендаций относительно выбора методов в различных поисковых ситуациях (окрестность экстремума, седловая точка, овраги).

Необходимо отметить, что не в меньшей степени на выбор метода оптимизации влияет и наличие программной реализации соответствующего алгоритма. При использовании программ, рассчитанных на решение некоторого класса задач различными методами (в соответствии с рекомендациями п. 6), важными представляются вопросы стандартизации обращения к этим программам. Стандартное обращение позволяет легко заменить при необходимости одну программу на другую, использовать имена программ в качестве параметров при разработке другой программы и т.д.

Не нашли, что искали? Воспользуйтесь поиском: