
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Выбор независимых переменных 10 страница
 - активное сопротивление обмотки возбуждения;
- активное сопротивление обмотки возбуждения;
 - индуктивность реакции статора по продольной оси;
- индуктивность реакции статора по продольной оси;
 - индуктивность статорной обмотки по поперечной оси.
- индуктивность статорной обмотки по поперечной оси.
Интервал изменения оптимизируемых параметров составляет  от номинальных значений.
от номинальных значений.
Для оптимизации используются следующие методы НЛП:
1) метод случайного поиска с адаптацией шага [34];
2) метод Келли - Уиллинга, содержащий элементы адаптации и самообучения [4];
3) метод наискорейшего спуска [41].
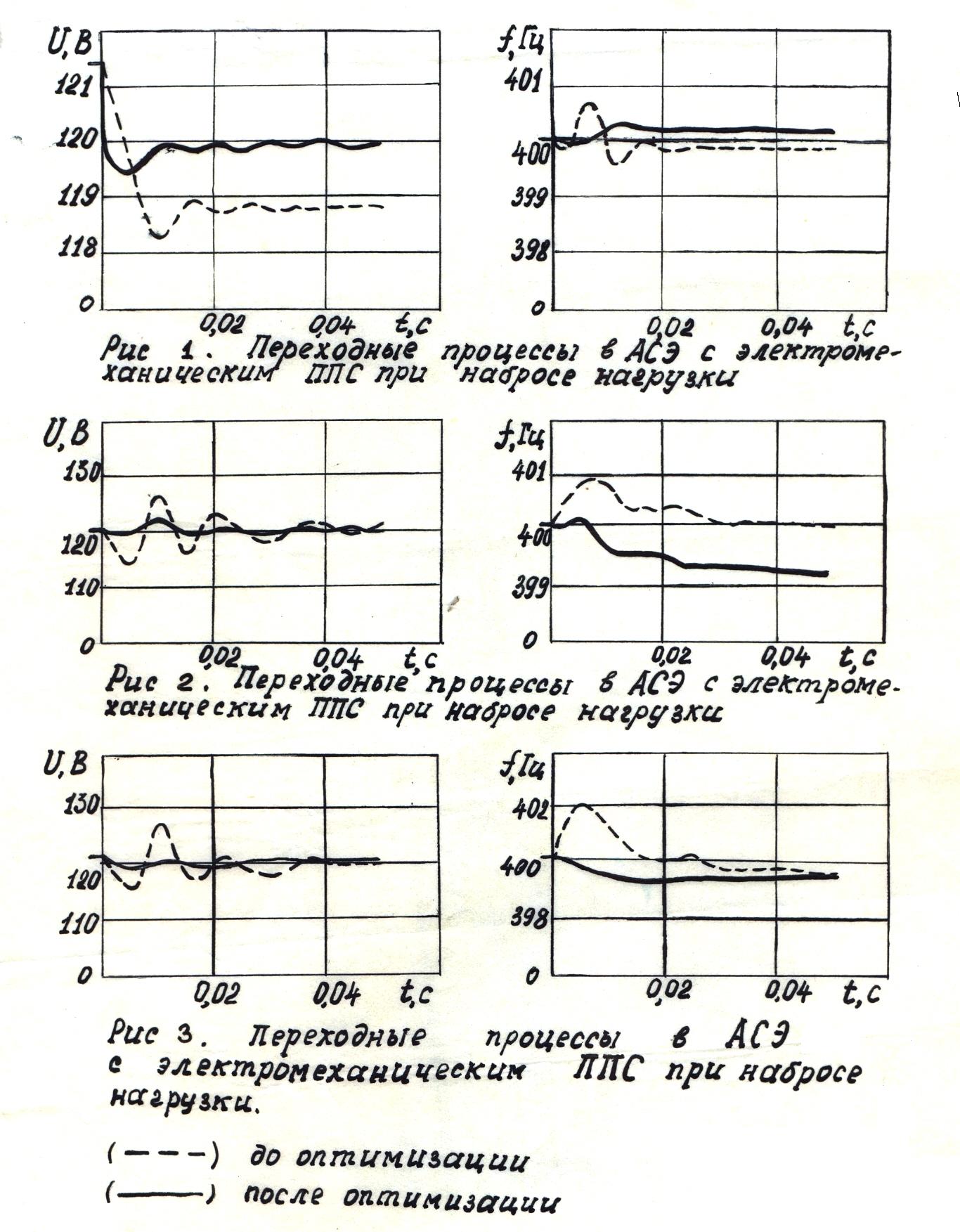
В таблице 5.17 приведены результаты поиска минимума критерия оптимальности методом [34]: за 100 шагов удалось на порядок снизить показатель качества  . Переходные процессы режима наброса номинальной нагрузки до оптимизации (штриховые линии) и после оптимизации (сплошные линии) приведены на рис. 5.4.
. Переходные процессы режима наброса номинальной нагрузки до оптимизации (штриховые линии) и после оптимизации (сплошные линии) приведены на рис. 5.4.
Исследование проводилось при оптимальных регуляторах напряжения и частоты [13].
Регуляторы представлены в математическом описании АСЭ уравнениями

Где  ,
,  - уставки регуляторов,
- уставки регуляторов,
 - отклонение тока в линии постоянного тока [10].
- отклонение тока в линии постоянного тока [10].
Как видно из сравнения кривых, путём изменения параметров СГ удалось добиться снижения колебательности процесса по координатам U, f. Некоторые параметры СГ в результате оптимизации достигли нижних границ области ( ).
).
Далее были проведены расчёты с использованием метода Келли-Уиллинга [4].
Результаты поиска представлены в таблице 5.18, переходные процессы на рис. 5.5. За 148 шагов поиска значение критерия качества уменьшилось почти в 3 раза. Причина отклонения частоты от уровня 400 Гц после оптимизации (рис. 5.5) связана со значениями весовых коэффициентов ( ). За счёт увеличения
). За счёт увеличения  можно было добиться улучшения качества процесса по частоте.
можно было добиться улучшения качества процесса по частоте.
В следующей серии вычислительных экспериментов оптимизация была осуществлена с использованием детерминированного метода НЛП - метода наискорейшего спуска [41]. Как и ранее, исследование проводилось для режима включения статической нагрузки при оптимальных регуляторах напряжения и частоты. При этом постоянная времени обмотки возбуждения была постоянной.
В качестве оптимизируемых параметров СГ были выбраны  ,
,  ,
, 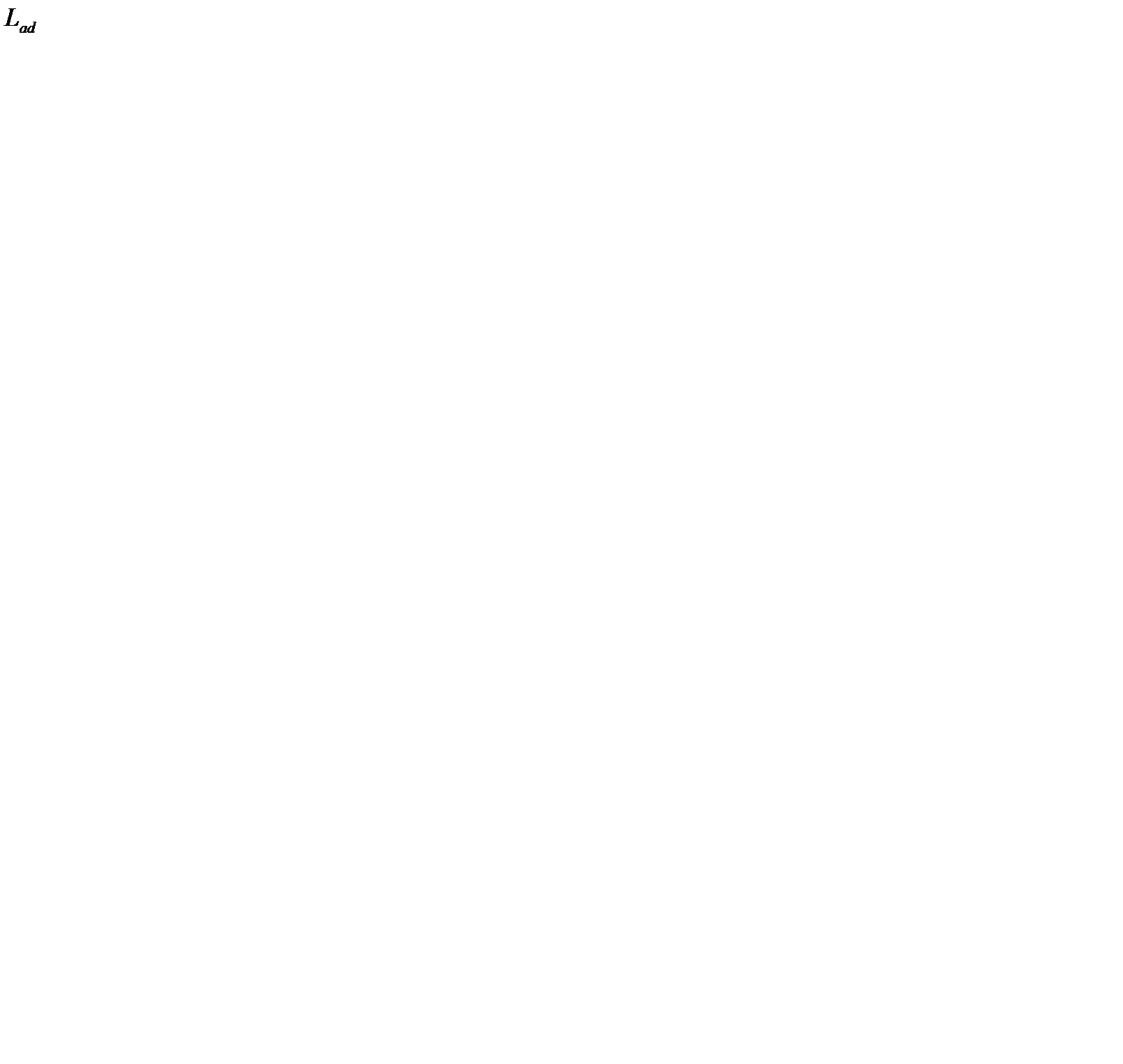 ,
,  ,
,  ,
,
Результаты поиска приведены в таблице 5.19, кривые переходных процессов - на рис. 5.6.
Результаты проведённых исследований свидетельствуют о том, что для улучшения качества переходных процессов в АСЭ при варьировании параметров объекта регулирования необходимо уменьшать параметры СГ (причём, такие как  ,
,  в большей степени, чем
в большей степени, чем 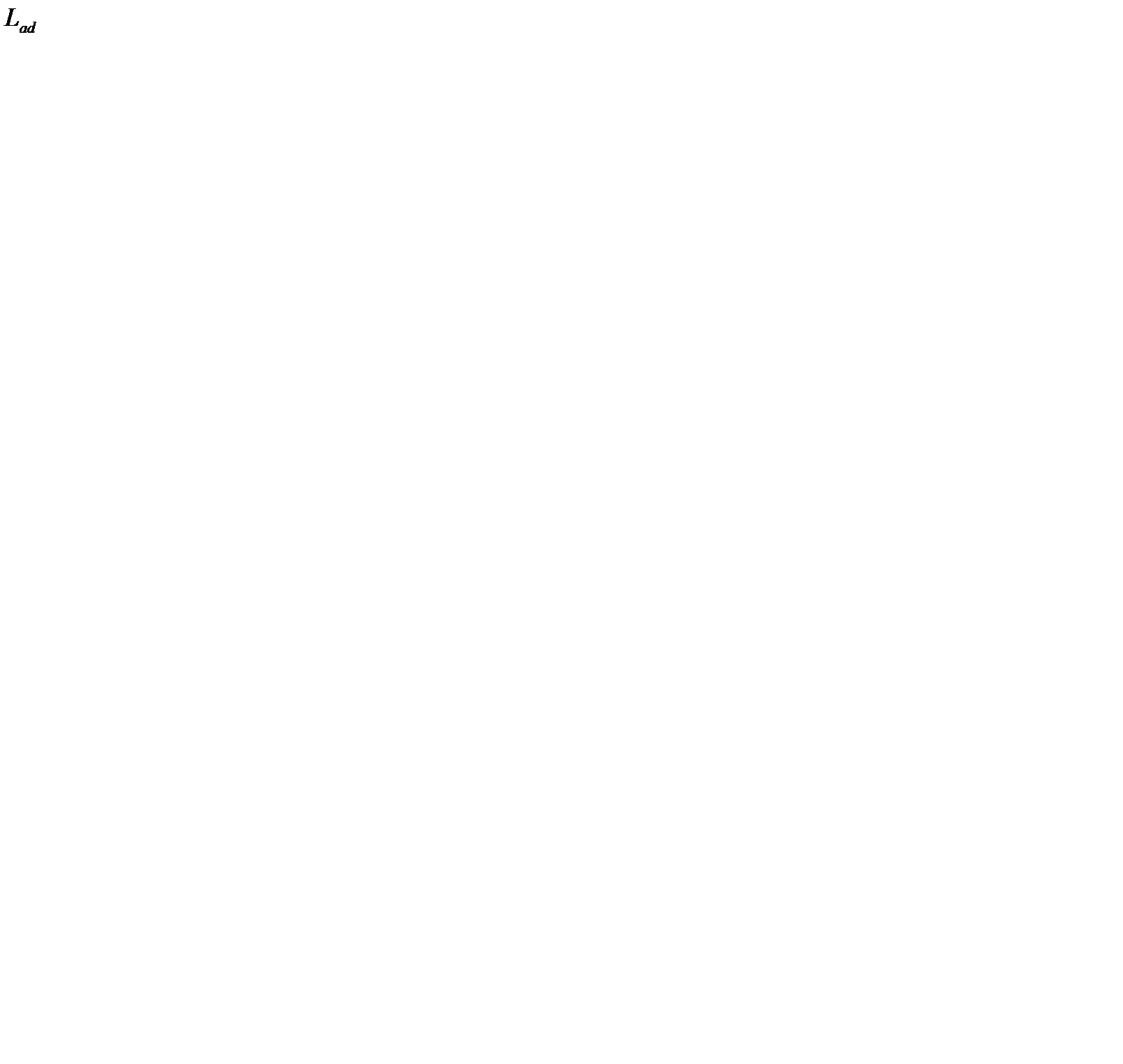 ,
,  ).
).
Сравнительный анализ численных методов оптимизации демонстрирует достоинство метода наискорейшего спуска, заключающееся в значительном снижении функции качества за приемлемое количество шагов.
В целом результаты проделанной работы свидетельствуют о перспективности применения методов нелинейного программирования для оптимального проектирования электрических машин автономных электроэнергетических систем.
Результаты оптимизации параметров СГ из условий minQ в режиме наброса нагрузки  (оптимальный регулятор)
(оптимальный регулятор)
| Переходные процессы в АСЭ с электромеханическим ППС при набросе нагрузки |
| Рис. 5.6 |
| Переходные процессы в АСЭ с электромеханическим ППС при набросе нагрузки |
| Рис. 5.4 |
| Переходные процессы в АСЭ с электромеханическим ППС при набросе нагрузки |
| Рис. 5.5 |
| (─ ─ ─) до оптимизации () после отимизации |
Оптимизация параметров СГ в АСЭ с эл. мех. ППС при набросе нагрузки
(метод случайного поиска)
Таблица 5.17
| Число шагов N | Показатель качества Q | 
| 
| 
| 
| 
| 
| |

| 
| 
| 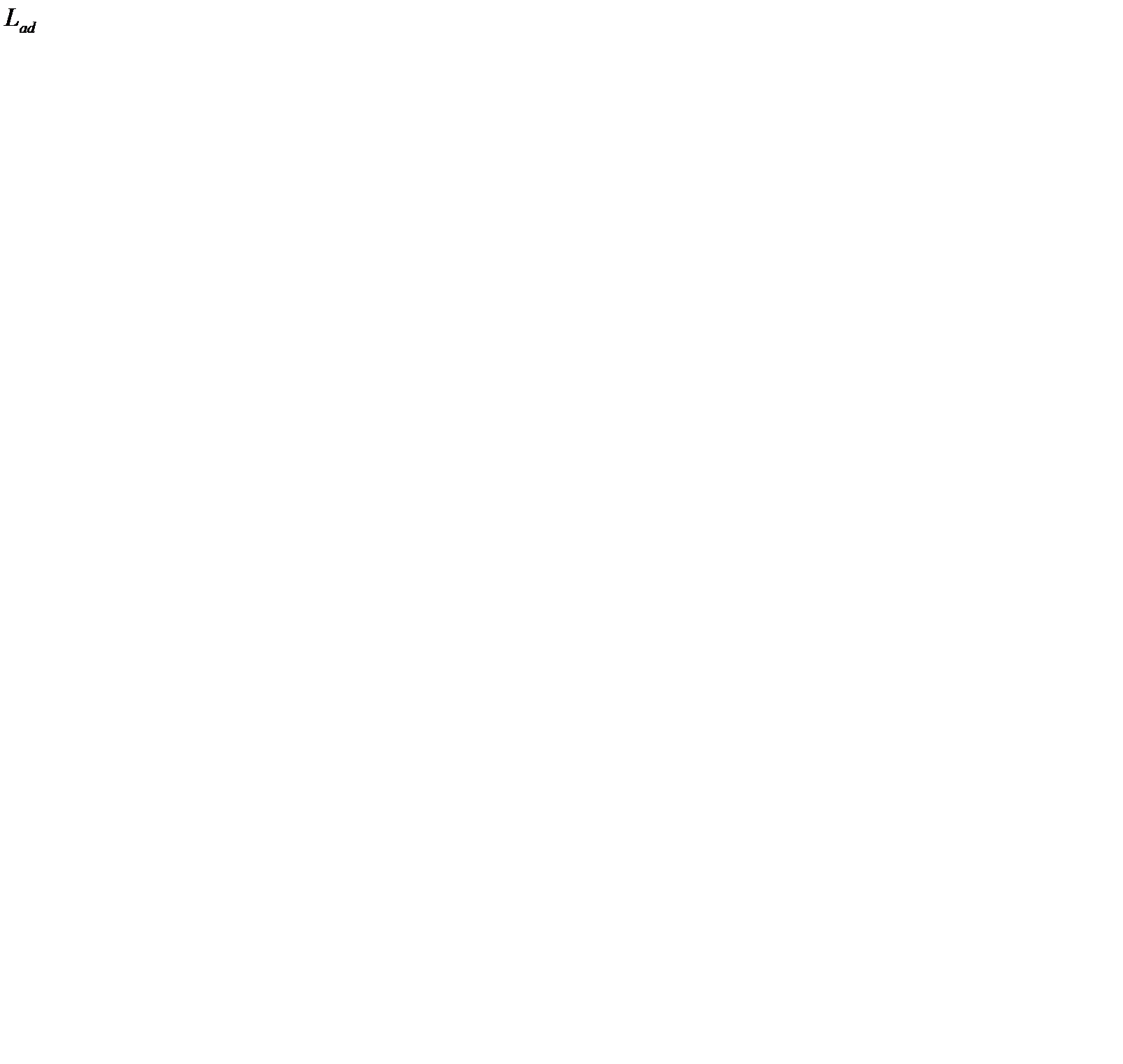
| 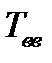
| 
| |||
| 0.168 | 
| 
| 
| 
| 
| 2.36 | ||

| 
| 
| 
| 
| 
| 2.36 | ||

| 
| 
| 
| 
| 
| 2.29 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||

| 
| 
| 
| 
| 
| 2.13 | ||
| Ограничения на параметры СГ | Верхние | 
| 
| 
| 
| 
| 2.95 | |
| Нижние | 
| 
| 
| 
| 
| 1.77 | ||
Таблица 5.18
Оптимизация параметров СГ в АСЭ с эл.мех. ППС
при набросе нагрузки (метод Келли-Уиллинга)
| Число удач. шагов Nуд | Общее число шагов N | Функ ция качества Q | 
| 
| 
| 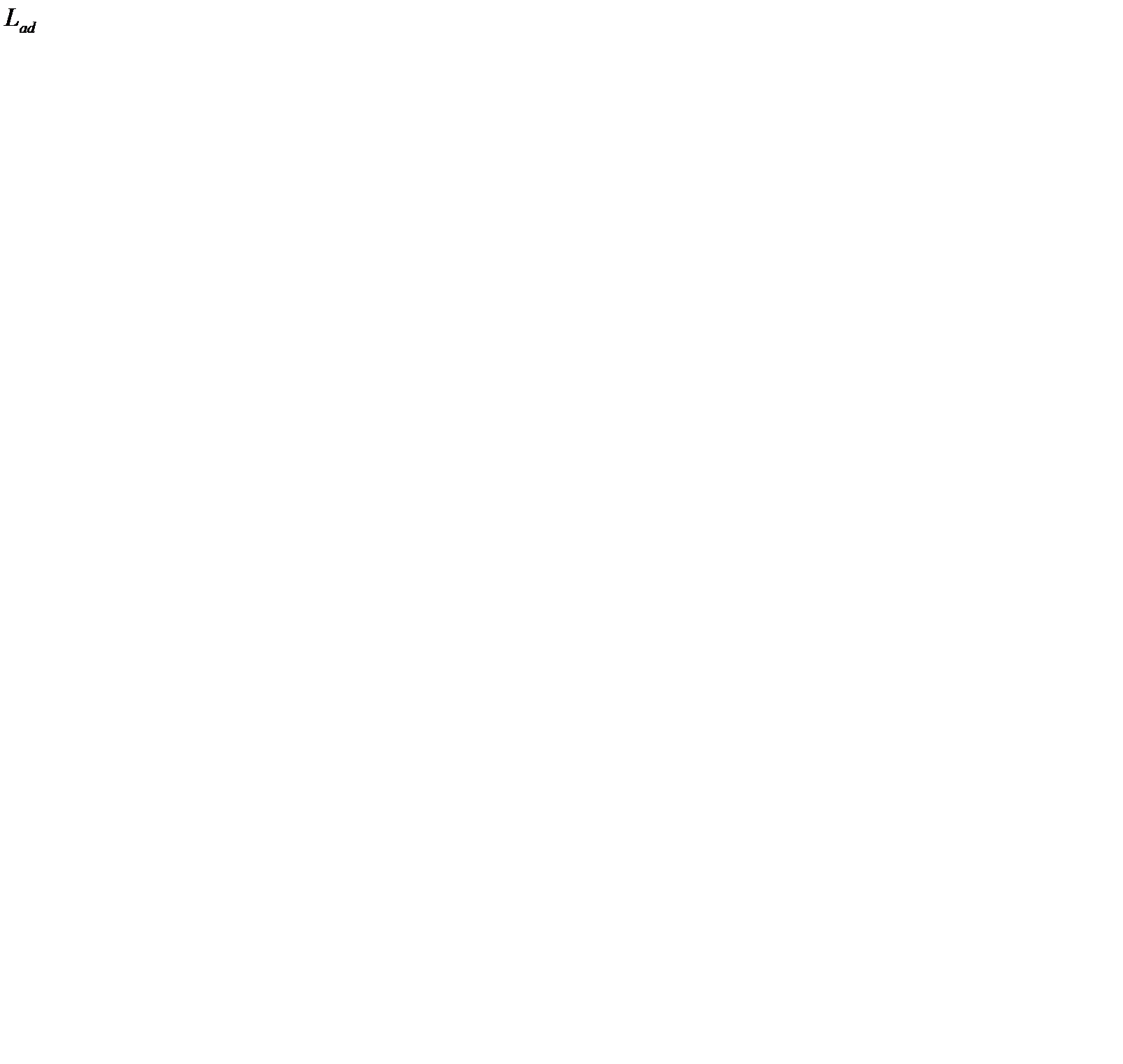
| 
| 
|

| 
| 
| 
| 
| 
| |||
| Ом | Ом | Гн | Гн | - | Ом | |||
| 0,5090 | 0,1998 | 0,3024 | 0,2729 | 0,5189 | 0,5448 | 0,2354 | ||
| 0,4885 | 0,2 | 0,307 | 0,268 | 0,521 | 0,55 | 0,1834 | ||
| 0,4576 | 0,1996 | 0,302 | 0,264 | 0,529 | 0,554 | 0,1856 | ||
| 0,4391 | 0,2 | 0,306 | 0,258 | 0,54 | 0,567 | 0,183 | ||
| 0,406 | 0,201 | 0,303 | 0,253 | 0,547 | 0,567 | 0,188 | ||
| 0,4045 | 0,202 | 0,3065 | 0,251 | 0,546 | 0,574 | 0,189 | ||
| 0,39 | 0,198 | 0,309 | 0,253 | 0,543 | 0,571 | 0,193 | ||
| 0,37 | 0,195 | 0,31 | 0,25 | 0,54 | 0,575 | 0,196 | ||
| 0,36 | 0,193 | 0,309 | 0,248 | 0,546 | 0,576 | 0,197 | ||
| 0,31 | 0,1988 | 0,263 | 0,227 | 0,544 | 0,477 | 0,177 | ||
| 0,3 | 0,1989 | 0,268 | 0,231 | 0,554 | 0,46 | 0,186 | ||
| 0,25 | 0,194 | 0,236 | 0,23 | 0,53 | 0,424 | 0,19 | ||
| 0,215 | 0,198 | 0,225 | 0,206 | 0,527 | 0,425 | 0,184 | ||
| 0,187 | 0,185 | 0,225 | 0,206 | 0,549 | 0,4 | 0,191 | ||
| 0,186 | 0,177 | 0,225 | 0,215 | 0,54 | 0,4 | 0,202 | ||
| 0,164 | 0,156 | 0,254 | 0,207 | 0,98 | 0,4 | 0,193 | ||
| Область поиска | Верхний уровень | 0,2488 | 0,375 | 0,344 | 0,6525 | 0,68 | 0,295 | |
| Нижний уровень | 0,1493 | 0,225 | 0,206 | 0,39 | 0,4 | 0,177 |
Таблица 5.19
Оптимизация параметров СГ в АСЭ с эл.мех. ППС при набросе нагрузки (метод наискорейшего спуска)

| 
| 
| 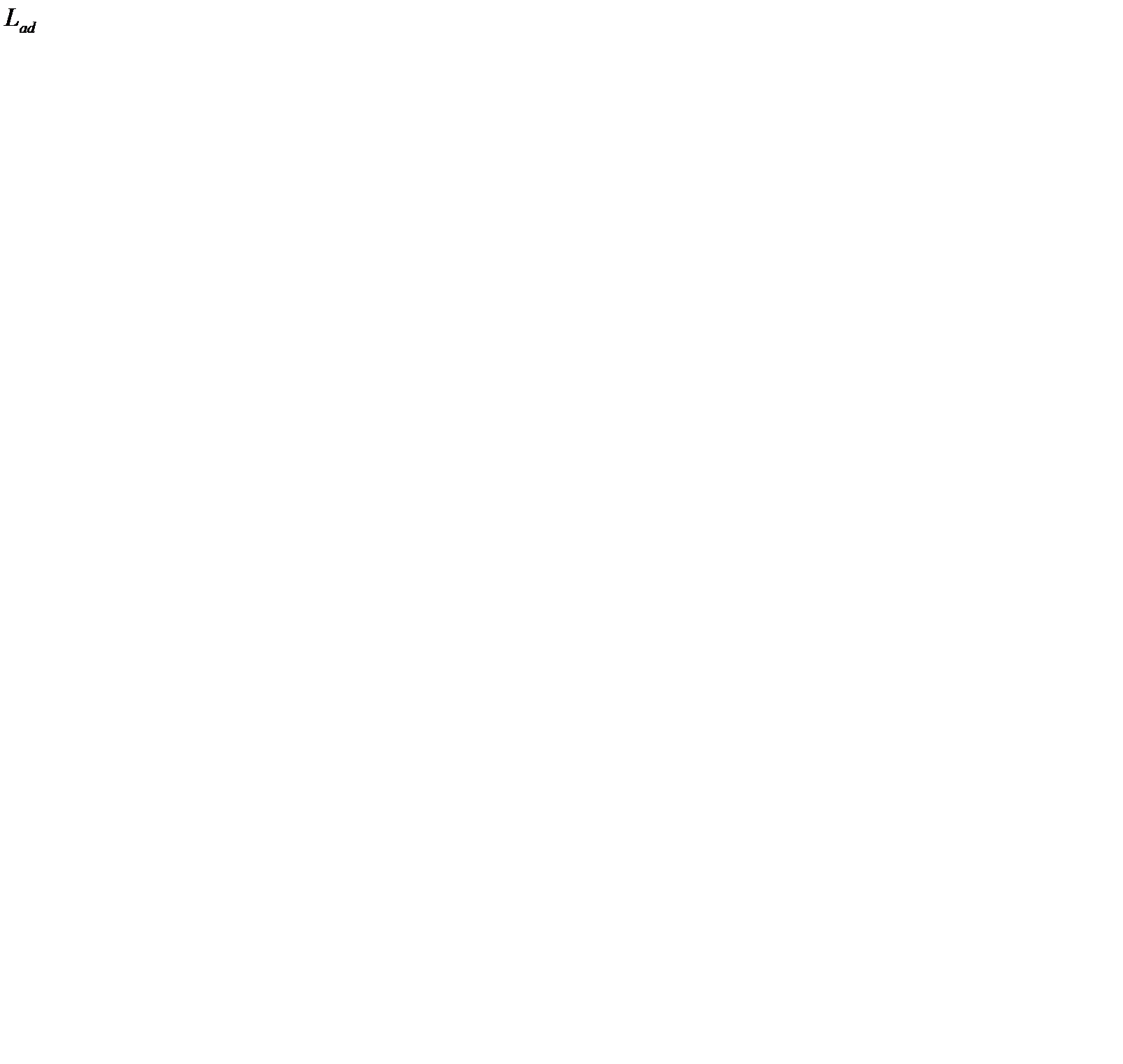
| 
| 
| ||

| 
| 
| 
| 
| 
| ||
| N | Q | 
| 
| 
| 
| 
| 
|
| 0,516002 | 0,199 | 0,3 | 0,275 | 0,522 | 0,54 | 0,236 | |
| 0,516 | 0,15 | 0,225 | 0,205 | 0,653 | 0,4 | 0,177 | |
| 0,2043 | 0,15 | 0,225 | 0,205 | 0,653 | 0,4 | 0,177 | |
| 0,2043 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,2272 | |
| 0,23393 | 0,15 | 0,225 | 0,205 | 0,653 | 0,4 | 0,177 | |
| 0,2043 | 0,15 | 0,225 | 0,205 | 0,653 | 0,4 | 0,177 | |
| 0,2043 | 0,15 | 0,225 | 0,205 | 0,4943 | 0,4 | 0,1806 | |
| 0,15776 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,1842 | |
| 0,13801 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,1878 | |
| 0,13909 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,1873 | |
| 0,13888 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,1868 | |
| 0,13808 | 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,1842 | |

| 0,25 | 0,375 | 0,345 | 0,653 | 0,68 | 0,295 | |

| 0,15 | 0,225 | 0,205 | 0,3925 | 0,4 | 0,177 |
5.2.3 Оптимизация динамических свойств САУ.
Рассмотрим еще один пример применения методов полинейного программирования для оптимизации динамических свойств системы автоматического управления (САУ) [90].
Техническое задание на проектирование САУ обычно содержит ряд требований, предъявляемых к различным её характеристикам, в том числе, к показателям качества переходных процессов, динамической ошибке и т.п.
Задача получения требуемого качества переходного процесса в САУ формируется как задача параметрической оптимизации, т.е. при заданном описании объекта определить некоторые параметры  САУ, обеспечивающие минимум интегральной оценки
САУ, обеспечивающие минимум интегральной оценки
 ,
, 
где  - интервал времени интегрирования;
- интервал времени интегрирования;
 ) - результат моделирования динамики САУ;
) - результат моделирования динамики САУ;
 - заданная функция времени.
- заданная функция времени.
Объект управления (нелинейная следящая система [91, задача 409], структурная схема которой изображена на рис. 5.7 имеет следующие значения параметров:
 Статическая характеристика
Статическая характеристика  нелинейного звена показана на рис. 5.8, где b=0.5, c=1.5. Переходный процесс в системе рассчитывался при ступенчатом задающем воздействии
нелинейного звена показана на рис. 5.8, где b=0.5, c=1.5. Переходный процесс в системе рассчитывался при ступенчатом задающем воздействии  . В качестве
. В качестве 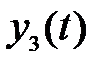 берётся изменение
берётся изменение  . Моделирование динамики системы осуществляется с использованием стандартной программы, реализующей метод Хемминга [92]. Начальные условия для переменных системы дифференциальных уравнений – нулевые. Интегрирование ведётся в интервале
. Моделирование динамики системы осуществляется с использованием стандартной программы, реализующей метод Хемминга [92]. Начальные условия для переменных системы дифференциальных уравнений – нулевые. Интегрирование ведётся в интервале  с шагом 0.0025 с.
с шагом 0.0025 с.
Оптимизация осуществляется ведется по четырем параметрам САУ: 
Результаты оптимизации различными алгоритмами НЛП сведены в таблицу 5.19. Переходные процессы в САУ с исходными параметрами и с параметрами, полученными в результате оптимизации по критерию минимума интегральной оценки, приведены на рис. 5.9. Видно, что сравнительно хорошие результаты дало применение градиентного метода, при этом постоянные времени  достигли нижних границ области поиска.
достигли нижних границ области поиска.

|

|

|

|

|
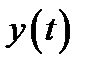
|

|
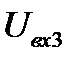
|

|

|

|

|

|
|
Не нашли, что искали? Воспользуйтесь поиском: