
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Выбор независимых переменных 7 страница
N – число независимых переменных целевой функции, 1  N
N  50;
50;
X(150) – массив из 3*N чисел: в первых N элементах записаны координаты начальной точки  ; следующие N элементов – верхние ограничения на независимые переменные; последние N элементов – нижние ограничения на независимые переменные вида
; следующие N элементов – верхние ограничения на независимые переменные; последние N элементов – нижние ограничения на независимые переменные вида
 .
.
Входными данными, управляющими ходом каждой из процедур оптимизации являются:
JCN – общее число шагов поиска, задаваемое пользователем;
JCP – организатор вывода информации на печать;
DX – длина шага поиска  ;
;
DXMIN – минимальный шаг поиска;
G1, G2 – коэффициенты соответственно увеличения и уменьшения шага поиска;
K1 - ограничитель числа «неудачных» шагов поиска («неудачным» называется шаг, когда  при поиске
при поиске  ). При достижении счётчика «неудачных» шагов значения K1, шаг поиска уменьшается в R8 раз;
). При достижении счётчика «неудачных» шагов значения K1, шаг поиска уменьшается в R8 раз;
DEX(50) – масштабные коэффициенты, определяемые как [X(I+N) – X(I+2*N)]/2. Размерность массива N.
EPSD, EPSQ – величины относительных погрешностей, служащие критерием останова.
Перечисленные параметры, а также параметры алгоритмов оптимизации формируются в подпрограмме BLOCK DATA. Не исключается возможность ввода вышеуказанных параметров с клавиатуры. Выходными данными для всех программ оптимизации являются:
JC6 – текущее значение числа вычислений функций качества;
JC2, JC4 – соответственно число «удачных» и «неудачных» шагов поиска;
QN – значение функции качества, минимальное за JC6 шагов поиска;
XT(I) – массив текущих значений аргументов (координаты точки, в которой достигается минимум, исходная точка для следующей итерации);
DX – текущее значение шага поиска.
Для решения конкретной задачи необходимо подготовить исходную информацию, которая состоит из наборов данных двух типов:
1) информация об именах используемых модулей и файлов;
2) входные наборы данных для решения одной или нескольких задач с фиксированными именами используемых модулей.
Структура модулей, вводимых пользователем:
Модуль MAIN
В модуле должны содержаться данные об общем числе алгоритмов библиотеки, а также о числе используемых алгоритмов, соответственно NALG и NAL. Номера используемых алгоритмов задаются присвоением элементам массива NVM (2,I) определённых чисел. Для вызова модуля M217 необходимо задать NVM (2,I)=7, для вызова модуля M211 – NVM (2,I)=1 и т.д. При решении задачи оптимизации динамической системы значение элемента NVM (1,1)=2. В случае статического объекта оптимизации – NVM (1,1)=1.
Реализация различных правил выбора алгоритмов оптимизации осуществляется путём присваивания элементу К222 определённых значений:
1) К222=1 – выбор алгоритма оптимизации в зависимости от поисковой ситуации;
2) К222=2 - выбор алгоритма оптимизации «по опыту» (детерминированный подход);
3) К222=3 – выбор алгоритма случайным образом;
4) К222=4 – выбор алгоритма по заданию пользователя. Только в этом случае NVM (2,I)≠0.
Далее следует обращение к модулю ввода исходных данных M20 и управляющей программе M2.
Модуль MAIN заканчивается операторами STOP и END.
Модуль M200
Модуль служит для формирования исходной точки оптимизации. В нём задаются начальные значения вектора независимых переменных XT(I), вектора предпочтительного направления W(I), масштабных коэффициентов DEX(I) и др.
Здесь же задаются коэффициенты К271, К272, необходимые для вычисления приращений независимых переменных  , используемых при расчёте
, используемых при расчёте  . Задание вектора независимых переменных XT(I) может и отсутствовать, если осуществляется работа последовательности программ оптимизации. Причём, начальная точка для первой программы задаётся пользователем в М20, для последующих программ начальной служит результирующая точка предыдущей программы.
. Задание вектора независимых переменных XT(I) может и отсутствовать, если осуществляется работа последовательности программ оптимизации. Причём, начальная точка для первой программы задаётся пользователем в М20, для последующих программ начальной служит результирующая точка предыдущей программы.
Модуль М210
Модуль служит для оперативного изменения параметров алгоритмов оптимизации, исходные значения которых содержатся в BLOCK DATA. Для изменения параметров соответствующего алгоритма с порядковым номером, например, 5 (имя модуля М215), необходимо использовать условный оператор перехода вида.
IF (KEYM.EQ.5) GOTO 5
и начиная с метки 5 вставить операторы присвоения параметрам алгоритма соответствующих численных значений. Операция присвоения заканчивается оператором RETURN.
Входные данные по задаче (данные II типа) могут размещаться во входном наборе данных, имя которого содержится в определённом операторе ввода данных READ. Как уже указывалось, ввод исходных данных к задаче оптимизации (N, X(I), JCN, JCP и т.д.) осуществляет модуль М20.
Сначала осуществляется ввод целочисленных переменных N, JCN, JCP, K1. Далее осуществляется ввод массива независимых переменных X(I), где I изменяется от 1 до N1, N1=3N. Первые N элементов массива соответствуют координатам исходной точки  , следующие N элементов – верхние ограничения
, следующие N элементов – верхние ограничения  на независимые переменные, последние N элементов – нижние ограничения
на независимые переменные, последние N элементов – нижние ограничения 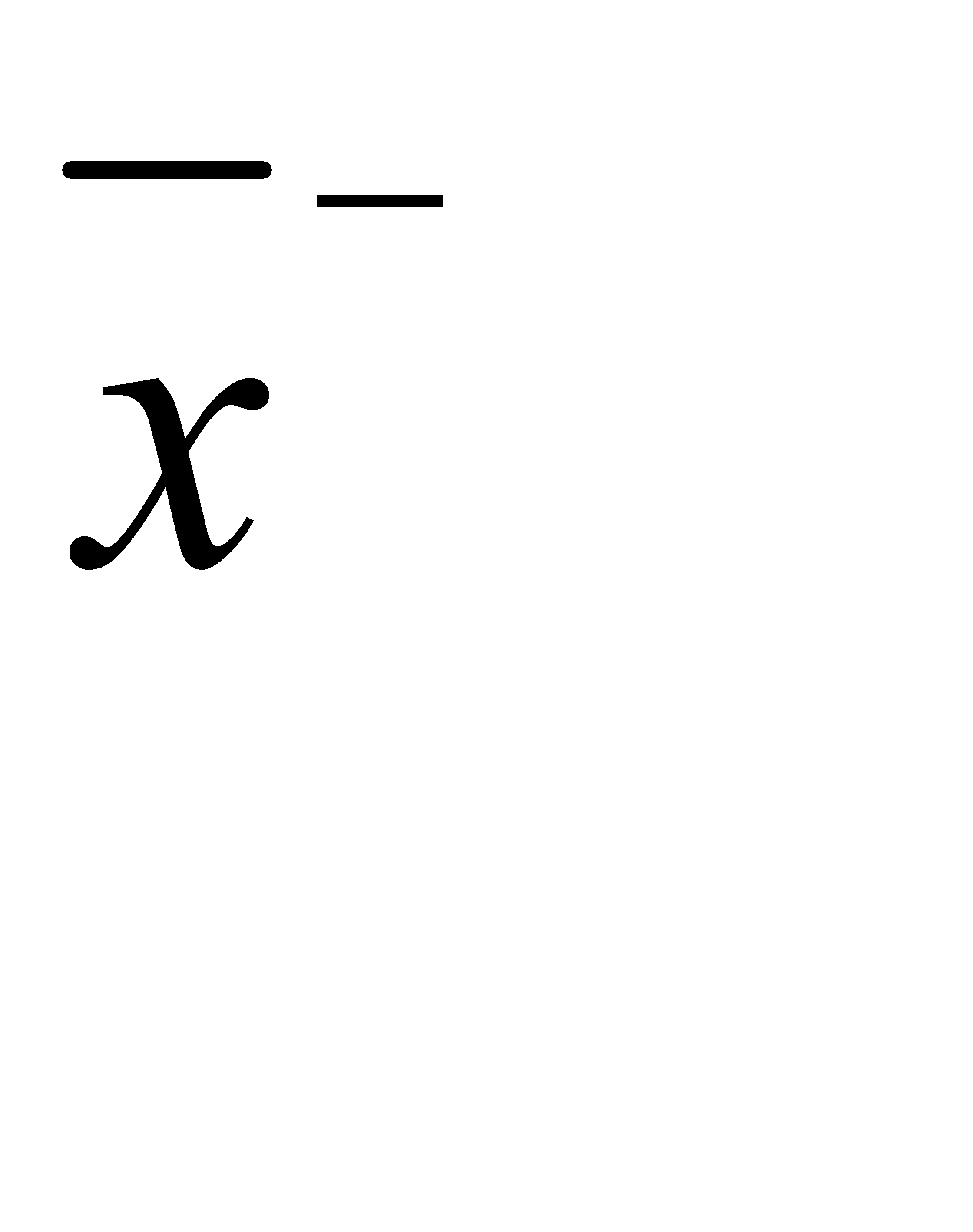 на независимые переменные.
на независимые переменные.
Для решения конкретной задачи оптимизации помимо вышеуказанной исходной информации необходимо составить подпрограмму вычислений критерия оптимальности  . Подпрограмма должна иметь заголовок SUBROUTINE M3. Значение аргумента X, для которого вычисляется критерий оптимальности Q, передаётся в подпрограмму с помощью оператора COMMON/A2/X(150), Q
. Подпрограмма должна иметь заголовок SUBROUTINE M3. Значение аргумента X, для которого вычисляется критерий оптимальности Q, передаётся в подпрограмму с помощью оператора COMMON/A2/X(150), Q
Например, для оптимизируемой функции 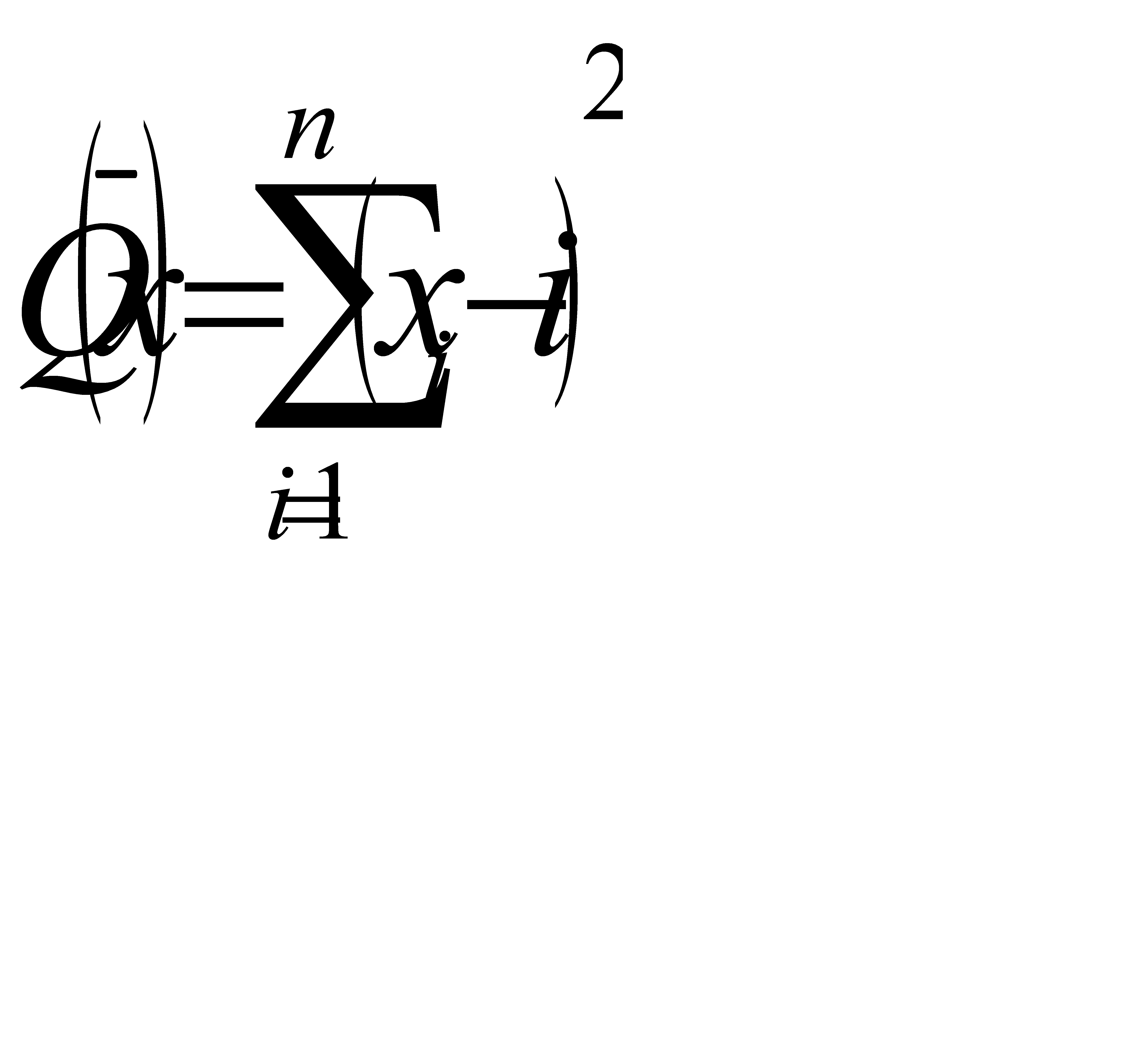 подпрограмма М3 имеет вид:
подпрограмма М3 имеет вид:
SUBROUTINE M3
COMMON/A2/X(150),Q
COMMON/H2/N
Q1=0.
DO 2 I=1,N
Q1=Q1+(X(I)-I)**2
2 CONTINUE
Q=Q1
RETURN
END
| M211A |
– модуль реализует алгоритм случайного поиска (Растригин - Рипа)
Для обмена данными с вызывающими и вызываемыми модулями в М211А содержатся следующие операторы:
COMMON/A2/ X(150),Q
COMMON/B211/ JCN, JCP, EPSD, EPSQ, DX, DXMIN, G1, G2, K1, R8
COMMON/C2/ X0(50), DEX (50)
COMMON/D2/ BX(50), XB(50), XT(50)
COMMON/E2/ RAN(50), KEYR
COMMON/F2/ QN1, QN2, QN
COMMON/G2/ JC4, JC5, JC5
COMMMON/H2/ N
Помимо вышеописанных операторы содержат следующие переменные:
QN1, QN2 – текущие значения критерия качества;
X0(50) – координаты начальной точки  ;
;
RAN(50) – массив случайных чисел, распределённых по равномерному закону в интервале [-1, 1] в модуле М28;
KEYR – ключ, задающий вариант формирования RAN(50);
BX(50), XB(50) – текущие значения независимых переменных.
Используемые подпрограммы:
М3, М721, M722, M28, M25, M29, M24
Аналогичные операторы содержатся и в других модулях пакета, реализующих те или иные алгоритмы оптимизации.
4.6 Состав библиотеки методов оптимизации
На основе сопоставительного анализа методов оптимизации, изложенного в литературе, произведен выбор эффективных, достаточно просто реализуемых алгоритмов. Библиотека методов оптимизации насчитывает порядка 20 поисковых процедур, предназначенных для работы в различных ситуациях. Рассматриваемые в работе методы безусловной оптимизации могут быть классифицированы следующем образом:
1) Прямые методы случайного поиска, которые используют только значения функции  ;
;
2) Градиентные методы первого порядка, которые используют значение функции и ее производных;
3) квазиньютоновские методы;
4) Овражные методы поиска;
5) Методы поиска глобального экстремума.
При решении задачи оптимизации неунимодальной целевой функции, помимо методов поиска глобального экстремума, могут быть использованы методы, перечисленные в пп. 1-4, а начальная точка 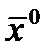 формируется в модуле М200 с помощью датчика псевдослучайных чисел:
формируется в модуле М200 с помощью датчика псевдослучайных чисел:

Где  - псевдослучайное число, равномерно распределенное в интервале (-1; 1);
- псевдослучайное число, равномерно распределенное в интервале (-1; 1);
j-1, j – номера этапов поиска.
Ниже приведен перечень программных модулей второго уровня, реализующих вышеуказанные методы оптимизации (см. таблицу 4.1)
Состав библиотеки методов оптимизации
Таблица 4.1
| № | Имя модуля библиотеки | Метод оптимизации реализованный в модуле | № | Имя модуля библиотеки | Метод оптимизации, реализованный в модуле |
| М211А | Случайный поиск с адаптацией (Растригин – Тарасенко) | М2191 | Наискорейший спуск | ||
| М211А | Случайный поиск с самообучением (Келли – Уиллинг) | М21171 | Статистический градиент с адаптацией шага по распределению Джонсона (Волынский – Филатов) | ||
| М2141 | Случайный поиск с самообучением (Растригин – Рипа) | М21161 | Случайный поиск с регулируемой величиной спуска | ||
| М2151 | Случайный поиск с самообучением (Даниленко – Каган) | М21131 | Метод оврагов (Павлов – Солдатов) | ||
| М2171 | Случайный поиск с самообучением (Трахтенберг) | М2131 | Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов | ||
| М21101 | Случайный поиск со смешанной тактикой | М21181 | Локально – глобальный поиск коллективом автоматов Буша – Мостселлера | ||
| М21151 | Экстраполяционный случайный поиск с адаптацией шага | М2111 | Метод Давидона - Флетчера | ||
| М21161 | Случайный метод с перестройкой вероятностных характеристик поиска (Севриткин) | М2112 | Метод сопряженных градиентов | ||
| М21141 | Градиентный метод |
Далее приведен перечень стандартных программ для решения задач нелинейного программирования. При разработке программ, рассчитанных на решения некоторого класс задач различными методами, важными представляются вопросы стандартизации обращения к этим программам. Стандартное обращение позволяет легко при необходимости заменить одну программу на другую, использовать имена программ в качестве параметра при конструировании другой программы. В таблице 4.2 приведен перечень программ безусловной минимизации, имеющихся в пакете научных программ SSP. Все многообразие реализованных в этих программах методов может быть разделено на следующие группы:
1) Методы нулевого порядка;
2) Методы первого порядка;
3) Методы второго порядка;
4) Методы случайного поиска;
Для того, чтобы воспользоваться этими программами, пользователю необходимо составить подпрограмму вычисления значений  и, при необходимости ее производных (в случае использования методов первого и второго порядков).
и, при необходимости ее производных (в случае использования методов первого и второго порядков).
Перечень стандартных программ оптимизации
Таблица 4.2
| № | Имя стандартной программы | Метод оптимизации, реализованный в программе | № | Имя стандартной программы | Метод оптимизации, реализованный в программе |
| MIN01 | Метод прямого поиска (Хук и Дживс) | MIN14 | Метод Давидона – Флетчера - Пауэлла | ||
| MIN02 | Метод пкордигнатного спуска | MIN15 | Метод сопряженных градиентов | ||
| MIN03 | Метод деформирующего многогранника (Нелдер и Мид) | MIN16 | Квазиньютоновский метод | ||
| MIN04 | Метод Розенброка | MIN21 | Метод Ньютона | ||
| MIN05 | Метод Пауэлла | MIN31 | Случайный метод с пересчетом и метод наилучшей пробы | ||
| MIN06 | Квазиньютоновский метод с аппроксимацией производных при помощи разностей | MIN0A | Гибридные алгоритмы | ||
| MIN07 | Метод Пшеничного - Редковского | MIN0B | |||
| MIN11 | Наискорейший спуск | MIN22 | Двухпараметрический метод второго порядка |
Если используются градиентный метод или метод наискорейшего спуска, то необходимо иметь подпрограмму, вычисляющую значения первых производных критерия оптимизации. В пакете для этих целей служит подпрограмма
SUBROUTINE M27 (N, XG, QG, SG)
где XG – массив текущих значений аргументов оптимизируемой функции;
QG – текущее значение оптимизируемой функции;
SG – массив текущих значений градиента функции;
Подпрограмма M27 имеет вид:
SUBROUTINE M27 (N, XG, QG, SG)
COMMON/A2/X(150), Q
COMMON/B219/NNG, DLX(50)
COMMON/B27/K271, K272
REAL K271, K272
DIMENSION SG(N), XG(N)
DO 3 I=1, N
X(I)=XG(I)
3 CONTINUE
CALL M3
QG=Q
S=0
DO 2 I=1, N
DLX(I)=K271+K272*(ABS(XG(I)))
X(I)=X(I)+DLX(I)
CALL M3
QN1=Q
SG(I)=(QN1-QG)/DLX(I)
X(I)=X(I)-DLX(I)
2 CONTINUE
RETURN
END
Точность вычисления градиента регулируется коэффициентами К271 и К272 в формуле для пробных перемещений DLX(I) в пространстве независимых переменных.
4.7 Критерии останова, аварийные ситуации,
вывод на печать результатов счёта
Критерием останова для каждой программы минимизации служит одновременное выполнение N раз подряд следующих условий:
 (4.1)
(4.1)
 (4.2)
(4.2)
где  ,
, 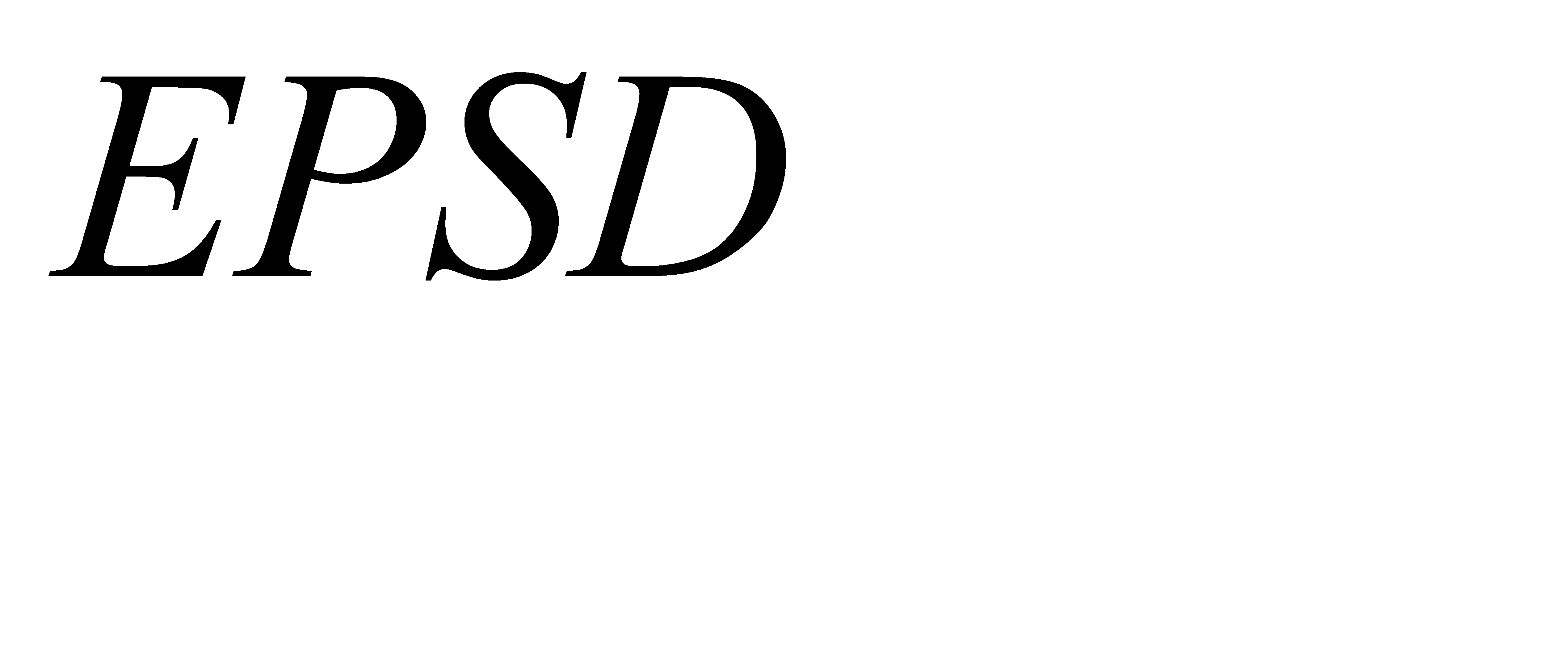 ,
, 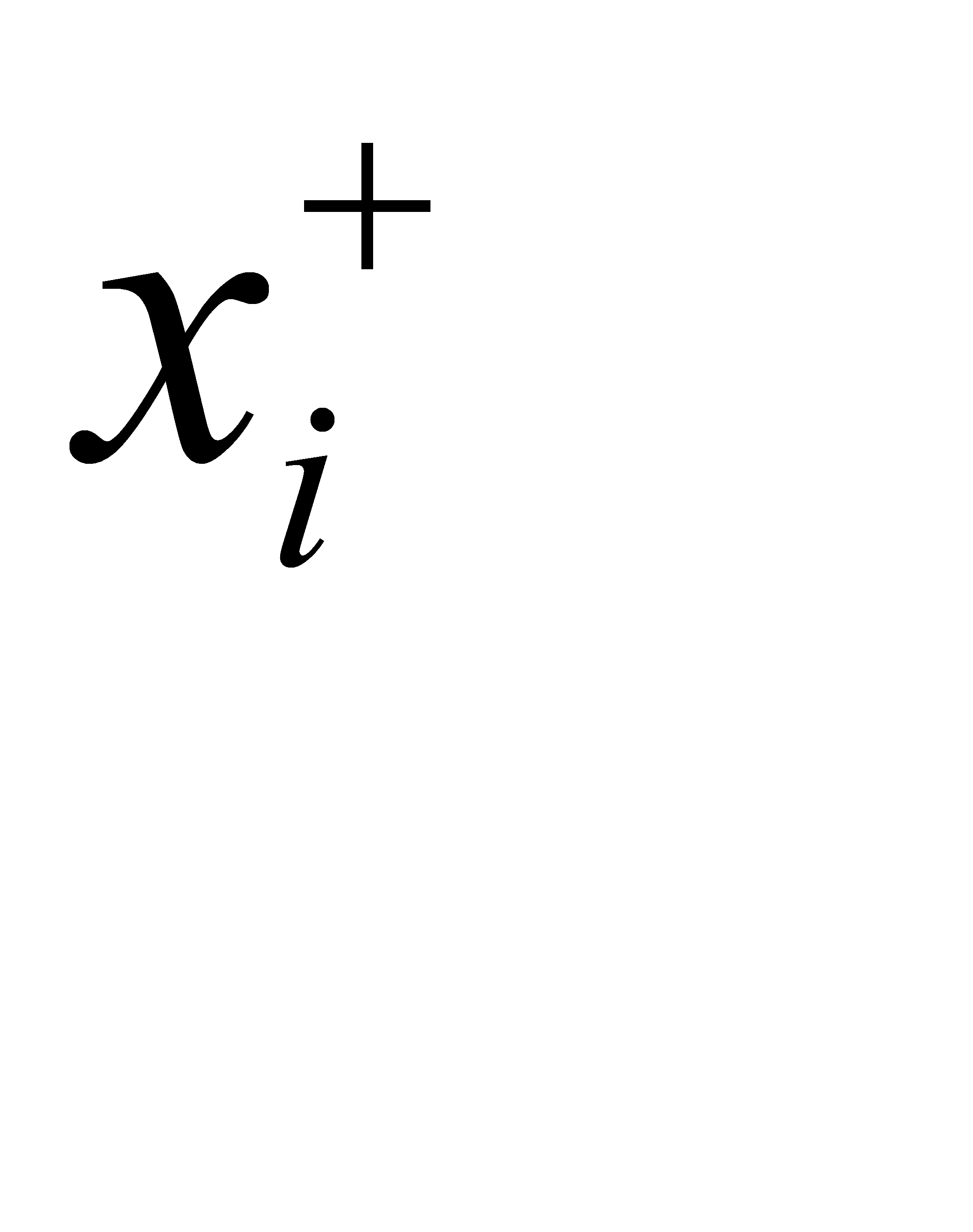 ,
,  - входные параметры
- входные параметры
 ,
,  - текущие значения независимых переменных и критерия оптимальности на k -ой итерации;
- текущие значения независимых переменных и критерия оптимальности на k -ой итерации;
 ,
,  - текущие значения независимых переменных и критерия оптимальности на (k-1) итерации;
- текущие значения независимых переменных и критерия оптимальности на (k-1) итерации;
Независимо от выполнения вышеуказанных условий, пакет программ оптимизации закончит свою работу в случае исчерпания ресурса JM2, т.е. если JC6>JM2. В этом случае IER=8, в отличие от вышеприведённых условий (4.1), (4.2), когда IER=6.
Возможны также остановы в аварийных ситуациях:
1) Начальная точка, задаваемая пользователем, лежит вне области определения. В этом случае IER=16 и печатается сообщение «Начальная точка x(I) – вне области поиска».
2) За K4 вычисления функции качества число неудачных шагов поиска JC4 превысило число удачных шагов JC2. в этом случае IER=10.
3) Количество вычислений  превысило допустимое значение JCN, задаваемое пользователем. В этом случае IER=7.
превысило допустимое значение JCN, задаваемое пользователем. В этом случае IER=7.
При останове по любой из этих причин работа комплекса заканчивается и управление через оператор RETURN передаётся в вызывающую программу M2. Если не исчерпан ресурс по числу итераций, то начинается работа следующей процедуры оптимизации.
Вывод на печать результатов работы процедур оптимизации производится в соответствии с входными параметрами через JCP итераций. На печать выводится:
JC6, JC4, JC2 – соответственно общее число неудачных и удачных шагов поиска;
QN – значение функции качества, минимальное за JC6 шагов поиска;
XT(I) – массив текущих значений независимых переменных, соответствующих QN;
DX – текущее значение шага поиска.
Печать вышеуказанных переменных осуществляется процедурой M7221. В последнем пользователь может вывести на печать дополнительные переменные, характеризующие процесс поиска и передаваемые в M7221 через COMMON - область.
Управление печатью можно осуществить в M7221 с использованием параметра IPR, как это, например, сделано в [8 ].
5. Примеры практического применения
алгоритмов поисковой оптимизации
Целью создания систем автоматизированного оптимального проектирования является улучшение качества проектируемых технических систем, сокращение сроков их разработки и освоения их в производстве.
Система оптимального проектирования представляет собой сложную систему, включающую комплекс программных средств, информационную базу и др. Учитывая сложность структуры системы и её компонентов, необходимо после отладки многочисленных программных модулей проведения проверки работоспособности алгоритмов оптимизации на тестовых функциях, а также решение ряда практических задач оптимального проектирования.
Результаты такой работы позволяют оценить правильность принятых предпосылок относительно структуры системы, произвести сопоставительный анализ методов оптимизации, дать ряд практических рекомендаций по использованию методов оптимизации.
В данном разделе помимо тестовых проверок программ оптимизации рассмотрены некоторые задачи, возникающие, например, при проектировании автономных энергосистем, автоматически регулируемых по частоте и напряжению.
Для большинства практических задач создание математических моделей реальных систем является весьма сложным процессом, составляющим предмет самостоятельного исследования [9, 10 ]. Поэтому задачи рассматриваются в таком плане, чтобы без излишних подробностей изложить суть дела, проиллюстрировать трудности, возникающие при решении практических задач и, в некотором смысле, дополнить проведённое выше обсуждение методов оптимизации.
5.1 Тестовые результаты работы программ оптимизации
В данном разделе приведён анализ тестовых проверок алгоритмов оптимизации.
В качестве тестовых использовались функции, наиболее часто встречающиеся в литературе [4, 6, 8, 16, 34].
Эти функции подобраны так, чтобы они были «трудными» для методов оптимизации и хорошо служили для указания специфических особенностей конкретного метода. Эти функции используются как стандарт при сравнении методов оптимизации.
Успех машинного проектирования во многом определяется выбором поискового метода. Этот выбор обуславливается природой задачи: степенью нелинейности, топологией гиперповерхностей, размерностью и т.д. Эффективность поиска в не меньшей мере зависит от «деталей» алгоритма и машинной программы.
Небольшие изменения в процедурах выбора направления и величины шага поиска, параметров адаптации и самообучения могут изменить конечный результат поиска. Для выбора известных и разработки новых алгоритмов, для исследования их работоспособности целесообразно использование тестовых функций, которых в настоящее время предложено большое количество.
К алгоритмам поиска обычно предъявляются ряд требований. Они, по возможности, должны иметь высокую скорость, точность сходимости, надёжность.
Алгоритмы поиска должны легко реализовываться на ЭВМ, требовать минимальный объём памяти. Предварительная поисковая работа должна быть минимальной. Нас в сопоставительном анализе будет интересовать скорость и точность сходимости поиска.
Ниже в таблицах приведены результаты оптимизации тестовой функции вида  различными поисковыми методами.
различными поисковыми методами.
Выбор методов для сопоставительного анализа определялся, в основном, имеющимся программным обеспечением ЦВМ. Использовался ряд программ оптимизации, позволяющих находить локальные экстремумы функций. К ним относятся стандартная процедура нахождения экстремума функции методом градиента, методом случайного поиска, процедура отыскания минимума функций многих переменных. В последней процедуре запрограммированы следующие методы отыскания минимума функции  :
:
1) метод параллельных касательных;
2) метод наискорейшего спуска;
3) метод Гаусса – Зейделя;
4) метод конфигураций;
5) метод квадратичной аппроксимации.
В расчётах, результаты которых приведены ниже принимались:
1) размерность задачи n=10;
2) начальные значения независимых переменных  =100;
=100;
3) начальный шаг поиска  =100;
=100;
4) границы области поиска  .
.
Результаты тестовых проверок представлены в таблицах, где использованы обозначения:
N, J – число вычислений функции качества  ;
;
 - найденное экстремальное значение функции;
- найденное экстремальное значение функции;
 - вектор оптимальных значений независимых переменных.
- вектор оптимальных значений независимых переменных.
Результаты расчётов показали, что высокой скоростью сходимости обладает метод наискорейшего спуска. Очень низкая скорость сходимости у метода случайного поиска.
Таблица 5.1
Результаты оптимизации тестовой функции методом градиента
| Оптимизируемая функция | Число шагов | Независимые переменные | |||||||||

| J | 
| 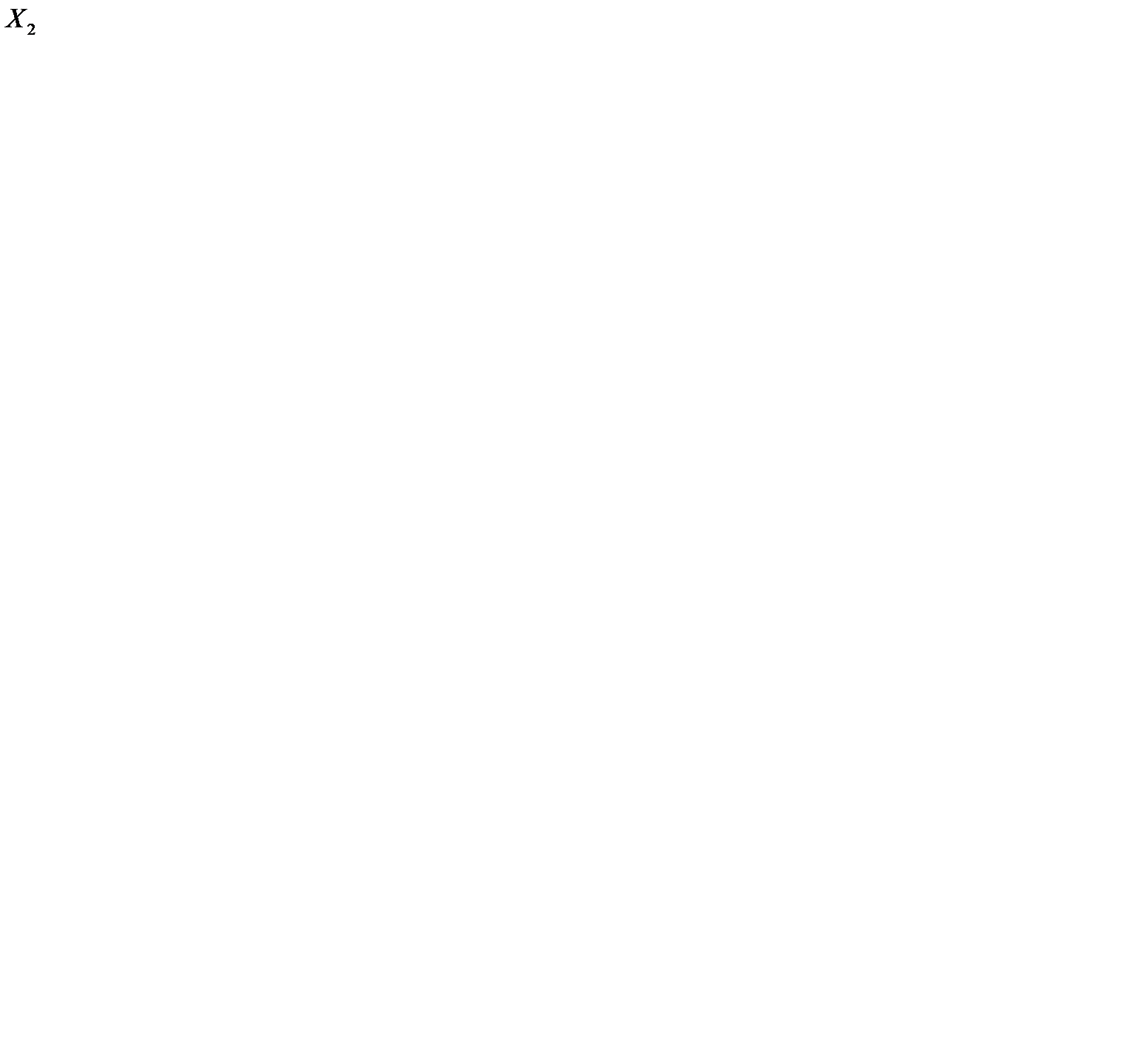
| 
| 
| 
| 
| 
| 
| 
| 
|
| – | |||||||||||
| 86,75 | 86,89 | 87,02 | 87,16 | 87,3 | 87,42 | 87,56 | 87,69 | 87,82 | 87,96 | ||
| 70,2 | 70,5 | 70,8 | 71,1 | 71,4 | 71,7 | 72,0 | 72,3 | 72,62 | 72,91 | ||
| 56,95 | 57,4 | 57,82 | 58,26 | 58,7 | 59,13 | 59,56 | 60,0 | 60,43 | 60,87 | ||
| 40,4 | 41,0 | 41,6 | 42,2 | 42,8 | 43,42 | 44,01 | 44,61 | 45,21 | 45,81 | ||
| 4557,7 | 23,84 | 24,61 | 25,38 | 26,15 | 26,92 | 27,69 | 28,46 | 29,22 | 30,0 | 30,77 | |
| 839,6 | 10,59 | 11,5 | 12,41 | 13,3 | 14,21 | 15,11 | 16,01 | 16,92 | 17,82 | 18,72 | |
| 0,1614 | 0,867 | 1,868 | 2,87 | 3,87 | 4,87 | 5,87 | 6,87 | 7,88 | 8,88 | 9,88 | |
| 0,000124 | 0,997 | 1,997 | 2,997 | 3,297 | 4,995 | 5,996 | 6,996 | 7,996 | 8,996 | 9,996 |
Таблица 5.2
Результаты оптимизации тестовой функции
методом случайного поиска
| Оптимизи- руемая функция | Число шагов | Независимые переменные | |||||||||

| J | 
| 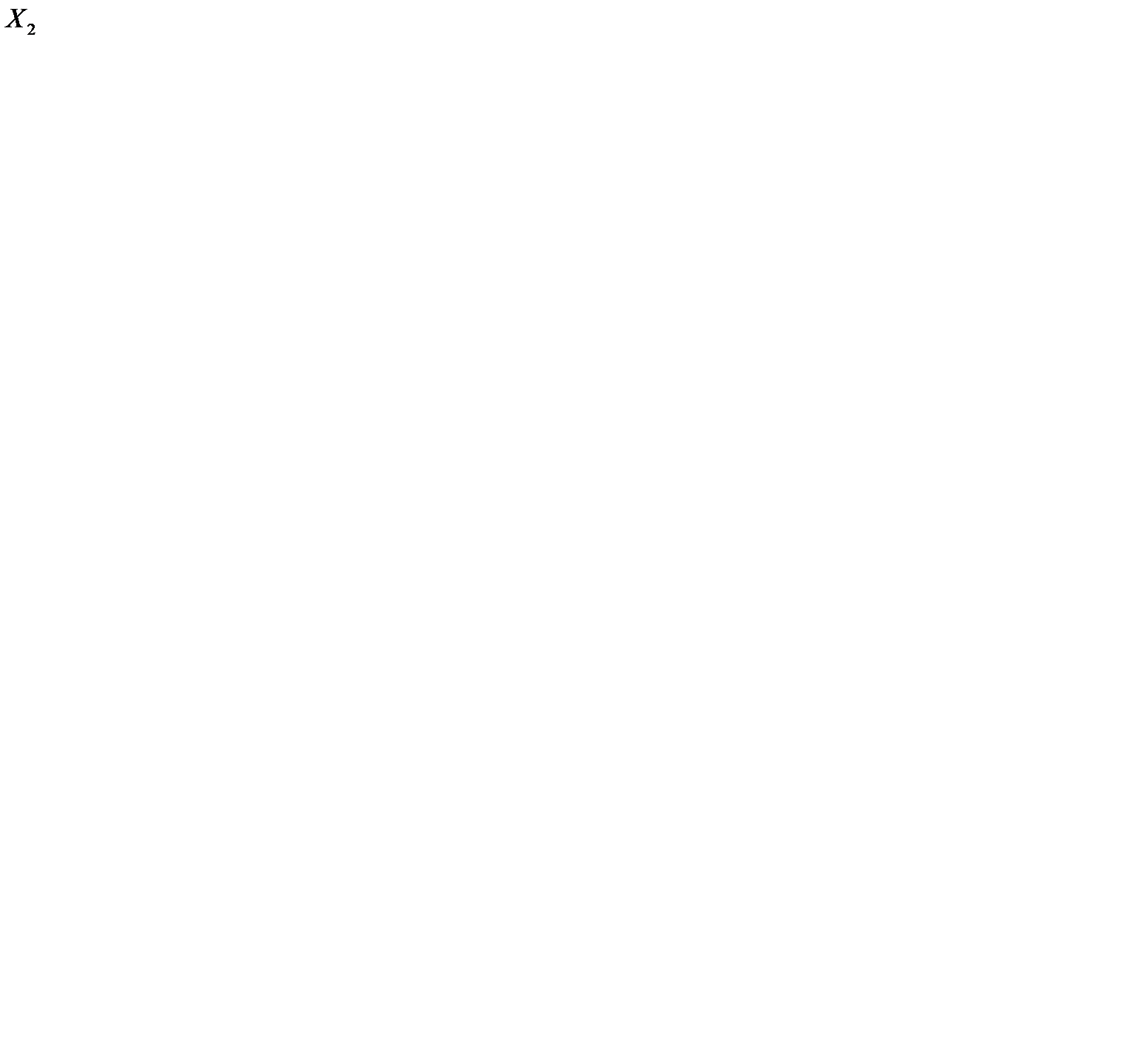
| 
| 
| 
| 
| 
| 
| 
| 
|
| – | |||||||||||
| 172,40 | 1,421 | 1,498 | 0,1 | 0,1 | 0,1 | 1,804 | 1,88 | 8,72 | 0,1 | 10,87 | |
| 14,65 | 2,028 | 3,391 | 0,870 | 3,587 | 4,34 | 4,371 | 6,339 | 6,625 | 8,737 | 8,787 | |
| 4,775 | 1,871 | 3,571 | 3,374 | 3,983 | 4,834 | 6,507 | 7,354 | 7,22 | 9,62 | 9,8 | |
| 0,3188 | 1,001 | 1,955 | 3,153 | 3,587 | 5,003 | 5,783 | 6,824 | 7,897 | 8,944 | 10,175 | |
| 0,1251 | 0,9672 | 2,013 | 3,036 | 3,741 | 4,884 | 5,965 | 7,095 | 8,071 | 8,873 | 10,103 |
Не нашли, что искали? Воспользуйтесь поиском: