Выбор независимых переменных 9 страница

Рассмотренные ниже примеры использования численных методов оптимизации для вычисления значения оптимизируемого показателя используют программы моделирования проектируемой системы.

В данном разделе ставится вопрос об улучшении динамических показателей сложных нелинейных систем (к каким относятся, например, автономные системы электроснабжения (АСЭ)) на основе применения методов нелинейного программирования (НЛП). В условиях широкого внедрения АСЭ[9,10] в народное хозяйство и возрастания требований к качеству электроэнергии актуальность подобных исследований не подвергается сомнению.

Основным источником электроэнергии в АСЭ является синхронный генератор (СГ), работа которого связана с процессами коммутаций нагрузок, изменений скорости первичного двигателя и т.д. Поэтому при проектировании СГ наряду с требованиями к габаритам, конструкции и т.д. предъявляется ряд требований и к динамическим показателям.

В настоящее время порядка 50% электроэнергии в АСЭ расходуется на электропривод различных механизмов, в качестве привода в которых широко используется асинхронные двигатели (АД). Объём выпускаемых высокоскоростных двигателей повышенной частоты с каждым годом растёт и является весьма перспективным. Поэтому проблема улучшения энергетических показателей и динамических свойств этих двигателей приобретает важное значение.

В последние годы для оптимального проектирования электрических машин общего и специального применения стали разрабатываться автоматизированные системы проектирования [2, 22, 23, 33], в которых актуальна, как уже указывалось, задача выбора алгоритма оптимизации, адекватного решаемой задаче, её размерности, "топологии" и т.д. Вообще говоря, для выбора известных и разработки новых алгоритмов, для исследования их работоспособности имеются тестовые функции. Однако, несмотря на большое разнообразие тестовых функций, они не могут в полной мере отразить содержание задач оптимального проектирования электрических машин.

Поэтому предметом рассмотрения в данном разделе, является оценка работоспособности поисковых алгоритмов в задачах оптимального проектирования электрических машин с учётом динамических свойств.

Оптимальное проектирование электрических машин с учётом динамических свойств осуществляется как случайными, так и детерминированными методами НЛП. В сопоставительном анализе решения задач НЛП к поисковым методам предъявляется ряд требований: скорость, точность сходимости, надёжность отыскания оптимального решения, простота реализации метода на ЦВМ и др. Нас будет интересовать скорость (число вычислений функции качества ) при заданной точности сходимости поиска.

5.2.1 Оптимальное проектирование асинхронного двигателя (АД)

Математическая модель АД известна [88]. В работе рассматривается оптимизация переходных процессов по току статора АД, для количественной оценки которых введены показатели: максимальный 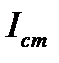и установившийся токи, время пуска двигателя . Проведённые ранее исследования подтверждают гипотезу о существенности влияния выбранных показателей на качество переходных процессов по напряжению U и частоте f - основным регулируемым координатам в АСЭ.

При разработке регуляторов напряжения и частоты в АСЭ наиболее важным динамическим показателем является время пуска двигателей. Целесообразным является также наложение ограничений на максимальные статорные токи двигателей. В качестве оптимизируемых приняты следующие параметры АД:

- активное и индуктивное сопротивление рассеяния статора;

- активное сопротивление ротора;

- активное сопротивление реакции статора;

- момент инерции ротора.

На базе методов планируемого эксперимента [86], получена полиномиальная модель, позволяющая установить непосредственную связь между критериями качества и параметрами объекта исследования:

Для получения зависимостей (5.5) используется стандартная процедура [ 86], позволяющая рассчитать коэффициенты , , и оценить адекватность аппроксимирующих выражений (5.5).

Поставленная задача сводится к минимизации функции

при ограничениях

Для расчёта коэффициентов зависимостей (5.5) используется дробный факторный эксперимент типа ДФЭ с генерирующим соотношением . Интервалы варьирования параметров представлены в таблице 5.12 Коэффициенты аппроксимирующих выражений представлены в таблице 5.13.

Для преобразования исходной задачи на условный экстремум к задаче безусловной минимизации используется метод штрафных функций. В соответствии с этим методом находят последовательность точек вспомогательной функции

(5.6)

где

при последовательном увеличении коэффициента штрафа . При этом стремится к искомому решению .

Результаты поиска оптимальных параметров АД из условия минимального времени пуска приведены в таблицах 5.14 и 5.15. Максимальный и установившийся токи статора по условиям задачи не должны превышать 227А и 25А, т.е. тех значений, которые имеет двигатель при номинальных параметрах.

Варьируемые параметры асинхроннго двигателя

Таблица 5.12

Факторы	Параметры асинхронной машины	Уровни факторов	Интервал варьирования
нижний -1	верхний +1	нулевой 0
	- активное сопротивление статора, Ом	0.045	0.075	0.060	0.015
	- активное сопротивление ротора, Ом	0.090	0.150	0.120	0.030
	- инд. сопротивление реакции статора, Гн	3.60	6.00	4.80	1.20
	- инд. сопротивление рассеяния статора, Гн	0.18	0.30	0.24	0.06
	- момент инерции ротора,	0.003	0.0074	0.0052	0.0022

Коэффициенты полиномиальных моделей

Таблица 5.13

Функции отклика	Коэффициенты полиномов
	226.9	-2.30	-9.47	-1.83	-22.97	1.28	-0.03	1.27	0.57	-0.43	-0.5	3.36	1.76	0.53	0.02	-1.07
	25.18	-0.001		-6.0	-0.34			0.001	0.001				-0.001	0.15
	0.174	0.0037	-0.015	0.0025	0.026	0.071	0.0001	-0.0025	0.0012	0.0012	0.0012	-0.005	-0.005	-0.0001	0.0001	0.0112

Таблица 5.14

Метод поиска	Количество обращений	Координаты точки опт.	Значение критерия оптимизации	Значения ограничений
S=5	S=6	S=7	S=5	S=6	S=7	S=5	S=6	S=7	S=5	S=6	S=7
Метод параллельных касательных				-1.0000 +1.0000 +0.0303 -0.0016 -0.0080	-1.0000 +1.0000 +0.0303 -0.0016 -0.0080	-1.0000 +1.0000 +0.0303 -0.0016 -0.0080	0.1549	0.1549	0.1549	219.66	219.66	219.66
25.00	25.00	25.00
Метод наискорейшего спуска				-0.0020 +0.0083 +0.0328 -0.0125 -0.0394	-0.0039 +0.0161 +0.0314 -0.0257 -1.0000	-0.0039 +0.0161 +0.0314 -0.0257 -1.0000	0.1708	0.1025	0.1025	227.00	225.95	225.95
24.99	25.00	25.00
Метод Гаусса – Зейделя				-1.0000 +1.0000 +0.0387 -0.1315 -1.0000	-1.0000 +1.0000 +0.0387 -0.1315 -1.0000	-1.0000 +1.0000 +0.0387 -0.1315 -1.0000	0.0895	0.0895	0.0895	218.66	218.66	218.66
24.99	24.99	24.99
Метод конфигурации				-0.2288 +0.1548 +0.0302 -0.0016 -1.0000	-0.2296 +0.1555 +0.0302 -0.0018 -1.0000	-0.2303 +0.1563 +0.0302 -0.0026 -1.0000	0.1009	0.1009	0.1009	224.28	224.27	224.28
25.00	25.00	25.00
Метод квадратичной аппроксимаци				+0.8795 +0.9883 +1.0000 0.7618 -1.0000	-1.0000 +1.0000 +0.0588 -0.5058 -1.0000	-1.0000 +0.9998+0.0596 -0.5271 -0.9996	0.2485	0.2485	0.2485	203.20	229.17	226.45
27.18	23.02	25.99
Метод случайного поиска				+1.0000 +1.0000 +0.9945 -0.8931 -1.0000	+1.0000 +1.0000 +0.9945 -0.8931 -1.0000	+1.0000 +1.0000 +0.9945 -0.8931 -1.0000	0.0869	0.0869	0.0869	227.0	227.0	227.0
Критерий выхода из программы поиска

Таблица 5.15

Метод поиска	Количество обращений	Координаты точки опт.	Значение критерия оптимизации	Значения ограничений
S=5	S=6	S=7	S=5	S=6	S=7	S=5	S=6	S=7	S=5	S=6	S=7
Метод параллельных касательных				-1.0000 +1.0000 +0.0308 -0.0014 -0.0054	-1.0000 +1.0000 +0.0308 -0.0014 -0.0054	-1.0000 +1.0000 +0.0308 -0.0014 -0.0054	0.155	0.1551	0.1551	219.7	219.8	219.8
24.99	24.99	24.99
Метод наискорейшего спуска				-0.0043 +0.0275 +0.0318 -0.0292 -1.0000	-0.0043 +0.0375 +0.0318 -0.0292 -1.0000	-0.0043 +0.0475 +0.0318 -0.0292 -1.0000	0.102	0.1023	0.1022	226.0	225.9	225.8
25.00	25.00	25.00
Метод Гаусса – Зейделя				-1.0000 +1.0000 +0.0445 -0.1240 -1.0000	-1.0000 +1.0000 +0.0445 -0.1240 -1.0000	-1.0000 +1.0000 +0.0445 -0.1240 -1.0000	0.089	0.0896	0.0896	218.5	218.5	218.5
24.96	24.96	24.96
Метод конфигурации				-0.3293 +0.9006+0.8343 -0.1450 -1.0000	-0.9653 +0.9014 +0.3957 -0.3061 -1.0000	-0.8702 +0.8686 +0.3957 -0.4350 -1.0000	0.9	0.0943	0.1072	217.0	222.3	229.6
20.41	23.09	22.96
Метод квадратичной аппроксимации							0.123	0.1231	0.1231	208.53	208.53	208.53
28.45	28.45	28.45
Метод случайного поиска				+0.6163 +1.0000 +0.9915 -0.3540 -1.0000	+0.6163 +1.0000 +0.9915 -0.3540 -1.0000	+0.6163 +1.0000 +0.9915 -0.3540 -1.0000	0.107	0.1074	0.1074	194.2	194.2	194.2
18.99	18.99	18.99
Критерий выхода из программы поиска

Таблица 5.16

Критерий оптимизации	Значения ограничений	Значения критерия оптимизации и ограничений в точке оптимума	Координаты точки оптимума	Параметры объекта	Результаты расчёта переходных процессов объекта
			+1.0000 +1.0000 +0.9945 -0.8931 -1.0000
			+1.0000 +1.0000 +1.0000 +1.0000 -1.0000

Результаты расчётов, приведенные в таблице 5.14, показывают, что при заданной точности:

- наилучшее приближение к искомому решению дают методы случайного поиска, Гаусса-Зейделя, квадратичной аппроксимации;

- наименьшее число обращений к минимизируемой функции имеют методы Гаусса-Зейделя и наискорейшего спуска;

- наибольшее число обращений к минимизируемой функции имеют методы случайного поиска и квадратичной аппроксимации.

Результаты решения задачи при уменьшении точности поиска (табл. 5.15) позволяют к вышеуказанному добавить, что наилучшее приближение к искомому решению также имеет метод Гаусса-Зейделя, который имеет наименьшее число обращений к минимизируемой функции.

Аналогичным образом решается задача параметрического синтеза АД с точки зрения min при сохранении в прежних пределах времени пуска и установившегося значения тока статора. Параметры объекта, полученные в результате решения обеих задач оптимизации, приведены в табл.5.16.

Результаты решения задач оптимизации показывают, что варьируя параметры объекта (АД), можно добиться уменьшения времени пуска с до , а также снижения величины с 227А до 193,3А при сохранении в прежних пределах других показателей динамики.

В целях проверки достоверности полученных результатов, были рассчитаны переходные процессы запуска асинхронной машины от сети переменного тока напряжением U=120В и частотой f=400 Гц с использованием системы уравнений [88] и параметров (табл. 5.16). Расчеты показывают хорошее совпадение результатов вычислений по полиномиальной модели с результатами, полученными решением системы алгебро-дифференциальных уравнений объекта.

5.2.2 Оптимальное проектирование синхронного генератора (СГ)

Решение задачи оптимизации СГ по критерию качества переходных процессов позволяет [89]:

- наряду с применением оптимальных регуляторов оценить улучшение динамики АСЭ за счёт изменения параметров объекта регулирования;

- более обоснованно подходить к вопросам конструирования синхронных машин.

Исследовалась возможность улучшения качества переходных процессов в АСЭ с электромеханическим приводом постоянной скорости. Динамические свойства системы оценивались с помощью интегральной квадратичной оценки

где , - отклонения напряжения и частоты в АСЭ от установившихся значений;

, - весовые коэффициенты.

В качестве расчётных в АСЭ были выбраны режимы включения статической нагрузки номинальной мощности. Оптимизируемыми параметрами синхронной машины являлись:

- активное сопротивление и индуктивность рассеяния статорной обмотки;

Не нашли, что искали? Воспользуйтесь поиском: