
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Выбор независимых переменных 6 страница
Методы этой теории необходимы для представления показателей качества переходных процессов в виде полиномов, в которых аргументами являются исследуемые параметры системы.
Таким образом, применение теории планирования эксперимента позволяет относительно просто для сложных систем управления получить аналитические зависимости показателей качества динамических свойств системы от её параметров. Затем может решаться общая задача нелинейного программирования по выявлению параметров системы, обеспечивающих экстремум выбранных показателей качества.
Методы планирования эксперимента позволяют также сократить объём вычислений за счёт отсеивания тех параметров, изменение которых не даёт существенного изменения критерия оптимальности. С этой целью проводятся так называемые отсеивающие эксперименты. Если значение критерия оптимальности мало изменяется при изменении отдельных параметров на минимальном и максимальномуровнях, то соответствующие параметры временно исключаются из рассмотрения. В результате уменьшается размерность пространства поиска, что ускоряет движение к оптимуму. При этом после определённого числа шагов необходимо проверить, следует ли расширить пространство поиска введением ранее исключённых переменных [86].
Рассмотрим более подробно применение теории планирования эксперимента для представления показателей качества переходных процессов в полиномиальной форме:
 (3.9)
(3.9)
где  - исследуемые параметры системы;
- исследуемые параметры системы;
 - их основные уровни;
- их основные уровни;
 - интервал варьирования;
- интервал варьирования;
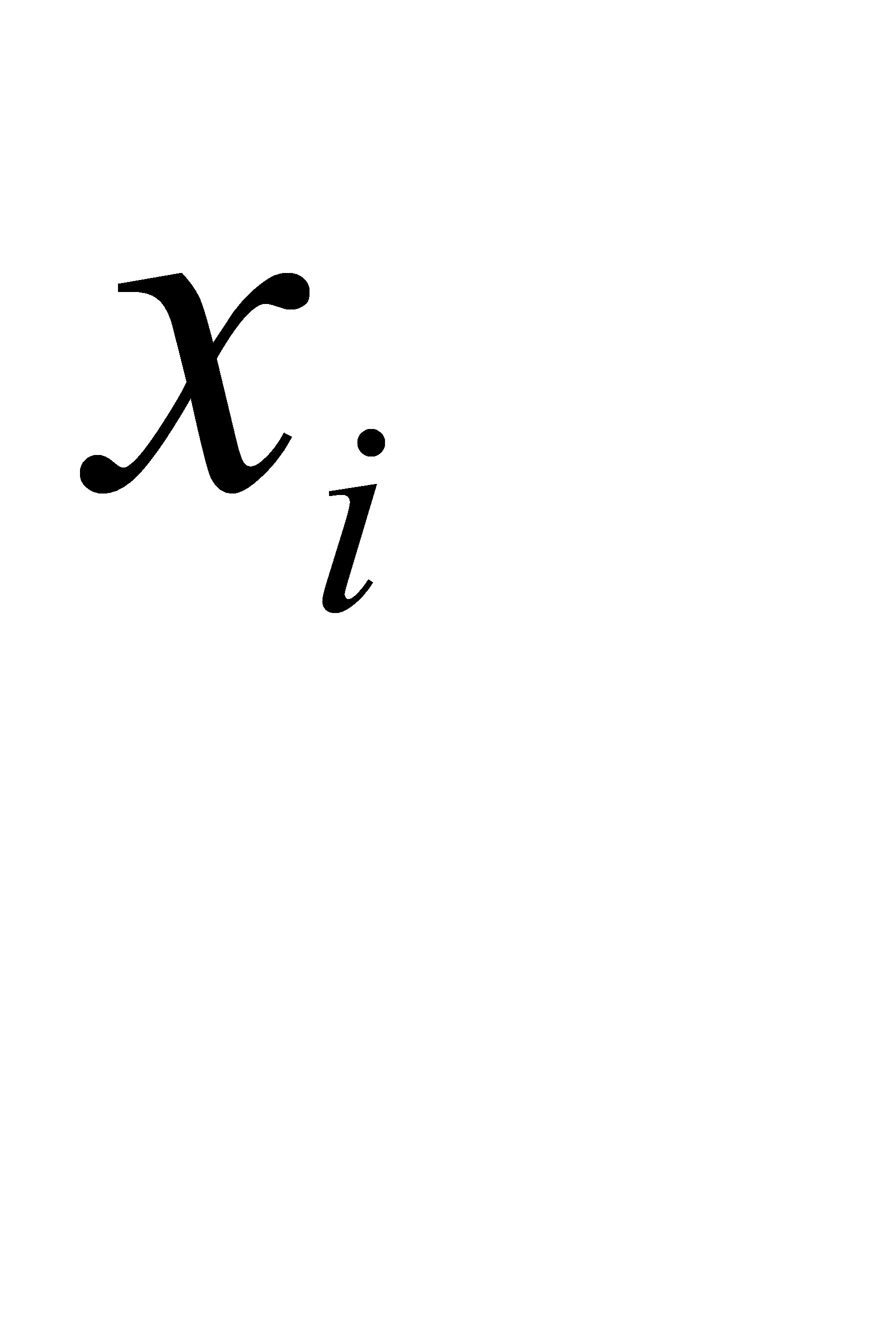 - те же параметры системы, но центрированные и масштабированные т.е. в относительных единицах (факторы) [86];
- те же параметры системы, но центрированные и масштабированные т.е. в относительных единицах (факторы) [86];
 - число параметров;
- число параметров;
 - коэффициенты.
- коэффициенты.
Применение планирования эксперимента предусматривает искусственное варьирование параметров системы по матрице планирования и практически возможно только на моделях. К параметрам планирования можно отнести количество переменных, интервал варьирования, основные уровни и величину звёздного плеча для планирования второго порядка [86].
После расчёта коэффициентов полиномиальной модели, полученные в результате обработки результатов расчётов, выполненных в соответствии с выбранными параметрами и матрицей планирования по стандартной процедуре, полиномиальная модель подвергается анализу на адекватность. При использовании теории планирования эксперимента для преобразования сложных исходных математических моделей возникают особенности в проверке адекватности полиномиальной модели и оценке значимости коэффициентов уравнения (3.9), связанные с отсутствием дисперсии воспроизводимости. В настоящее время создано несколько приёмов, позволяющих выйти из этого затруднительного положения. Наиболее простым приёмом является введение искусственной дисперсии опытов [87]

где  .
.
Если модель неадекватна, то, используя приёмы повышения адекватности (уменьшения интервалов варьирования, смещения основных уровней и др.), необходимо добиться адекватности модели.
Адекватность полиномиальной модели зависит о многих факторов, таких как сложность математического описания исходной системы, выбранного плана исследования, интервалов варьирования и др. Исследования показывают, что при использовании цифровых моделей транспортных электроэнергетических систем, линейные модели, как правило, неадекватны. Эти системы достаточно точно могут быть описаны полиномами второй степени при интервале варьирования  от основного уровня.
от основного уровня.
Не останавливаясь более подробно на проблеме адекватности модели [86] рассмотрим процесс оптимизации при условии, что полиномы (3.9) адекватно описывают процессы в исследуемых системах.
При исследовании транспортных энергосистем задача оптимизации, как и ранее, формируется как задача нелинейного программирования, однако с целевыми функциями и ограничениями, заданными в аналитической форме со степенью сложности полиномиальной модели не выше двух.
Исследования [87] показывают, что композиция методов планирования эксперимента и методов случайного поиска для оптимального проектирования систем повышает эффективность исследования. Дело в том, что для повышения сходимости алгоритма случайный шаг определяется зависимостью
 , (3.10)
, (3.10)
где 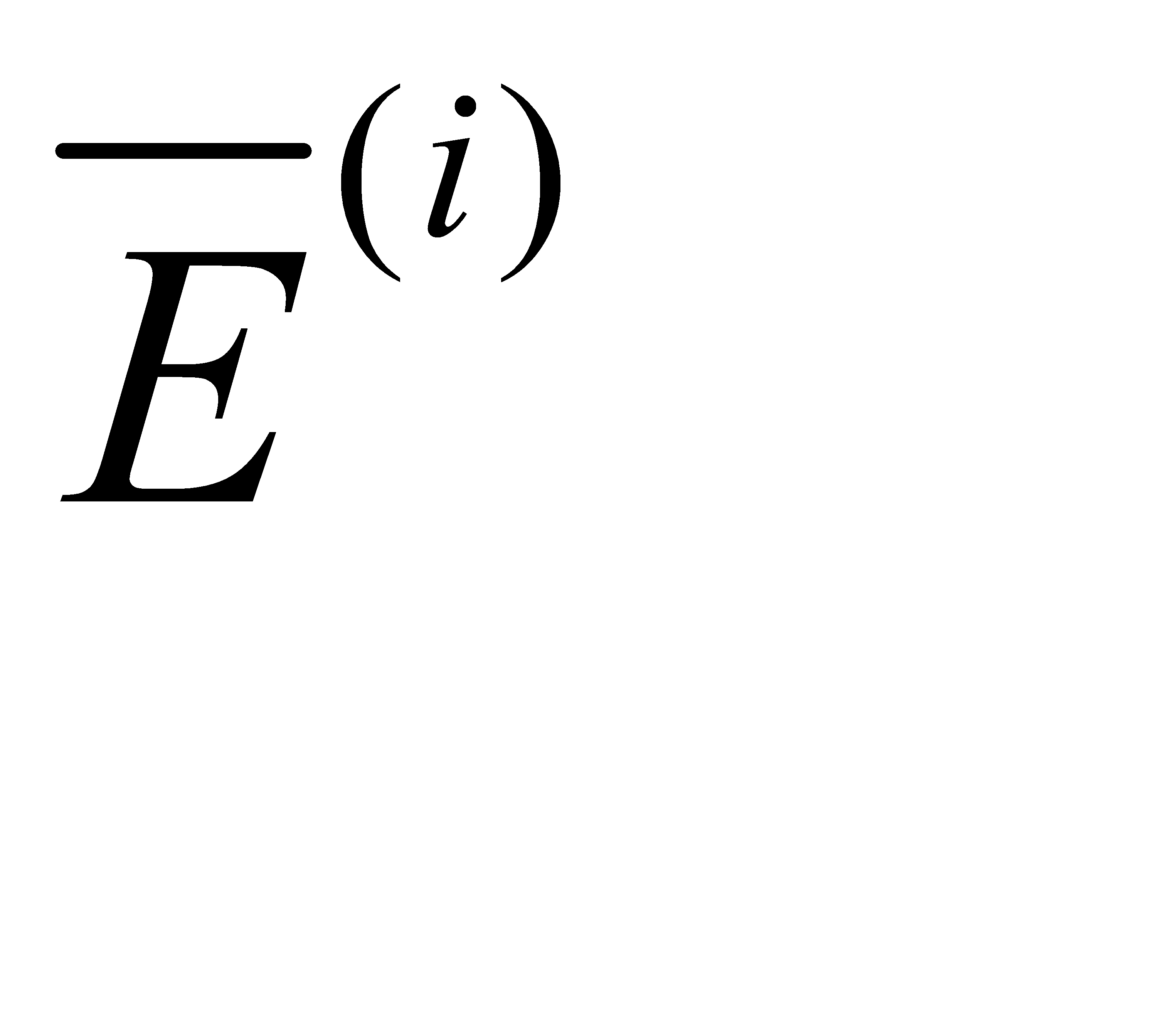 - реализация случайного вектора, компоненты которого распределены по равномерному закону в интервале [-1; 1].
- реализация случайного вектора, компоненты которого распределены по равномерному закону в интервале [-1; 1].
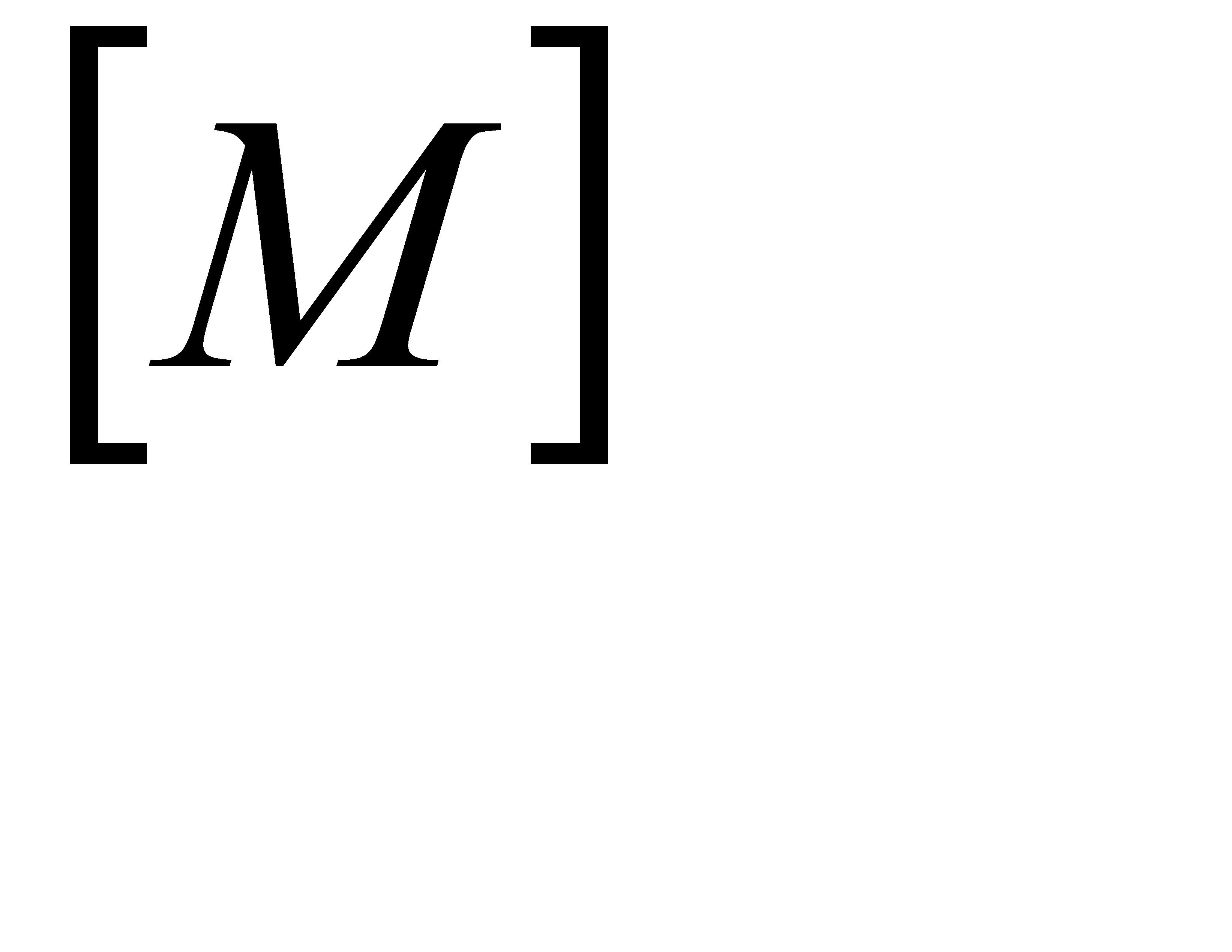 - диагональная матрица индивидуальных масштабов, размерность k×k. Заданием элементов матицы
- диагональная матрица индивидуальных масштабов, размерность k×k. Заданием элементов матицы 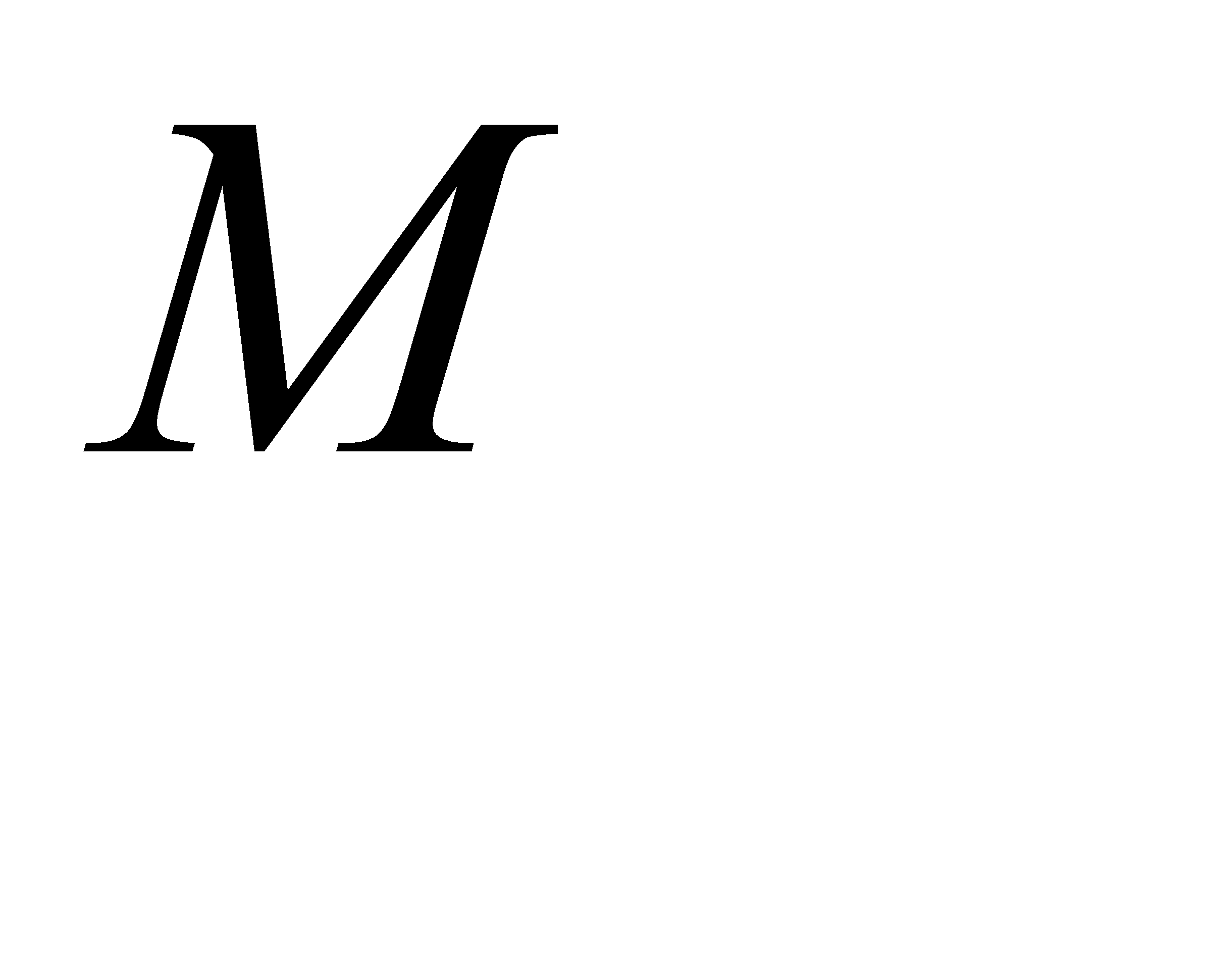 можно влиять на скорость и точность процесса поиска.
можно влиять на скорость и точность процесса поиска.
 - масштаб, задаваемый для всех k параметров вектора на i -ом шаге поиска. Эта величина зависит от числа оптимизируемых параметров, числа удачных и неудачных шагов на предыдущих этапах и др.
- масштаб, задаваемый для всех k параметров вектора на i -ом шаге поиска. Эта величина зависит от числа оптимизируемых параметров, числа удачных и неудачных шагов на предыдущих этапах и др.
При таком задании случайного шага происходит одновременный выбор направления шага и его величины. Применение методов планирования эксперимента позволяет определить чувствительность показателей качества к каждому из параметров, т.е. определить элементы матрицы 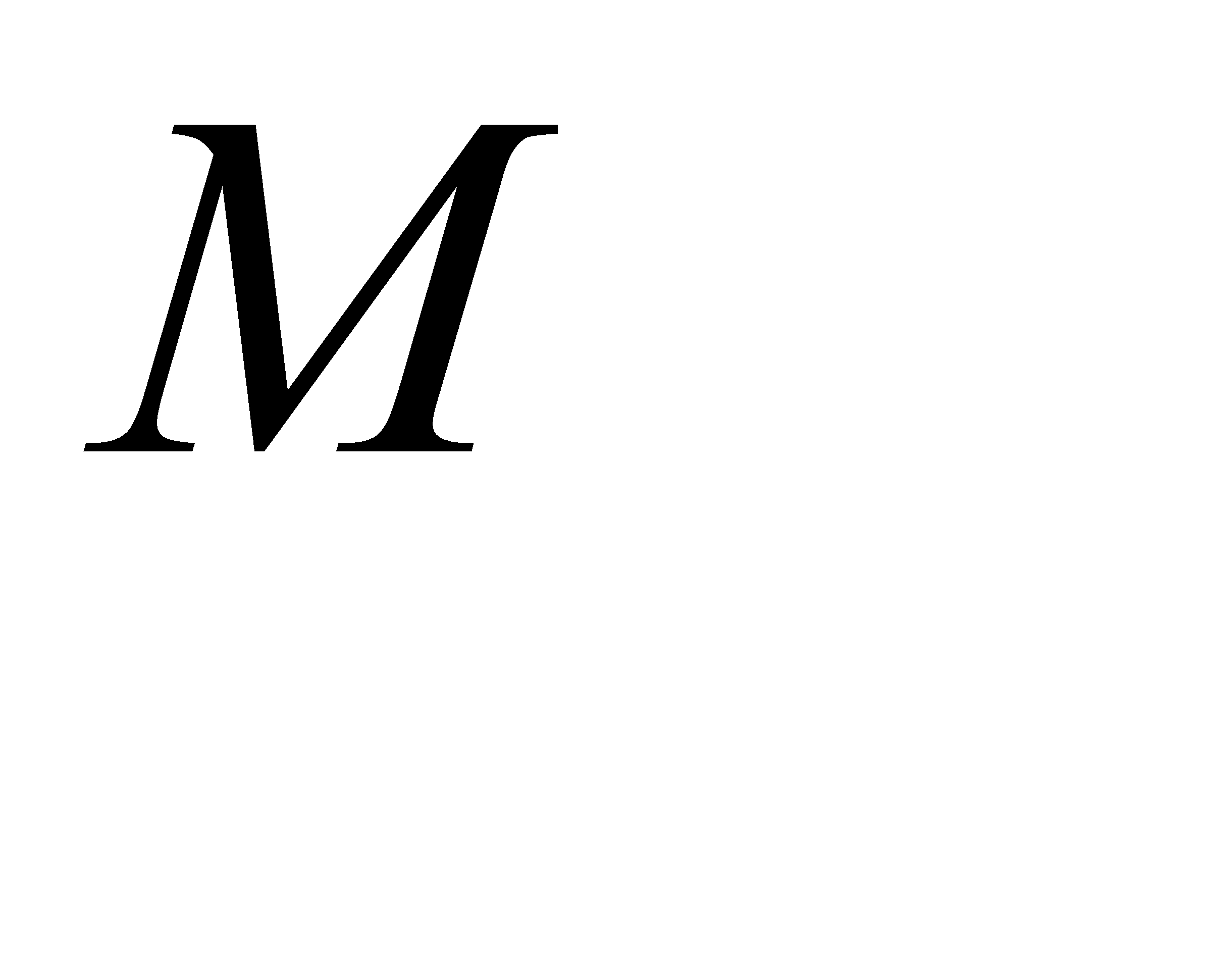 . Индивидуальные коэффициенты матрицы
. Индивидуальные коэффициенты матрицы 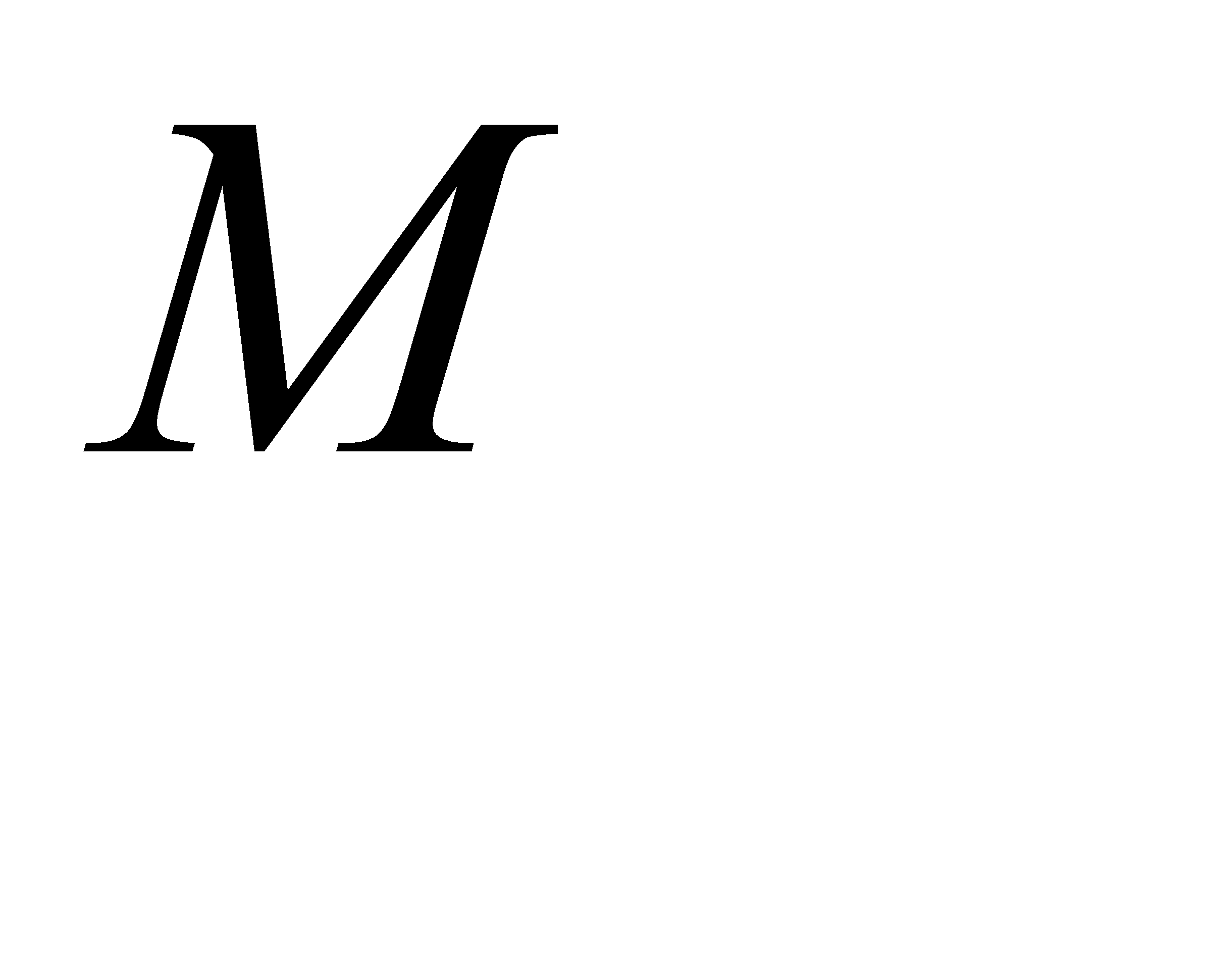 можно взять пропорциональными производным целевой функции по соответствующим переменным.
можно взять пропорциональными производным целевой функции по соответствующим переменным.
Именно на этапе оптимизации исследуемых систем проявляются существенные преимущества выбранного пути. Можно менять ограничения, исследовать любые из выбранных показателей качества, т.е. использовать возможность полиномиальных моделей в очень широких пределах без обращения к исходной сложной системе дифференциальных и алгебраических уравнений, описывающих процессы в исследуемых системах.
Из вышеизложенного следует, что применение методов планирования эксперимента позволяет существенно упростить модели системы, используемые в дальнейшем для оптимизации. Это позволяет на этапе оптимизации использовать более простые алгоритмы наряду с применением ранее указанных приёмов адаптации.
4. Разработка специального программного обеспечения решения оптимизационных задач
Системой оптимального проектирования называется совокупность методов, алгоритмов и программ, реализующих с помощью ЭВМ автоматизированный поиск на математической модели проектируемого объекта оптимальных параметров, при которых критерий оптимальности имеет экстремальное значение при условии выполнения ограничений, накладываемых требованиями стандартов, технических условий и технологий. [1].
Как уже указывалось, сложность математической модели проектируемых систем приводит к необходимости использования значительного числа различных поисковых алгоритмов, формирования комбинированных методов, применения методов, ориентированных на изменение параметров и стратегии поиска в зависимости от топологии допустимой области минимизируемой функции. Реализация указанных процедур на ЭВМ требует создания сложных программных комплексов (пакетов), представляющих проектировщику, возможность выбора нужного ему алгоритма, проведения экспериментального сравнения алгоритмов на разных классах тестовых функций, используя различные критерии эффективности и т.д.
4.1 Средства программного обеспечения
Обеспечение и автоматизация проектирования немыслим без эффективного программного обеспечения. При его разработке можно было пойти по пути использования сложившихся общих систем программирования, основывающихся на использовании универсальных алгоритмических языков. Этот путь состоит в том, что для задач оптимизации и других задач, возникающих в процессе проектирования, программируется система процедур, из которых составляется индивидуальная библиотека подпрограмм. На том же алгоритмическом языке ведётся программирование отдельных этапов проектирования с использованием индивидуальной библиотеки подпрограмм.
На таком пути организации программирования возникает ряд трудностей. Из-за высокого уровня алгоритмического языка программирование процесса проектирования может оказаться недоступным широким кругам проектировщиков. Постоянное привлечение для программирования математиков отрицательно скажется на эффективности всего процесса проектирования.
Возможен и другой путь – создание специализированных средств программного обеспечения. В настоящее время получила широкое признание такая форма организации специализированных программных средств как пакеты прикладных программ. В основе такой организации программных средств лежит модульная технология программирования.
Программный модуль – элементарная программная единица со специфическим структурой, позволяющей при помощи системных программ генерировать из модулей прикладные программы самой различной степени сложности. Комплекс модулей, ориентированных на решение определённого класса прикладных задач вместе с управляющей программой, информационной базой и соответствующей документацией образует пакет прикладных программ данного класса задач. Создание пакетов прикладных программ, ориентированна на задачи оптимального проектирования ругим программам пакет является замкнутым. С другой стороны, пакет должен обеспечивать достаточно простое расширение, т.е. включение в тело пакета новых модулей, реализующих более совершенные вычислительные алгоритмы.
4.2 Принципы организации системы поисковой оптимизации
Основными требованиями при разработке комплекса оптимизационных программ является [1]:
1. высокая модульность программ;
2. возможность расширения системы за счёт подключения новых модулей, эффективность которых проверена на тестовых и практических задачах;
3. гибкая система ввода-вывода информации, позволяющая вносить оперативные изменения в модель проектируемой системы, а также в исходные данные по результатам вычислений;
4. информация, выдаваемая в процессе должна быть понятна широкому кругу пользователей;
5.обеспечение эффективного использования алгоритмов оптимизации, включённых в систему, путём реализации процессов структурной адаптации, предусматривающих своевременную смену методов в процессе решения задачи оптимального проектирования;
6.простота управляющего языка системы при формировании заданий на проектировании с целью удобства работы инженеров –проектировщиков, не знакомых с программированием на ЭВМ.
Система по минимальным управляющим указаниям со стороны пользователя должна выполнять следующие операции:
1. формировать критерий оптимальности проектируемого объекта по его модели;
2. выбирать для каждой конкретной задачи оптимизации наиболее эффективные методы;
3. осуществлять решение задачи с их помощью в требуемой последовательности;
4. производить вывод информации о ходе решения задачи с соответствующими комментариями.
Для формирования модели объекта проектирования и выбора поисковой программы система должна использовать следующую информацию, определяющую характер и особенности решаемой задачи оптимального проектирования:
модификацию модели проектируемого объекта (указание программных модулей, реализующих модель объекта);
список ограничений;
критерий оптимальности (в случае решения задачи многокритериальной оптимизации должны быть указаны весовые коэффициенты);
требования к точности решения;
максимальное количество итераций как для отдельных поисковых алгоритмов, так и для всего процесса поиска в целом.
4.3 Структура и состав пакета программ поисковой оптимизации
Состав пакета, предназначенного для решения задач нелинейного программирования зависит от реализуемых пакетом методов и от способа общения пользователя с пакетом.
При определении способа общения пакета с пользователем обычно выбирают режим пакетной обработки. В ситуациях замены ранее заданного метода работают специальные модули, позволяющие адаптироваться к ходу решения задачи и произвести выбор более эффективного метода.
Пакет, предназначенный для работы в режиме пакетной обработки, состоит из управляющей программы и тела пакета.
Тело пакета – это набор вычислительных модулей, реализующих различные методы решения задачи НЛП.
Управляющая программа организует, в соответствии с требованиями пользователя работу вычислительных модулей, а также реализацию ряда сервисных функций.
4.4 Реализация различных стратегий выбора методов оптимизации
В [1] и ряде других работ указано на отсутствие универсального метода для решения задач НЛП, и в качестве выхода предлагается использование комбинированных алгоритмов поиска оптимального решения. Использование набора алгоритмов, реализованных на ЭВМ, в интерактивном режиме, как это предложено в [4], в процессе работы с которыми пользователь должен сам выбирать последовательность алгоритмов и их параметров, не приводит к решению проблемы, поскольку требует от пользователя высокой квалификации в области НЛП.
В проектируемых динамических системах оптимизируемая функция меняется достаточно интенсивно и весьма непредвиденным образом. Поэтому стратегия поиска и параметры алгоритмов должны изменяться в соответствии с «топологией» оптимизируемой функции. Таким образом, перспективным в теории и практике решения задач НЛП является применение и развитие принципа структурной адаптации, идея которого заключается в следующем. В некоторой локальной области оптимизируемая функция идентифицируется системой признаков, зависящих от «рельефа», числа удачных и неудачных шагов поиска и др., и характеризующих поисковую ситуацию. Для данной ситуации на основе определённых критериев из библиотеки поисковых алгоритмов выбирается наиболее эффективный, параметры которого адаптируются в процессе поиска.
| Блок исходных данных |
| Блок расчёта динамики объекта |
| Блок формирования критерия оптимальности |
| Блок распознавания ситуации |
| Печать результатов оптимизации |
| Блок оценки окончания поиска |
| Библиотека методов оптимизации |
| Блок оценки эффективности алгоритма |
Рис. 4.1 Блок-схема пакета программ оптимизации
Пакет программ оптимизации с использованием адаптивного подхода имеет модульную структуру. Блок- схема пакета программ представлена на рис. 4.1. Указанные компоненты обеспечивают выполнение следующих функций:
1. ввод основных исходных данных и печать их в виде таблицы (блок 1);
2.моделирование проектируемой системы (блок 2);
3.расчёт критерия оптимальности (блок 3);
4.идентификация поисковой ситуации и выбор из библиотеки (блок 6) соответствующего данной ситуации алгоритма оптимизации (блок 4);
5. оценка эффективности выбранного алгоритма (блок 5);
6. проверка условий окончания поиска (блок 7);
7. печать результатов оптимизации в виде таблицы (блок 8).
В пакете осуществляется идентификация следующих поисковых ситуаций  :
:
1) размерность пространства независимых переменных - 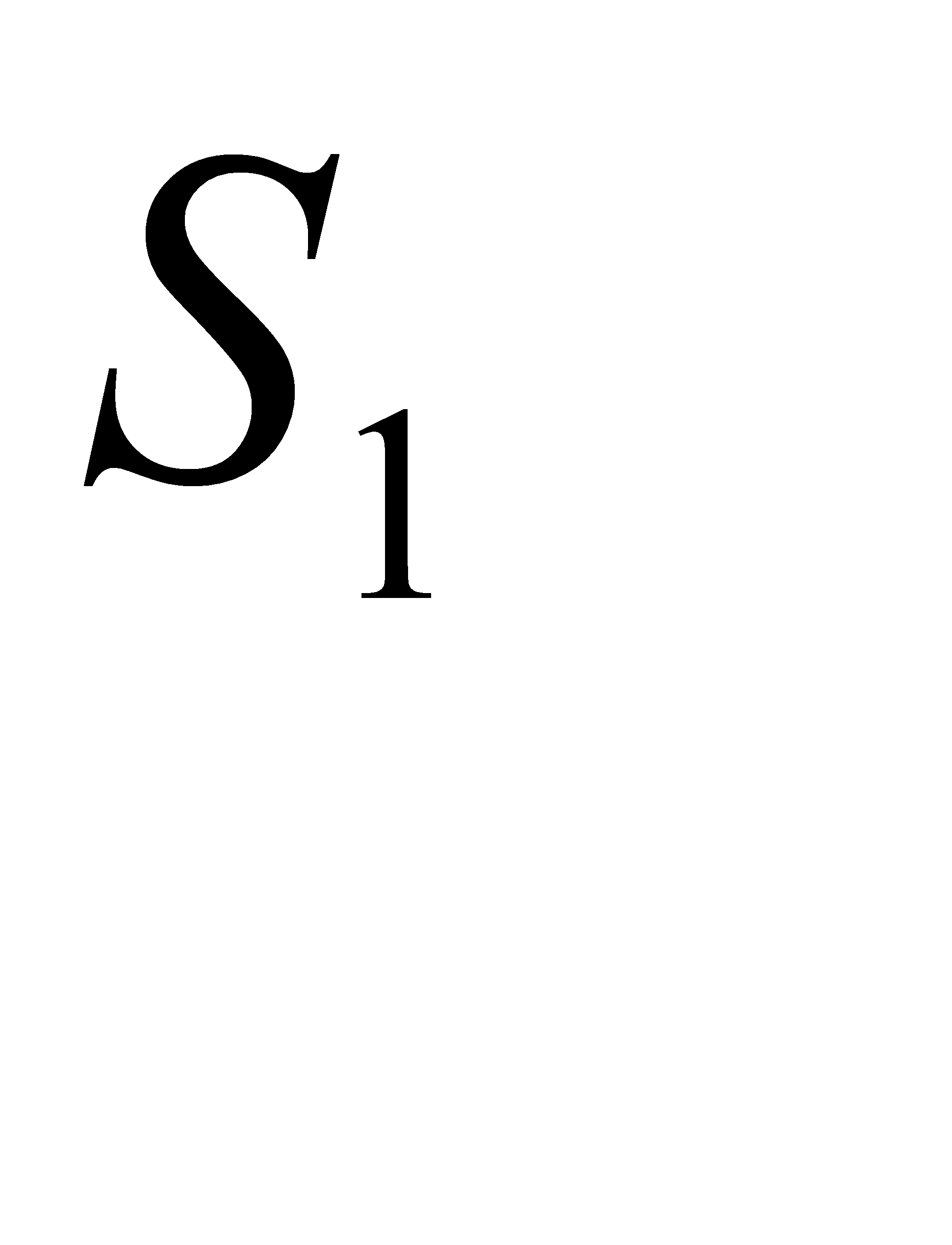 ;
;
2) крутой спуск (подъём) -  ;
;
3) площадка -  ;
;
4) окрестность экстремума -  ;
;
5) овраг - 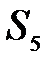 ;
;
6) многоэкстремальность -  ;
;
7) сложность объекта оптимизации, связанная с затратами машинного времени на вычисление критерия оптимизации -  .
.
Вышеуказанные ситуации достаточно полно описывают элементы «топологии» оптимизируемых функций. Сравнительный анализ различных поисковых алгоритмов даёт возможность выделить области (совокупность ситуаций) наиболее предпочтительного их использования для каждой ситуации на основе критерия  , принимающего в зависимости от некоторых условий значения 0 или 1. Допустимая область функционирования каждого из включённых в библиотеку алгоритмов определяется на основе решающих правил. Правило выбора алгоритма
, принимающего в зависимости от некоторых условий значения 0 или 1. Допустимая область функционирования каждого из включённых в библиотеку алгоритмов определяется на основе решающих правил. Правило выбора алгоритма  записывается в виде:
записывается в виде:

где  - принимает при соответствующих элементах множества
- принимает при соответствующих элементах множества  значение равное 1 и разрешает выбор алгоритма
значение равное 1 и разрешает выбор алгоритма  для данной ситуации или 0 – в противном случае.
для данной ситуации или 0 – в противном случае.
Например, решающее правило выбора алгоритма случайного поиска имеет вид
т.е. алгоритм применим в ситуациях: многоэкстремальность - 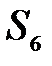 , площадка -
, площадка -  , при большой размерности пространства
, при большой размерности пространства  при
при 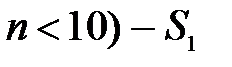 и сложном объекте оптимизации -
и сложном объекте оптимизации -  . Аналогично записываются решающие правила для других алгоритмов.
. Аналогично записываются решающие правила для других алгоритмов.
Помимо вышеуказанного, в данной работе для выбора алгоритма оптимизации используются различные подходы.
Детерминированный подход (с жёстко фиксированной последовательностью поисковых методов) заключается в следующем:
1) вдали от области экстремума используют случайные методы поиска;
2) в переходной области с помощью детерминированных методов первого порядка выходят в область экстремума;
3) в области экстремума переходят на детерминированный квадратичный или овражный метод.
Другой подход, случайный, реализует идею выбора алгоритма случайным образом с вероятностью q=1/L, где L – общее число алгоритмов в библиотеке оптимизации. Не исключается возможность выбора алгоритмов по желанию пользователя.
4.5 Описание программного обеспечения пакета
Пакет программ оптимизации содержит многочисленные программные модули, реализующие функции блоков, описанных выше. На рис. 4.2 приведена функциональная схема, иллюстрирующая взаимосвязь модулей пакета.
Основная программа обращается к модулю ввода исходных данных (M20), печати исходных данных (M721), а также к системе оптимизации (M2).
В свою очередь в M2 осуществляется обращение к подсистеме «Моделирование» (M3) для вычисления функции  , модулю идентификации поисковой ситуации поисковой ситуации и выбора метода оптимизации (M22), библиотеке методов оптимизации (M21) и модулю
, модулю идентификации поисковой ситуации поисковой ситуации и выбора метода оптимизации (M22), библиотеке методов оптимизации (M21) и модулю
| MAIN PROGRAMM |
| M20 |
| M2 |
| M721 |
| M3 |
| M22 |
| M722 |
| M222 |
| M221 |
| M21 |
| M211 |
| M212 |
| M211A |
| M212A |
| M2110 |
| M21101 |
| M2118 |
| M21181 |
| M…… |
| M…… |
| M252 |
| M251 |
| M241 |
| M28 |
| M27 |
| M26 |
| M25 |
| M24 |
| M23 |
| ......... |
| ......... |
| ......... |
| ......... |
| ......... |
| ......... |
| M251 |
Рис. 4.2 Функциональная схема связей программных модулей
пакета программ оптимизации
печати результатов оптимизации (M722). Идентификация поисковой ситуации осуществляется модулем M221, а в модуле M222 осуществляется выбор алгоритма оптимизации согласно заданию проектировщика.
Программная реализация численных методов оптимизации содержит модули двух уровней. Модуль верхнего (M211 – M2118) осуществляет дополнительные сервисные функции (печать названия метода, его параметров), а также обращение к модулю второго уровня (M211A – M21181), являющегося реализацией собственно алгоритма оптимизации.
Из каждого модуля оптимизации происходит обращение к ряду вспомогательных модулей:
M23 – модуль расчёта вектора памяти (преимущественного направления) W(I) и вероятности PW(I) функции распределения рабочего шага. Необходим для расчёта вектора направления поиска Sx(I);
M24 – модуль оценки окончания процесса поиска;
M25 – модуль принятия решения после очередного рабочего шага (определение «удачности» шага по величине приращения функции 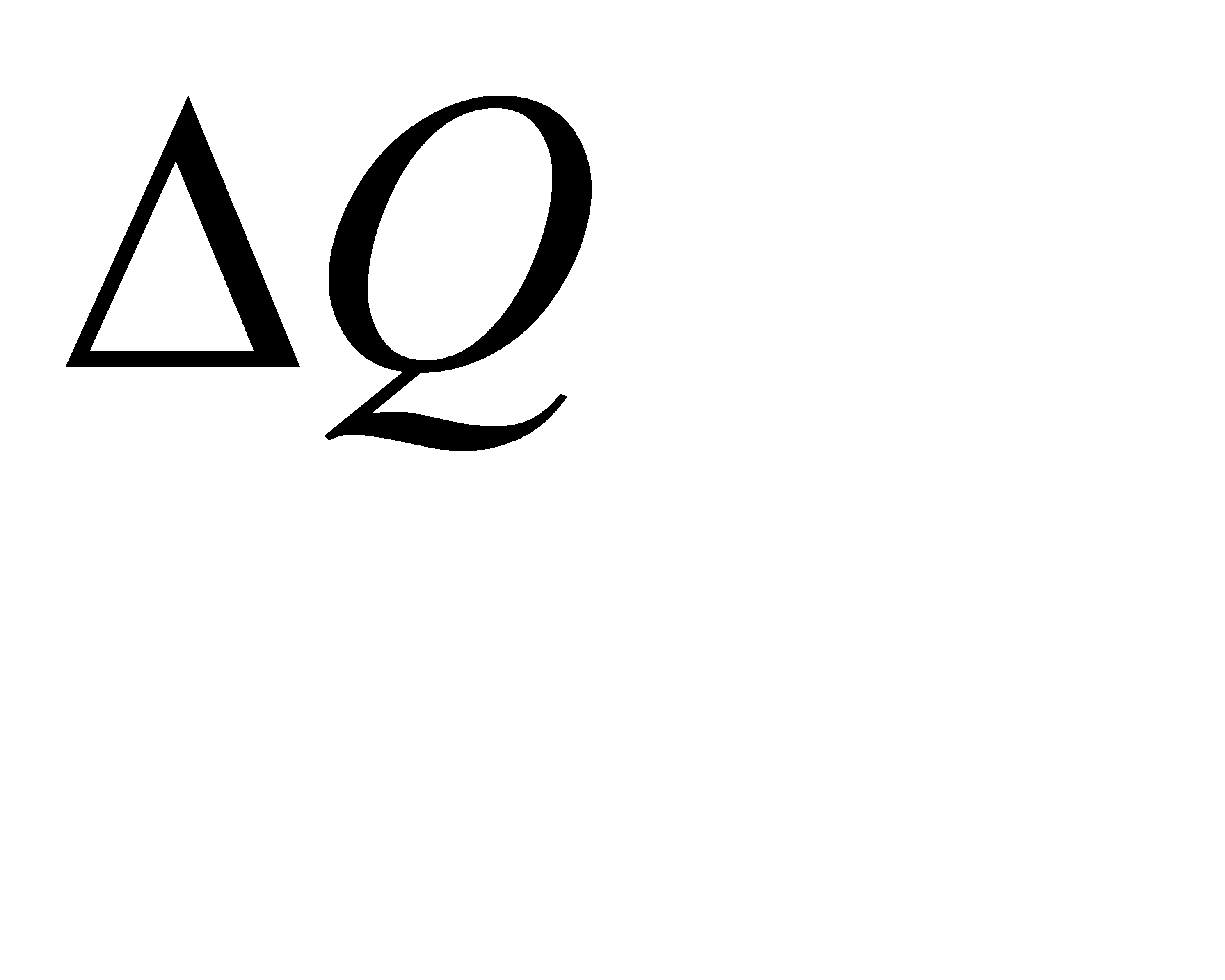 , определение общего числа «удачных» шагов, переход в новую рабочую точку при «удачном» шаге, обращение к модулю печати результатов оптимизации M722 и т.д.);
, определение общего числа «удачных» шагов, переход в новую рабочую точку при «удачном» шаге, обращение к модулю печати результатов оптимизации M722 и т.д.);
М251 – выполняют функции, аналогичные тем, которые выполняет М25, с той лишь разницей, что в М251 в зависимости от результатов
предыдущего рабочего шага вырабатывается определённый признак ситуации IER, а в М252 происходит изменение параметров алгоритма и стратегии поиска в зависимости от признака IER;
M26 – модуль расчёта величины рабочего шага XD(I) в соответствии с направлением SX(I);
М27 – модуль расчёта значений  и
и  ;
;
М28 – модуль, содержащий несколько вариантов датчика псевдослучайных чисел RAN(I), распределенных по равномерному закону в интервале от – 1 до +1;
М29 – модуль проверки ограничений  .
.
Учёт ограничений  может производится с помощью штрафных функций, имеющий вид
может производится с помощью штрафных функций, имеющий вид
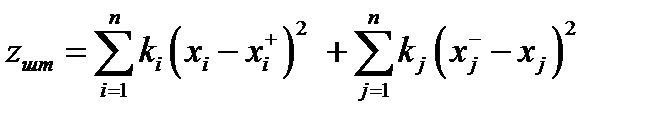 ,
,
где  ,
, 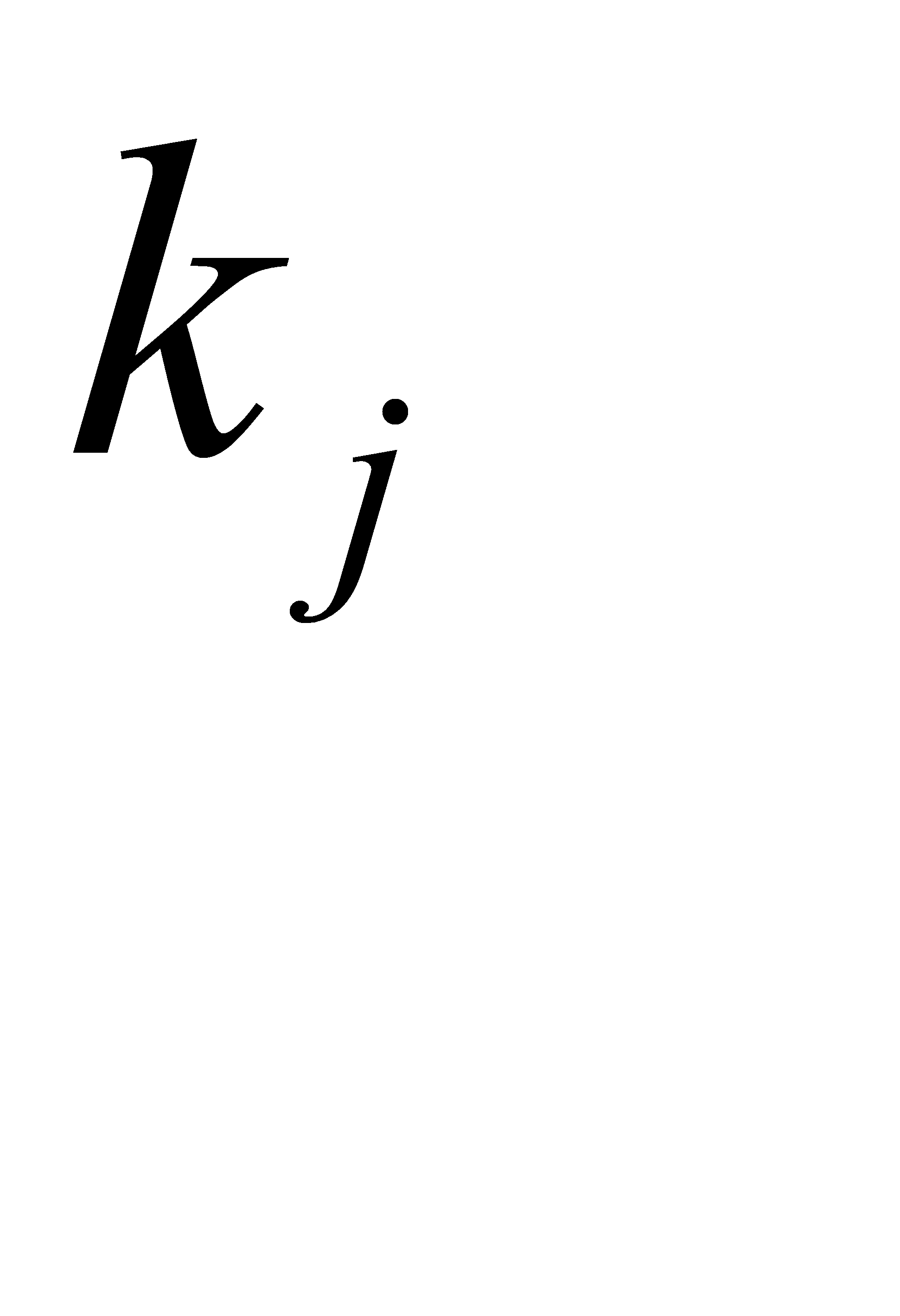 - коэффициенты штрафа,
- коэффициенты штрафа,
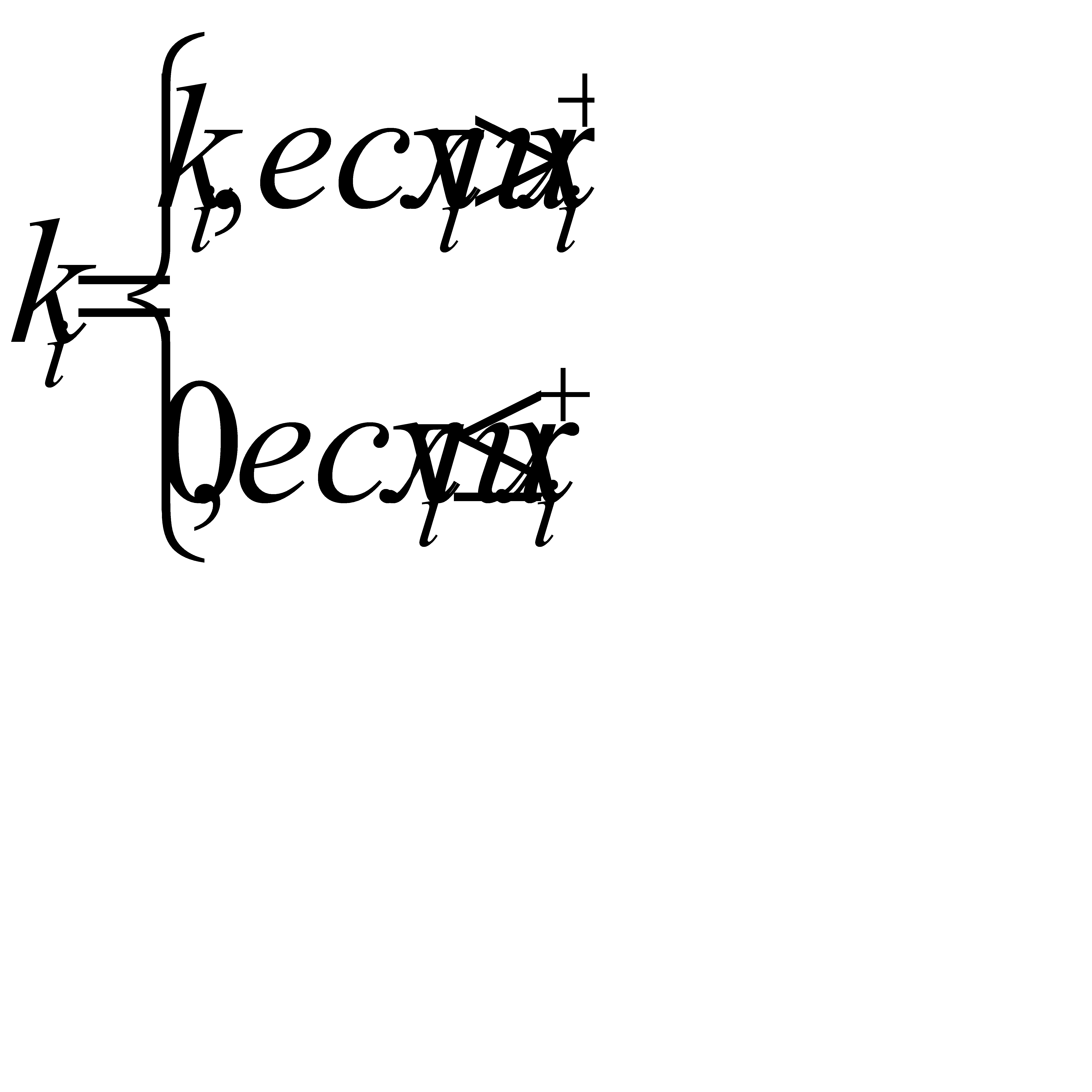 ,
, 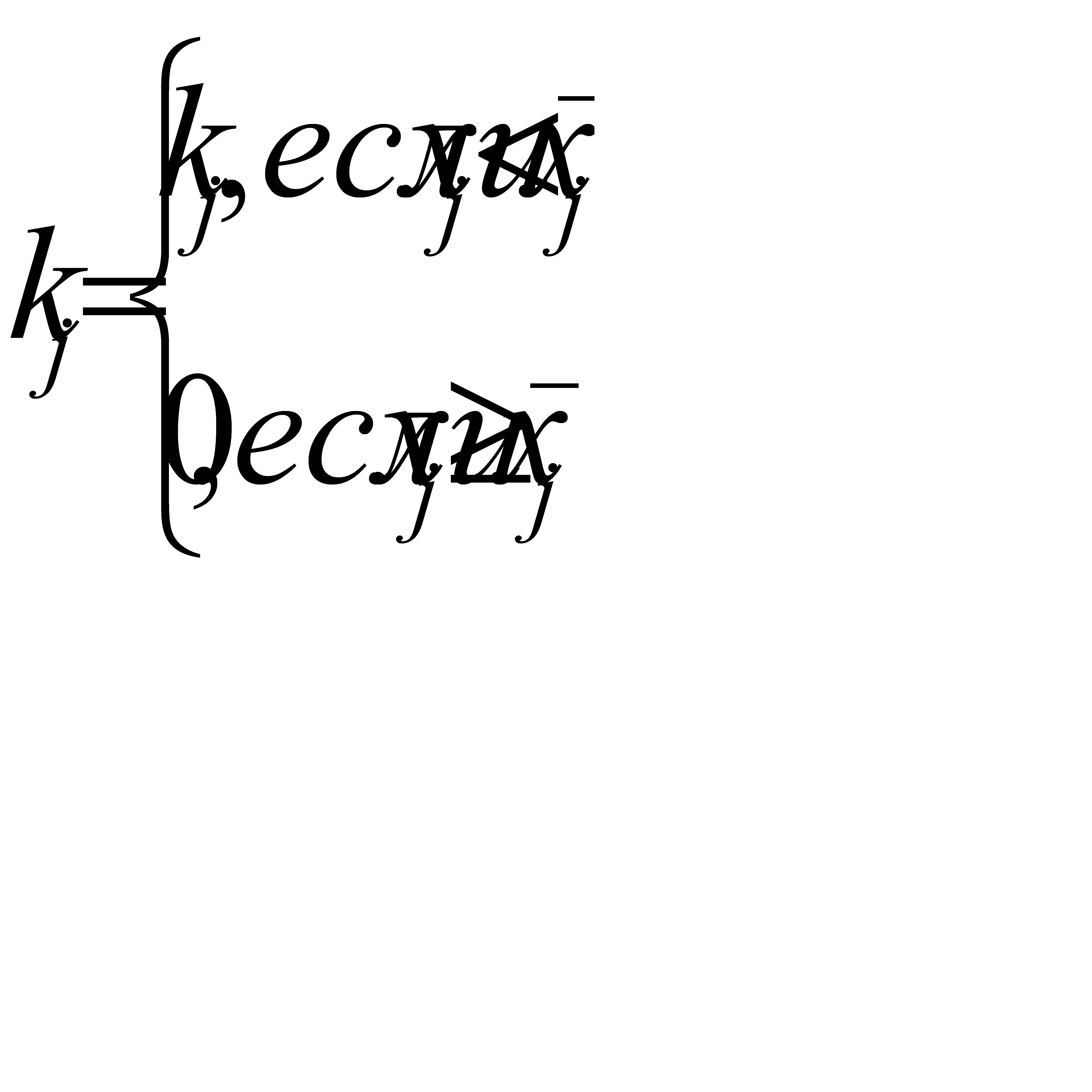
При оценке текущего значения критерия оптимальности  величина
величина 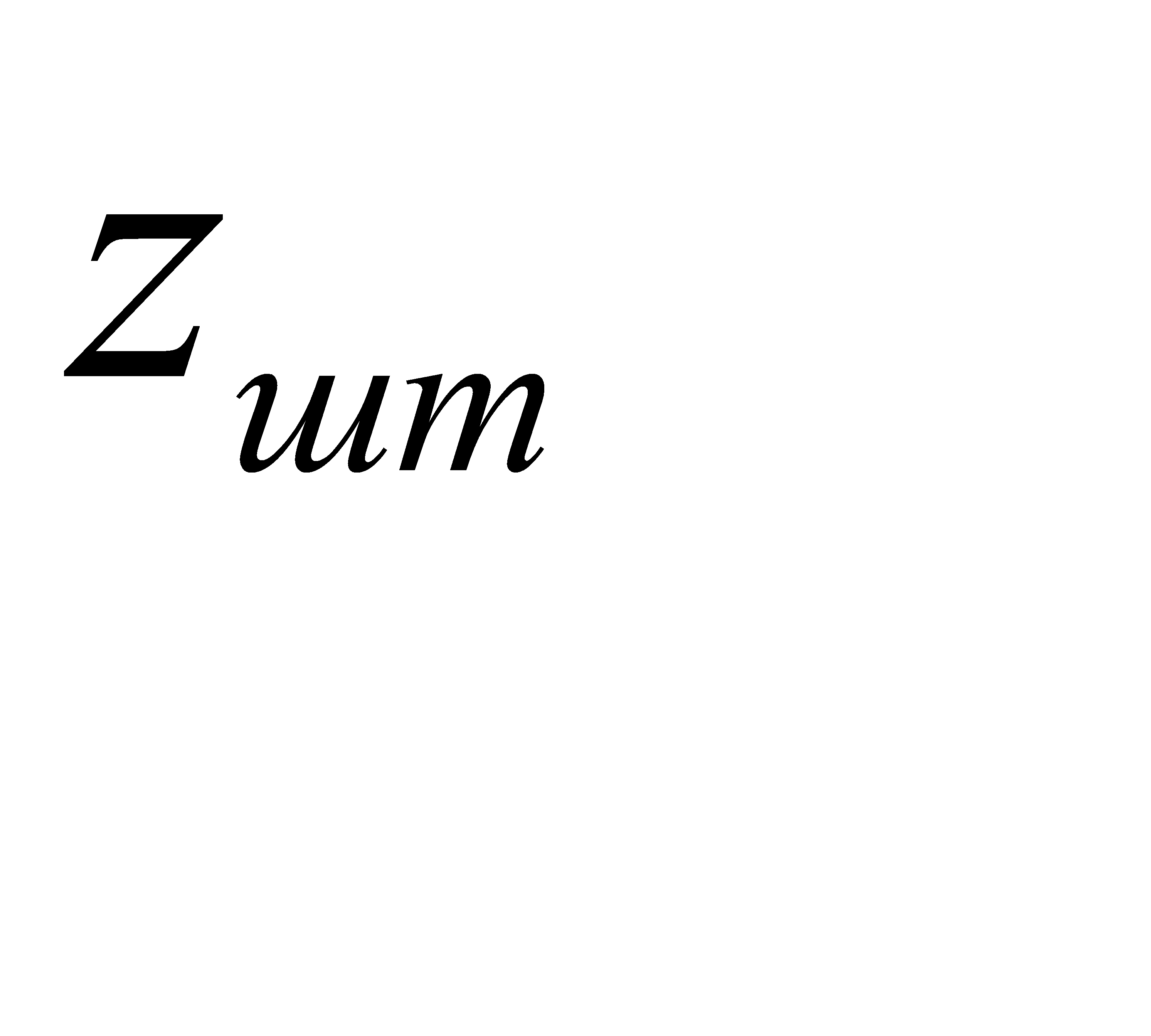 добавляется к
добавляется к  .
.
Задание параметров, необходимых для работы программ оптимизации и других программных модулей пакета, осуществляется программой BLOCK DATA. Программные модули написаны на языке ФОРТРАН – IV. Пакет функционирует в среде ОС ЕС ЭВМ с использованием базового программного обеспечения.
Для решения конкретной задачи с помощью пакета программ оптимизации необходимо:
1) выбрать методы решения задачи (при отсутствии такой информации система принимает решение об использовании того или иного метода оптимизации по одному из вариантов);
2) составить подпрограмму вычислений значений целевой функции;
3) подготовить данные о решаемой задаче – определить размерность, задать начальную точку, ограничения на независимые переменные и др.;
4) подготовить данные, управляющие ходом итерационного процесса оптимизации, а также данные для алгоритмов оптимизации;
5) осуществить проверку правильности подготовки исходных данных.
С помощью пакета программ оптимизации, возможно осуществить следующие варианты организации работы:
1) решить оптимизационную задачу с использованием одной программы, при задании начальной точки  пользователем;
пользователем;
2) использование нескольких программ оптимизации, выбираемых пользователем. Начальные точки для каждой программы задаются пользователем;
3) использование последовательности программ оптимизации, выбираемых пользователем. Начальная точка для первой программы задаётся пользователем, для последующих программ начальной точкой служит результирующая точка предыдущей программы;
4) последовательность программ оптимизации, порядок работы которых определяется не пользователем, а блоком выбора метода оптимизации в соответствии с поисковой ситуацией. Начальная точка поиска задаётся пользователем.
Входными данными о решаемой задаче оптимизации являются (для массивов в скобках указаны максимальные их размерности):
Не нашли, что искали? Воспользуйтесь поиском: