Выбор независимых переменных 12 страница

позволяет вычислять последние с использованием коэффициентов передаточной функции замкнутой скорректированной системы. При этом не требуется интегрирования системы дифференциальных уравнений САУ, а решение задачи НЛП сводится к поиску параметров корректирующего устройства из условия минимума критерии I₂, значение которого на каждом шаге оптимизации вычисляется по формулам приложения 32 [91].

6.2 Параметрический синтез САУ средствами LabVIEW

LabVIEW- это программная среда, использующая язык графического программирования G. Этот язык был создан специально для инженеров и ученых. Идея, стоящая у истоков создания LabVIEW была в том, чтобы формализовать этап формирования блок-схем используемых систем и убрать текстовые инструкции. С использованием языка G программа представляется не в виде схематического текстового описания,а в виде графического представления основных операторов программирования и проводников потока данных,определяющих последовательность выполнения программы на блок-диаграмме [120].

В LabVIEW интерфейс пользователя создается с использованием множества элементов. По аналогии с реальным прибором интерфейс пользователя называется лицевой панелью. Исходная программа на языке G называется блок-диаграммой,для создания которой программист использует множество функций. Программа,написанная в среде LabVIEW, называется виртуальным прибором. Таким образом, интерактивные графические лицевые панели виртуального прибора обеспечивают управление программой и представление данных.

При решении поставленной задачи параметрического синтеза корректирующего устройства САУ были разработаны два виртуальных прибора ВП1 и ВП2 [120].

ВП1 позволяет:

1. Задавать любые передаточные функции вида

2. Задавать структуры корректирующих устройств в соответствии с заданием.

3. Рассчитывать и отображать:

- переходную функцию h(t);

- частотные характеристики ЛАЧХ и ЛФЧХ;

- корни числителя и знаменателя передаточной функции;

- передаточную функцию исходной и скорректированной САУ.

4. Оценивать качество переходного процесса по величинам максимального значения переходной функции, перерегулированию и времени регулирования;

5. Проводить анализ устойчивости системы и делать вывод о характере переходного процесса.

ВП2 включает все свойства ВП1 и позволяет:

1. Осуществлять процесс оптимизации как для каждого параметра корректирующего устройства, так и для их совокупности;

2. Рассчитывать и отображать текущие и удачные:

- переходные функции системы;

- параметры корректирующего устройства;

- значения показателей качества переходного процесса.

Для решения задачи оптимизации переходного процесса критерии оптимальности формируются в следующем виде:

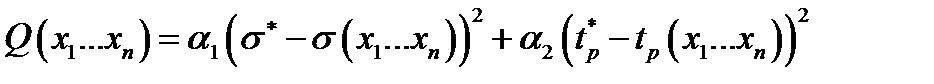
где - весовые коэффициенты;

- требуемые показатели динамики САУ;

- текущие значения тех же показателей, получаемых в результате вариации параметров корректирующего устройства.

Численное интегрирование дифференциальных уравнений системы осуществляется с использованием 4-х точечного метода Рунге — Кутты. Имеется возможность применения также методов Эйлера и Адамса.

При выборе шага интегрирования руководствуются следующим правилом: величина шага интегрирования не менее чем в 10 раз меньше минимальной постоянной времени звена, входящего в передаточную функцию всей системы. Для оптимизации параметров корректирующего устройства запускают ВП2. При этом перед началом счета необходимо задать большую величину функции качества переходного процесса, так как исходная система неустойчива и корни знаменателя передаточной функции лежат в правой полуплоскости (о чем свидетельствует картина расположения корней на комплексной плоскости).

В качестве метода оптимизации используется случайный поиск с переменной величиной шага. Критерием окончания процесса оптимизации является исчерпание ресурса числа итераций. Оптимизация осуществляется как для отдельного параметра, так и для совокупности параметров корректирующего устройства САУ.

Процесс оптимизации и его завершение можно наблюдать на лицевой панели ВП2 с помощью окна, в котором отражаются картины переходных процессов для текущих и удачных значений оптимизируемых параметров корректирующего устройства.

6.3. Параметрический синтез САУ средства MATLAB

Для выполнения сложных математических расчетов применяют компьютеры, в которых исполняютя программы, написанные пользователями на языках Fortran, Pascal и Basic и др. Программирование является достаточно трудоемкой операцией и занимает большую часть времени, отведенное для решения задачи. В настоящее время для выполнения расчетов на компьютере, с успехом можно использовать готовые процедуры и функции, которые имеются в системах автоматизации математических расчетов. Одной из таких проверенных временем и тщательно проработанных систем является MATLAB, разработанная корпорацией Math Works и поставляемая как комплекс MA + Simulink.

Система MATLAB состоит из пяти основных частей[121]:

1) среда разработки- набор инструментов и средств, которые помогают использовать функции и файлы MATLAB. Большая часть этих инструментов является графическими.

2) Библиотека математических функций MATLAB- обширный комплекс вычислительных алгоритмов от элементарных до сложных функций, осуществляющих решение систем уравнений, численное интегрирование, оптимизацию и др.

3) Язык программирования MATLAB включает в себя свойства языка объектно-ориентированного программирования с управляющей логикой, функциями, структурой данных, вводом и выводом данных.

4) Графика содержит средства для двух или трехмерной визуализации, функции для обработки изображений, анимации и составления графиков для презентации.

5) Программный интерфейс приложения MATLAB-библиотека, которая позволяет взаимодействовать системе MATLAB с программами, написанными на языках Cи, Fortran и др.

Simulink является пакетом программ, расширяющим функциональность MATLAB. При помощи Simulink можно создавать, моделировать и анализировать такие динамические системы как механические, электрические, термодинамические и др. Моделирование в Simulink происходит в две стадии. Во-первых формируется графическая модель системы в виде блок-схемы с использованием редактора моделей Simulink и в которой отражается зависимость входов и выходов системы от времени

На втором этапе, после создания модели выбирается метод численного интегрирования, шаг и время интегрирования. Результаты моделирования отображаются с использованием блока Scope и других блоков. Для получения непрерывного решения дифференциальных уравнений с фиксированным шагом используют следующие численные методы интегрирования: метод Эйлера, улучшенный метод Эйлера, метод Рунге-Кутты 4-ого порядка.

В работе [121] подробно описана процедура формирования модели нескорректированной следящей САУ. Для исследования САУ на устойчивость используется критерий Найквиста. Возможно использование в среде MATLAB и логарифмических амплитудных и фазовых частотных характеристик.

Оптимизация параметров корректирующего устройства происходит при помощи инструментального пакета NCD-Blockset, которые предоставляет в распоряжение пользователя графический интерфейс для настройки параметров динамических объектов, обеспечивающих желаемое качество переходных процессов. Задание ограничений на динамику системы осуществляется в визуальном режиме путем задания коридора, в пределах которого должен находиться выходной сигнал САУ. На базе этих ограничений NCD-Blockset автоматически генерирует задачу конечномерной оптимизации [121]. Эта задача решается с привлечением процедуры квадратичного программирования из пакета Optimization Toolbox [124]. Ход оптимизации контролируется на экране с помощью отображения графика контролируемого процесса и текущих значений минимизируемой функции. По окончанию процесса оптимизации, оптимальные значения настраиваемых параметров корректирующего устройства сохраняются в рабочем пространстве MATLAB.

Optimization Toolbox включает программы широко известных методов минимизации линейных и нелинейных функций. Эти программы могут быть использованы для решения сложных задач в различных областях науки и техники. В пакет включены версии традиционных и новейших алгоритмов оптимизации, в том числе безусловная оптимизация, условная, многокритериальная, методы линейного и квадратичного программирования. Ведущий раздела- Трифонов А.Г. - доктор технических наук, главный научный сотрудник лаборатории моделирования Объединенного института энергетических и ядерных исследований Национальной Академии наук Беларуси. Материалы раздела Optimization Toolbox, книги по методам оптимизации, в том числе и работа Трифонова А.Г. ''Постановка задачи оптимизации и численные методы ее решения'' приведены в Интернете на сайте MATLAB. Exponenta.ru.

6.4 Параметрический синтез САУ средствами МВТУ 3.5

Программный комплекс '' М оделирование В Т ехнических У стройствах'' (МВТУ), разработанный сотрудниками Московского государственного технического университета им. Н.Э. Баумана [117,118] позволяет проводить моделирование, частотный анализ и оптимизацию САУ, аналогично тому, как это осуществляется с помощью инструментальных систем LabVIEW [106-110] и MATLAB [111-116].

Рассмотрим процесс проектирования САУ на примере нахождения оптимальных параметров корректирующего устройства следящей системы [119] средствами программного комплекса МВТУ. Подробное описание этого процесса дано в [122, 123].

На первом этапе с помощью элементов МВТУ и линий связи формируется структурная схема исследуемой нескорректированной САУ. После ввода параметров звеньев(коэффициентов усиления и постоянных времени) осуществляется формирование параметров, необходимых для моделирования: шаг интегрирования, минимальный шаг интегрирования, численный метод интегрирования (например, метод Эйлера) и др. При выполнение следующего этапа происходит открытие графического окна и изменение его свойств (масштабы по осям X и Y, минимальные и максимальные значения выходной координаты и др.). После редактирования графического окна производим расчет переходного процесса нескорректированной САУ, убеждаемся, что система неустойчива и нуждается в коррекции. Отметим, что для моделирования системы, помимо метода Эйлера, могут быть использованы 4-х точечный метод Рунге-Кутты, неявные метод Эйлера, метод Адамса и др. [2, 117,118].

Средствами МВТУ может быть проведен анализ амплитудно-фазовых частотных характеристик нескорректированной системы. После назначения параметров частотного анализа (значение начальной и конечной частот, количество точек вывода и др.) получаем, в зависимости от задания, либо логарифмические частотные характеристики, либо годограф Найквиста, либо кривую Михайлова. На этапе оптимизации параметров корректирующего устройства вводим в блок-схему исходной САУ корректирующее звено и присваиваем его параметрам начальные значения полученные в результате ''ручного'' счета с использованием ЛАЧХ [125]. Далее формируя локальные критерии оптимизации (перерегулирование и время регулирования ) в соответствии с [122], получаем структурную схему скорректированной системы с соответствующими ''измерителями''. После чего с помощью диалоговых окон задаем численные занчения параметров и критериев оптимизации. Диалоговое окно ''Параметрическая оптимизация'' служит также для задания метода поиска, вида критерия оптимальности, числа итераций. После назначения метода численного интегрирования и его параметров запускается процесс оптимизации[122,123]. При нажатии клавиши ''Результаты оптимизации'' получаем искомые параметры корректирующего устройства и график переходного процесса в скорректированной системе.

После этого пользователь принимает решение либо об окончании процесса поиска, либо о продолжении расчетов с измененной структурой корректирующего устройства, другими исходными параметрами, другим численным методом оптимизации и др.

Вышеописанный программный комплекс МВТУ [117,118] позволяет оперативно решать подобного рода задачи, встречающиеся как в учебном процессе, так и в научных исследованиях.

Заключение

В данной работе автор, руководствуясь собственным опытом решения задач оптимизации, постарался достичь следующих целей, для чего, собственно и предполагался выпуск данного конспекта лекций по дисциплине ''Автоматизация проектирования систем и средств управления'':

– ознакомление с постановкой задач оптимизации и методами их решения;

– получение практических навыков решения оптимизационных задач на компьютере, как с использованием программ собственной разработки, так и с использованием программных комплексов, разработанных крупными корпорациями;

– формирование представлений о сравнительной эффективности рассмотренных методов оптимизации и границах их применения.

Насколько автору это удалось, судить Вам, дорогой читатель.

Автор будет благодарен замечаниям и дополнениям, высказанными читателями данного конспекта лекций.

ЛИТЕРАТУРА

1. Моисеев Н. Н., Иванилов Ю. П, Столярова Е. М. Методы оптимизации. М.: Наука, 1978. – 348 с.

2. Сольницев Р. И. Автоматизация проектирования систем управления М.: Высшая школа, 1991.-335 с.

3. Уайлд Д. Дж. Методы поиска экстремума. М.: Наука, 1967.-267с.

4. Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975. – 534 с.

5. Батищев Д. И. Поисковые методы оптимального проектирования. М.: Совесткое радио, 1975. – 216 с.

6. Алгоритмы оптимизации проектных решений./ Под ред.Половинкина А. И./ М.: Энергия, 1976, -265 с.

7. Геминтерн В. И., Каган Б. М. Методы оптимального проектирования. М.: Энергия, 1980. – 160 с.

8. Минимизация в инженерных расчётах на ЭВМ. Библиотека программ. /

С. Ю. Гуснин и др. М.: Машиностроение. 1981. -120 с.

9. Страхов С. В. и др. Динамика АСЭ с пневномеханическим приводом постоянной скорости.- Электричество, 1970, №11, с. 31-35.

10. Страхов С. В., Трубачёв В. Т. Динамика автономной системы с гидромеханическим приводом постоянной скорости.- Электричество, 1972 №1, с. 34-37.

11. Дехтяренко В. А., Своятыцкий Д. А. Методы многокритериальной оптимизации при проектировании. Препринт ИК АН УССР, Киев.- 1976.

12. Монахов О. И. Выбор весовых коэффициентов в задаче поиска параметров эквивалента. Труды МИИТа, 1975, вып. 498, с. 23-29.

13. Страхов С. В. и др. Исследование возможностей применения методов нелинейного программирования для синтеза оптимальных регуляторов в автономных энергосистемах- «Известия ВУЗов. Электромеханика», 1980, №12, с. 1296-1302.

14. Лазарев И. Б., Валуйских В. П. Экспериментальное сравнение алгоритмов случайного поиска.- «Автоматика и вычислительная техника», 1974, №2,. с. 57-60.

15. Растригин Л. А., Рипа К. К. Сопоставление методов наискорейшего спуска и случайного поиска с обучением — В сб.: «Проблемы случайного поиска», Рига, «Знание», 1986, с. 87-92.

16. Захаров В. В., Филипенко Н. М. Сравнение случайного поиска со схемой скорейшего спуска на тестовых функциях.- «Автоматика и вычислительная техника», 1972, №1.

17. Зак Ю. А., Кондращин Г. П., Ленин А. П. Исследование алгоритмов случайного поиска в задачах оптимизации сложных систем.-В сб.: «Проблемы случайного поиска», Рига, «Знание», 1973, вып. 2, с. 131-150.

18. Гурин Л. С. К вопросу о сравнительной оценке различных методов оптимизации.- «Автоматика и вычислительная техника», 1965, №10.

19. Чалый Г. В., Билинкис П. Г., Непомнящий М. А. Выбор эффективного метода оптимизации электрических машин с помощью ЭВМ.- В кн.: «Электроэнергетика и автоматика», Кишинёв, 1974, вып.20.

20. Антамошкин А. Н. О быстродействии алгоритмов случайного поиска. – «Автоматика и вычислительная техника», 1975, №3, с. 38-44.

21. Талалай А. М. К сравнению различных реализаций методов градиента и статистического градиента.- «Автоматика и вычислительная техника», 1975, №6.

22. Терзян А. А. Сопоставительный анализ методов поисковой оптимизации в классе задач синтеза электрических машин.- В кн.: «Проблемы случайного поиска», вып. 7. Рига.: Знание, 1978, с. 214-237.

23. Аветисян Д. А., Соколов В. С., Хан В. х. Оптимальное проектирование электрических машин на ЭВМ. М.: Энергия, 1976. – 208 с.

24. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной оптимизации. – М.: Мир, 1972. – 240 с.

25. Растригин Л. А. Системы экстремального управления. М.: Наука, 1974. – 630 с.

26. Растригин Л. А. Статистические методы поиска.- М.: Наука, 1968.- 376 с.

27. Растригин Л. А. Случайный поиск с линейной тактикой.- Рига.: Знание,1971.- 192 с.

28. Растригин Л. А. Методы статистической оптимизации.-Рига.: Знание, 1968.

29. Растригин Л. А. Случайный поиск в процессах адаптации.-Рига.: Знание, 1973.- 132 с.

30. Теория и применение случайного поиска. Под ред. Растригина Л. А.-Рига.: Знание, 1969.- 309 с.

31. Алгоритмы и программы случайного поиска. Под ред. Растригина Л. А.-Рига.: Знание, 1969.- 374 с.

32. Применение методов случайного поиска в САПР. Таллин.: Валгус, 1980, ч. 2.

33. Каган Б. М., Даниленко С. Е. Применение метода случайного поиска с обучением при оптимальном проектировании асинхронных двигателей.- В кн.:«Автоматика и вычислительная техника», Рига.: Знание,1966, вып. 13, с 169-172.

34. Растригин Л. А., Тарасенко Г. С. Об одном алгоритме случайного поиска.- В сб.: Проблемы случайного поиска, вып. 3, Знание,1974, с. 108-112.

35. Трахтенберг В. С. Алгоритм и программа многомерной экстраполяции.- В кн.: Алгоритмы и программы случайного поиска.-Рига.: Знание,1969, с. 223-241.

36. Фурунжиев Р. Г. Автоматизированное проектирование колебательных систем. – Минск.: Высшая школа, 1977. – 451с.

37. Вишневский Б. Л., Григорян В. Г. Применение алгоритмов поиска для аппроксимации экспоненциальных временных характеристик динамических систем.- В сб.: «Вопросы теории автоматического управления», Изд. ЛГУ, вып. 3, 1977, с. 61-66.

38. Захаров В. В., Крутиков В. Н. Повышение эффективности алгоритмов случайного поиска посредством их включения в систему экстраполяции. В сб.: «Проблемы случайного поиска», вып. 7, Рига.: Знание,1978, с. 207-213.

39. Севриткин К. П. Стандартная программа оптимизации многопараметрических систем методом случайного поиска.- В кн.: Алгоритмы и программы случайного поиска.- Рига.: Знание, 1968, с. 85-95.

40. Ларин А. Г. и др. Машинная оптимизация электронных узлов РЭА.- М.: Сов. Радио, 1978.- 192 с.

41. Пашкеев С. Д., Минязов Р. И., Могилевский В. Д. Машинные методы оптимизации в технике связи. Учебное пособие для ВУЗов, - М.: Связь, 1976.- 272 с.

42. Шуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 238 с.

43. Гельфанд И. М., Цетлин М. Л. Принцип нелокального поиска в системах автоматической оптимизации. ДАН СССР, т. 197, 1961, №2, с. 295-298.

44. Волынский Э. И., Филатов Г. В. К вопросу об адаптации шага в алгоритмах случайного поиска.- Автоматика и вычислительная техника, 1974, №4, с. 66-71.

45. Павлов В. Ю., Солдатов В. Е. О решении одного класса судостроительных задач оптимизации. Труды Ленинградского кораблестроительного института, вып. 97, с. 110-113.

46. Теория автоматического управления. Ч. 2. Под ред. Воронова А. А. М.: Высшая школа, 1977.- 228с.

47. Короп В. Ф. Локально-глобальный поиск коллективом автоматов Буша-Мостселлера.- «Автоматика и вычислительная техника», 1975, №2, с. 26-29.

48. Черноусько Ф. Л. Об оптимальном поиске экстремума унимодальных функций. – Журнал вычисл. мат. и мат. физ., 1970, т. 10, № 4, с. 922-934.

49. Черноусько Ф. Л. Об оптимальном поиске минимума выпуклых функций. – Журнал вычисл. мат. и мат. физ., 1970, т. 10, № 6, с. 1355-1366.

50. Захаров В. В. Тестовые задачи оптимизации. В кн.: Тезисы докладов Всесоюзного научно-технического семинара. «Численные методы нелинейного программирования». Харьков, 1979 ч. II.

51. Норенков И. П., Маничев В. Б. Системы автоматизированного проектирования электронной и вычислительной аппаратуры. М.: Высшая школа. 1983. – 272 с.

52. Чурилов А. И., Кулик Е. Г. Применение алгоритмов случайного поиска для решения нелинейных уравнений, описывающих электронные схемы. - Автоматика и вычислительная техника, 1975, №3, с. 52-57.

53. Шкварцов В. В., Орленко Н. Н. Опыт экспериментального сравнения алгоритмов случайного поиск. В кн.: Проблемы статистической оптимизации. Рига, 1968, с. 93-98.

54. Оганесян Э. В., Степанян Э. А. О сравнительной оценке различных алгоритмов случайного поиска. В кн.: Методы статистической оптимизации. Рига. 1968. с. 111-122.

55. Терзян А. А. Автоматизированное проектирование электрических машин. – М.: Энергоатомиздат, 1983. -255 с.

56. Растригин Л. А., Рипа К. К., Тарасенко Г. С. Адаптация случайного поиска. Рига: Знание, 1978. – 242 с.

57. Сухарев А. Г. Оптимальный поиск экстремума.- М.: Московский гос. университет,1975.-100с.

58. Полак Э. Численные методы оптимизации. Единый подход. М.: Мир. 1974. – 363 с.

59. Гилл Ф. и Мюррей У. Численные методы условной оптимизации – М.: Мир., 1977 – 296 с.

60. Паппас Н., Моранди Р. Усовершенствованный алгоритм прямого поиска для задач математического программирования. Труды Американского общества инженеров-механиков. Конструирование и технология машиностроения, 1975, №4, с. 208-213.

61. Возич М., Хейдт Г. Гиперконический случайный поиск. Труды Американского общества инженеров-механиков. Динамические системы и управление, 1972, №1. с. 87-96.

62. Математическое обеспечение ЕС ЭВМ. Институт математики АН БССР. Минск, 1978, вып. 17-114 с.

63. Математическое обеспечение ЕС ЭВМ, Институт математики АН БССР. Минск, 198ё, вып. 34.

64. Адаменко Г. М. Алгебраическая модель алгоритмов минимизации. – ДАН БССР, XXII, № 9, 1978, с.801-803.

65. Адаменко Г. М. Алгебра алгоритмов минимизации и структурная адаптация. В кн.: Структурная адаптация многомашинных систем обработки информации. Рига.: Знание, 1978, с. 69-73.

66. Адаменко Г. М. Решение экстремальных задач в условиях неполной информированности. – Автоматика и вычислительная техника, 1980, №4, с. 53-59.

67. Современное состояние теории исследования операций /Под ред. Н. Н. Моисеева. М.: Наука, 1979. -464 с.

68. Кузина Г. Ф., Чуян Р. К. АСОПР – автоматическая система оптимального проектирования. В кн.: Тезисы докладов III Всесоюзной конференции по исследованию операций. – Горький, 1978, - 300 с.

69. Батищев Д. И., Бедная Р. И. Особенности организации пакетов программ оптимизации, используемых в САПР. – В кн.: Автоматизированное проектирование в радиоэлектронике и приборостроении. – Л.: Известия ЛЭТИ, 1977, вып. 224, с. 12-29.

70. Состав и функциональные характеристики пакета программ математического программирования / Богданов А. В., Демин Б. С. и др. – Управляющие системы и машины, 1976, №2, с. 40-42.

71. Брябрин В. М., Евтушенко Ю. Г., Семовский С. В. Диалоговая система оптимизации. – В кн.: Численные методы нелинейного программирования. Тезисы II Всесоюзного семинара. Харьков, 1976, с. 3-7.

72. Амелина Н. И., Жак С. В., Пестрикова Е. Я. Пакет оптимизационных программ со структурной адаптацией. – В кн.: Численные методы нелинейного программирования. Тезисы Всесоюзного семинара. Харьков, 1979, ч. II, с. 39-42.

73. Петренко А. И., Тимченко А. П., Ладогубец В. В., Мачуговский В. С. Общая характеристика блока параметрической оптимизации пакета прикладных программ СПАРС. – Управляющие системы и машины., 1983, №1, с. 33-38.

74. Коротаева Л.Н., Панишев А.В. Программа нахождения глобального экстремума функции многих переменных. В кн.: Алгоритмы и программы случайного поиска. Рига. «Знание» 1968, с. 179-189.

75. Растригин Л.А., Рипа К.К. Непрерывный алгоритм самообучения при многопараметрической оптимизации методом случайного поиска.- «Автоматика и вычислительная техника». Рига, 1965, №10, с. 55-76.

76. Калинников Ю.С., Лившиц А.Л. О некоторых модификациях алгоритма глобального статистического поиска по направляющей сфере.- В кн.: «Задачи статистической оптимизации». Рига. «Знание», 1971, с. 197-202.

77. Валуйских В.П. Об одном алгоритме случайного поиска для оптимизации систем при наличии ограничений. «Автоматика и вычислительная техника», 1973, №6, с. 43-45.

78. Гуляев В.В., Суханов Ю.Н. Алгоритм поиска глобального экстремума с распознаванием структуры оптимизируемой функции.- «Автоматика и вычислительная техника», 1971, №1, с. 46-51.

79. Растригин Л.А. Смешанные алгоритмы случайного поиска.- В кн.: «Проблемы случайного поиска», Рига. «Знание», 1973, вып.3.

80. Растригин Л.А. Оптимальное проектирование как объект приложения случайного поиска.- В кн.: «Проблемы случайного поиска», Рига. «Знание», 1975. вып. 4, с. 7-17.

81. Жданок А.И., Растригин Л.А. Формальный подход к созданию адаптивной структуры поисковых алгоритмов.-В кн.: «Проблемы случайного поиска», Рига. «Знание», 1975. вып. 4, с. 48-53.

82. Растригин Л.А. Структурная адаптация алгоритмов поисковой оптимизации.-В кн.: «Проблемы случайного поиска», Рига. «Зинатие», 1976, вып. 5.

83. Декснис Г.К., Растригин Л.А. Синтез алгоритмов поисковой оптимизации методом многомерной линейной экстраполяции.-В кн.: «Проблемы случайного поиска», Рига. «Знание», 1978, вып. 7, с. 184-197.

84. Башкова Н.Н., Фролов В.Н. Имитационный подход к выбору алгоритма оптимизации.- В сб.: «Структурная адаптация сложных систем управления». Воронеж. ВПИ, 1977, с. 86-89.

85. Кудрин В.Г. Универсальная автоматизированная адаптивная система оптимизации.- «Автоматика и вычислительная техника», Рига. «Знание», 1977, вып. 4.

86. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. М. «Наука», 1965.

87. Веретенников Л.П., Ясаков Г.С. Вопросы синтеза автономных электроэнергетических систем по условию качества переходных процессов.: Электричество, 1977, №10, с. 7-13.

88. Страхов С.В. Переходные процессы в электрических цепях, содержащих машины переменного тока. М. ГЭИ, 1960.

89. Монахов О.И. Оптимальное проектирование синхронных машин с учетом динамических свойств. Тр. ин-та инж. ж.д. трансп., МИИТ, 1982, вып. 710. с. 3-7.

90. Монахов О.И. Решение задач линейного и нелинейного программирования на ЭВМ с помощью пакетов прикладных программ. М.: МИИТ, 1988. - 44с.

91. Сборник задач по теории автоматического регулирования и управления. Под ред. Бесекерского В.А. - М.: Наука, 1978.

92. Математическое обеспечение ЕСЭВМ. Институт математики АН БССР. Минск, 1973, вып. 2, часть 2.

93. Монахов О.И., Новокрещенова Л.Д., Раскин В.В., Урдин В.И. Разработка оптимальных программ управления движением транспортных средств. Изв. Вузов «Электромеханика», 1991, №5, с. 61-66.

94. Монахов О.И., Новокрещенова Л.Д., Урдин В.И., Варнаков Н.П. Автоматизированный расчет режимных карт в депо. ж. «Электрическая и тепловозная тяга». 1989, №12, с. 12-13.

95. Костромин А.М. Оптимизация управления локомотивом. М.: Транспорт, 1979. – 119с.

96. Правила тяговых расчетов для поездной работы. М.: Транспорт, 1985. 287с.

97. Аттетков А.В. И др. Введение в методы оптимизации. М.: Финансы и статистика, 2008. – 287с.

98. Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 440с.

99. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. М.: Высшая школа, 2005. - 544с.

100. Сухарев А.Г., Тимоков А.В., Федоров В.В. Курс методов оптимизации: учебное пособие. М.: Физматлит, 2005.-368с.

101. Черногородова Г.М. Методы оптимизации. Нелинейное программирование: учебное пособие. ГОУ ВПО УГТУ.- УПИ, 2007.- 113с.

102. Ширяев В.И. Исследование операций и численные методы оптимизации. Комкнига, 2007.-216с.

103. Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. М.: Физматлит, 2003.-304с.

104. Медынский М.М., Антоний Е.В. Численные методы нелинейной оптимизации: алгоритмы и программы. Учебное пособие. М.: МАИ, 2003.-192с.

105. Нинул А.С. Оптимизация целевых функций. Аналитика. Численные методы. Планирование эксперимента. М.: Физматлит, 2009-336с.

106. Трэвис Дж., Кринг Дж. LabVIEW для всех. ДМК Пресс, 2005-544 с.

107. Загидуллин Р.Ш. Multisim, LabVIEW и Signal Express. Практика автоматизированного проектирования электронных устройств. М.: Радио и связь, 2009-366с.

Не нашли, что искали? Воспользуйтесь поиском: