Выбор независимых переменных 2 страница. Авторами предлагается набор значений параметров, входящих в алгоритм, которые (по утверждению авторов) считаются оптимальными: .

Авторами предлагается набор значений параметров, входящих в алгоритм, которые (по утверждению авторов) считаются оптимальными: .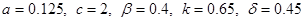

Случайный поиск с самообучением (Даниленко – Каган)

Авторами [33] был предложен эффективный алгоритм с самообучением. Предлагаемый алгоритм реализует пробные перемещения из точки 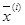в точку 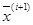по формуле

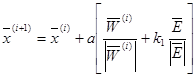(2.9)

где a- шаг поиска;

- n -мерный вектор, составляющими которого являются случайные величины, равномерно распределённые на интервале (-0.5, 0.5);

- коэффициент случайности;

- n -мерный вектор предпочтительного направления .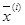

Вектор 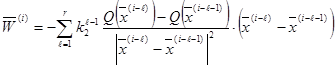, (2.10)

где - некоторый коэффициент ( <1);

r - число запоминаемых предыдущих направлений;

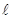- номер запоминаемого предыдущего направления (отсчёт ведётся от последнего направления к предыдущему).

В результате исследований, проведённых авторами [33] были получены численные значения параметров алгоритма .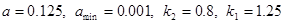

Случайный поиск с самообучением (Трахтенберг)

В статье [35], а также в книге [36] приводится эффективный алгоритм случайного поиска с самообучением. Рекуррентная формула для перемещения в пространстве оптимизируемых параметров имеет вид

(2.11)

где a – шаг поиска;

- масштабные коэффициенты;

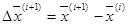- приращение вектора, которое привело к последнему удачному шагу;

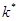- число следующих подряд неудачных шагов поиска;

- константы: .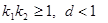

В книге [36] приведена программа, реализующая вышеизложенный алгоритм на языке ФОРТРАН-IV, а также рациональные параметры алгоритма

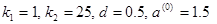
Случайный поиск со смешанной тактикой

В работе [37] предлагается для повышения эффективности поиска алгоритм со сменой тактики поиска.

Априорно определяется некоторое значение до достижения, которого ведётся поиск (стадия I)

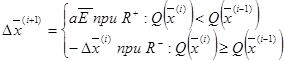(2.12)

Как только алгоритм нашел значения меньшие границы , считаем, что находимся в зоне притяжения экстремума и соответственно переходим к стадии II:

1) резко уменьшаем шаг поиска a (в 10раз);

2) переходим к алгоритму с линейной тактикой (удачный шаг повторяется)

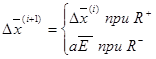(2.13)

В случае если определённое число шагов не привело к выполнению условия окончания поиска, делается большой случайный шаг и осуществляется переход к стадии I. При достижении границы смены тактики - переход к стадии II и т.д.

Экстраполяционный случайный поиск с адаптирующимся шагом

Эффективным средством повышения быстродействия поиска оказывается линейная экстраполяция. В работе [38] подобная экстраполяция распространяется на случайную последовательность продвижений в пространстве независимых переменных.

На i-ом этапе предлагаемого метода вводят итерацию, состоящую в экстраполяции по формуле

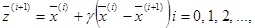(2.14)

где - коэффициент;

W – некоторый метод поиска минимума без правила останова, состоящий из m идентичных независимых итераций ω, первая из которых действует на точку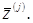

На начальном этапе (i =0) точка задается произвольно,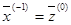

Если точка 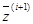удовлетворяет заданному критерию К, то она рассматривается в качестве исходной для итераций ω

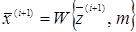(2.15)

В противном случае экстраполяция считается неудачной и метод переводится в состояние .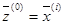

В работе [38] в качестве критерия допустимости экстраполяции К задается неравенство

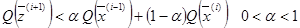(2.16)

В качестве итераций ω в предлагаемом методе использован алгоритм случайного поиска с адаптирующимся шагом, состоящий в следующем. Из каждой точки 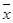осуществляют два движения 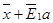и 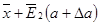, где вектор равномерно распределён на единичной сфере. Если на протяжении S попыток не было ни одного удачного движения, то величина шага уменьшается a=a×q, q<1. Итерация ω считается оконченной в случае хотя бы одного удачного движения. Конкретные значения параметров алгоритма: .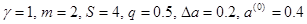

Эмпирические рекомендации относительно конкретного выбора параметров алгоритма 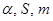таковы. Алгоритм мало чувствителен к выбору 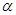вдали от экстремума: 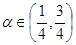. Вблизи экстремума 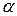следует уменьшать 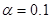. Эксперименты показывают, что величина 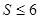, а по отношению к m >1 алгоритм в достаточной степени устойчив.

Алгоритм с перестройкой вероятностных характеристик поиска

В соответствии с алгоритмом [39] перемещение в пространстве независимых переменных можно записать в следующем виде

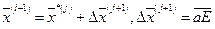(2.17)

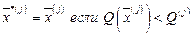
где a – длина рабочего шага;

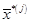- вектор оптимальных значений переменных за j предыдущих шагов;

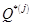- минимальное значение функции качества за j предыдущих шагов;

Самообучение проявляется в перестройке вероятностных характеристик поиска, т.е. в целенаправленном воздействии на случайный выбор направления рабочего шага – вектор . Составляющую вектора можно определить по следующей зависимости

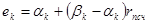(2.18)

где - случайное число, равномерно распределённое на интервале ;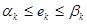

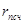- псевдослучайное число, равномерно распределённое на отрезке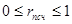

Вероятность воздействия на случайный вектор осуществляется следующим образом:

(2.19)

(2.20)

где - вероятность выбора случайного шага

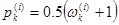
Алгоритм обучения реализуется путём соответствующего изменения параметра памяти ω при помощи следующей рекуррентной формулы

(2.21)

где - величина, определяющая скорость обучения;

- приращение k -го аргумента на i -ом шаге.

В программе предусмотрено изменение величины шага в пространстве независимых переменных в зависимости от числа удачных и неудачных шагов поиска. Рациональные значения параметров .

2.3 Градиентные методы поиска

В градиентных методах направление движения от итерации 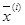к 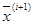определяется градиентом (антиградиентом). Частные производные критерия оптимальности, представляющие собой координаты вектора градиента, рассчитываются с помощью отношений разности значений Q в пробных точках к разности значений аргумента в этих точках.

В общем случае, когда критерий оптимальности есть функция зависящая от n переменных, для оценки частных производных служат следующие формулы:

1) 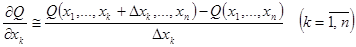(2.22)

2) 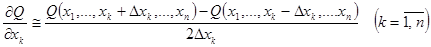(2.23)

Причём, точность аппроксимации частных производных по формуле (2.23) выше чем по формуле (2.22). Однако, при достаточно сложной связи критерия оптимальности с параметрами системы, необходимо учитывать количество вычислений градиента. При вычислении градиента по формуле (2.22), требуется (n +1) вычислений критерия оптимальности, в то время как оценка градиента по формуле (2.23) требуется 2 n вычислений критерия оптимальности. Такое большое число вычислений критерия оптимальности оправдано лишь в тех случаях, когда точность вычислений градиента имеет решающее значение для поиска экстремума функции. В данной работе градиент определяется с помощью формулы (2.22).

Подробное обсуждение градиентных методов приведено в работах [3-5, 7, 40, 41].

Прежде чем переходить к описанию методов, нельзя не отметить одного обстоятельства, которое необходимо учитывать при решении задач условной оптимизации. При учёте ограничений (1.1) и (1.2) на область поиска метод градиента и наискорейший спуск не гарантируют нахождение оптимального решения 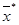. В случае нарушения ограничений требуется либо модернизация градиентных методов и поиск вдоль границы области допустимых значений независимых переменных [41], либо преобразование задачи с ограничениями при помощи метода штрафных функций и осуществление поиска решения задачи безусловной оптимизации. Вышеуказанное обстоятельство следует отнести и к рассматриваемым далее другим детерминированным методам (квазиньютоновским и др.)

Градиентный метод оптимизации

Метод градиента [3-5, 7, 40, 41] является одним из самых распространенных детерминированных методов оптимизации. Смысл его сводится к организации движения в антиградиентном (при минимизации) направлении.

Переход из состояния 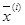в состояние 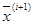осуществляется в соответствии с выражением

(2.24)

где 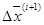- рабочий шаг, выражение для которого по методу градиента в случае минимизации имеет вид

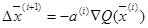(2.25)

где 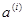- длина рабочего шага.

Остановимся подробнее на вопросе выбора величины шага 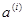. Быстрота сходимости процесса поиска минимума функции и его точность существенно зависят от выбора величины .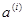

Наиболее просто реализуется метод счёта с постоянным шагом 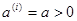. При этом на каждом шаге проверяют условие убывания функции

(2.26)

и, если оно нарушается, 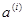уменьшают вплоть до восстановления этого условия. Величина a выбирается заранее исходя из некоторых априорных данных о задаче.

Для увеличения быстроты перемещения вдали от экстремума величину a целесообразно выбирать достаточно большой. Однако при этом в каждой новой точке поиска следует проверять условие убывания функции с тем, чтобы не перескочить за счёт большого шага точку min Q.

В данной работе длина рабочего шага поиска изменяется в соответствии с эвристическим алгоритмом [34]:

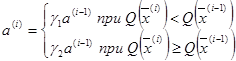(2.27)

.

В результате вычислительных экспериментов по минимизации функции при и 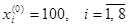были получены значения коэффициентов изменения шага поиска .

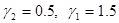Для разумного сочетания быстроты и точности предлагается чередовать грубый и точный поиск в зависимости от того, как далеко находится 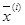от минимума . За меру близости к минимуму δ удобно принять сумму абсолютных значений производных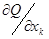

(2.28)

Введены некоторые положительные константы 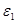и 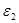(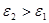) и следующие условия:

4) если , то необходим грубый поиск, т.е. поиск с большим значением коэффициентом ;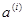

5) если , то необходим точный поиск;

6) если 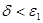, то поиск окончен.

Для построения алгоритма поиска важно определить условие окончания процесса поиска. В качестве таких условий могут быть приняты следующие:

4) пробные приращения переменных 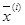обоих знаков приводят к положительному приращению функции

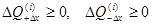(2.29)

5) приближённое значение градиента по модулю не превышает некоторой положительной величины ε, т.е.

(2.30)

При минимизации 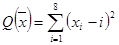значения констант 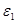и 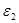были равны , .

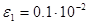Метод наискорейшего спуска

Алгоритм, реализующий метод наискорейшего спуска, состоит в следующем [41]:

1. Обращение к процедуре вычисления функции Q при заданных исходных значениях ;

2. Определение градиента

;

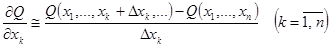3. Оценка условия окончания поиска

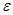- точность поиска. Если условие выполняется, то осуществляется переход к п. 6;

4. Перемещение по лучу антиградиента

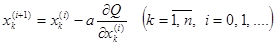
При выполнении условия 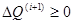перемещение по лугу антиградиента прекращается;

5. Переход к пункту 2;

6. Печать результатов

Трудоемкость (скорость сходимости к оптимальному решению) алгоритма поиска характеризуют следующие данные:

1) количество вычислений градиента ;

2) количество малых шагов перемещений по лучу градиента.

Трудоемкость алгоритма существенным образом зависит от требуемой точности решения 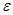и величины шага a. Длина рабочего шага поиска изменяется в соответствии с эвристическим алгоритмом, аналогично тому, как это сделано в градиентном методе. Коэффициенты изменения шага, полученные в результате 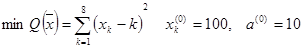, имеют значения .

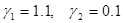2.4. Квазиньютоновские методы

В методе Ньютона [4] процесс поиска определяется как

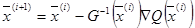(2.31)

где - гессиан, представляющий собой квадратичную матрицу вторых частных производных , взятых в точке ;

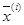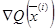- градиент в точке .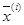

Метод Ньютона обладает значительно более высокой скоростью сходимости по сравнению с градиентными методами, но в силу двух существенных недостатков находит ограниченное практическое применение в расчётах. Первый – необходимость вычисления гессиана в каждой точке, который вычисляется с помощью конечных разностей второго порядка, требующих n(n+1)/2 вычислений, где n – размерность задачи. Второй недостаток – применение метода Ньютона в небольшой области вблизи экстремума .

В квадратичных методах первого порядка (квазиньютоновских) используется некоторая симметричная матрица 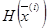, являющаяся некоторым приближением . После каждой итерации матрица 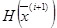вычисляется как исправление 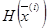с учётом информации о первых производных, полученных в течение итерации. Тогда очередное направление поиска определяется как

(2.32)

Причём использование матрицы H практически не связано с дополнительными затратами на анализ математической модели.

Характеристика квазиньютоновских методов:

6.1. минимум квадратичной функции с помощью этих методов достигается за n – шагов, где n – размерность задачи.

6.2. в случае произвольного вида, методы позволяют для заданной погрешности получить приближенное решение быстрее в ряде случаев, чем это позволяют сделать методы наискорейшего спуска и параллельных касательных;

6.3. недостатком методов является необходимость точного определения минимума на каждой итерации. Указанный недостаток ограничивает возможности методов, особенно в «овражных» ситуациях.

Метод Давидона – Флетчера – Пауэлла

Реализацией квадратичного метода первого порядка является хорошо зарекомендовавший себя метод Дэвидона – Флетчера – Пауэлла [4, 42]. Алгоритм работает следующим образом. Сначала в пространстве независимых переменных выбирают подходящую начальную точку. Затем, вычисляя составляющие градиента, определяют направление поиска

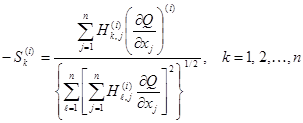(2.33)

где 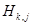- элементы симметричной положительно определённой матрицы размерности n×n

Поскольку обычно матрица заранее неизвестна, то в качестве выбирается произвольная положительно определённая (например, единичная) матрица. В этом случае поиск начинается вдоль линии наискорейшего спуска. Одномерный поиск ведётся вдоль исходного направления в соответствии с соотношением

(2.34)

где a – величина шага в направлении поиска.

Найдя одномерный оптимум, проверяют результат на сходимость и, если она достигнута, поиск прекращают. В противном случае, для дальнейшего поиска выбирают новое направление, в котором поправочная матрица определяется по следующей формуле:

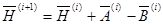(2.35)

Элементы матриц 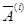и , имеющих размерность n×n вычисляются по формулам

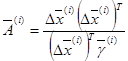(2.36)

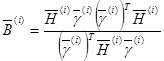(2.37)

где верхним индексом T обозначены транспонированные матрицы, а 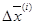и - соответственно вектор – столбцы разностей независимых переменных и градиентов в двух точках, определяемых соотношениями

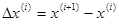(2.38)

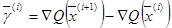(2.39)

Определив новое направление поиска, проводят одномерный поиск и продолжают итерационный процесс.

Метод сопряжённых направлений

Направления 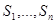называются сопряжёнными [4,7] относительно симметричной и положительно определённой матрицы G, если

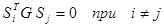(2.40)

Движение к экстремуму по сопряженным направлениям позволяет существенно ускорить поиск, поэтому в работах, направленных на развитие методов оптимизации, значительное внимание уделяется улучшению выбора сопряженных направлений.

Пусть 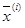и 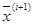- два последовательных приближения к экстремуму критерия оптимальности . Тогда с точностью до слагаемых второго порядка справедливо равенство

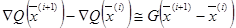(2.41)

Если направление является сопряжённым направлению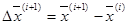

т.е. 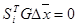, то в силу равенства (2.41) имеем

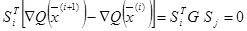(2.42)

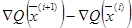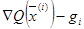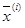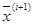Это и означает, что вектор ортогонален приращению градиента . Указанное свойство позволяет сформулировать достаточно простой вычислительный алгоритм сопряжённых градиентов. Обозначим . Разность градиентов в точках и обозначим

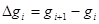(2.43)

Начальная итерация при заданном включает вычисление градиента 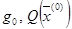и поиск минимума в направлении 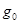. Обозначим точку этого минимума и градиент в этой точке 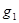. Тогда, полагая для первого из сопряжённых направлений

Не нашли, что искали? Воспользуйтесь поиском: