Выбор независимых переменных 10 страница. Оптимизация параметров СГ в АСЭ с эл.мех

Таблица 5.19

Оптимизация параметров СГ в АСЭ с эл.мех. ППС при набросе нагрузки (метод наискорейшего спуска)

N	Q
	0,516002	0,199	0,3	0,275	0,522	0,54	0,236
	0,516	0,15	0,225	0,205	0,653	0,4	0,177
	0,2043	0,15	0,225	0,205	0,653	0,4	0,177
	0,2043	0,15	0,225	0,205	0,3925	0,4	0,2272
	0,23393	0,15	0,225	0,205	0,653	0,4	0,177
	0,2043	0,15	0,225	0,205	0,653	0,4	0,177
	0,2043	0,15	0,225	0,205	0,4943	0,4	0,1806
	0,15776	0,15	0,225	0,205	0,3925	0,4	0,1842
	0,13801	0,15	0,225	0,205	0,3925	0,4	0,1878
	0,13909	0,15	0,225	0,205	0,3925	0,4	0,1873
	0,13888	0,15	0,225	0,205	0,3925	0,4	0,1868
	0,13808	0,15	0,225	0,205	0,3925	0,4	0,1842
	0,25	0,375	0,345	0,653	0,68	0,295
	0,15	0,225	0,205	0,3925	0,4	0,177

5.2.3 Оптимизация динамических свойств САУ.

Рассмотрим еще один пример применения методов полинейного программирования для оптимизации динамических свойств системы автоматического управления (САУ) [90].

Техническое задание на проектирование САУ обычно содержит ряд требований, предъявляемых к различным её характеристикам, в том числе, к показателям качества переходных процессов, динамической ошибке и т.п.

Задача получения требуемого качества переходного процесса в САУ формируется как задача параметрической оптимизации, т.е. при заданном описании объекта определить некоторые параметры САУ, обеспечивающие минимум интегральной оценки

,

где - интервал времени интегрирования;

) - результат моделирования динамики САУ;

- заданная функция времени.

Объект управления (нелинейная следящая система [91, задача 409], структурная схема которой изображена на рис. 5.7 имеет следующие значения параметров:

Статическая характеристика нелинейного звена показана на рис. 5.8, где b=0.5, c=1.5. Переходный процесс в системе рассчитывался при ступенчатом задающем воздействии . В качестве берётся изменение . Моделирование динамики системы осуществляется с использованием стандартной программы, реализующей метод Хемминга [92]. Начальные условия для переменных системы дифференциальных уравнений – нулевые. Интегрирование ведётся в интервале с шагом 0.0025 с.

Оптимизация осуществляется ведется по четырем параметрам САУ:

Результаты оптимизации различными алгоритмами НЛП сведены в таблицу 5.19. Переходные процессы в САУ с исходными параметрами и с параметрами, полученными в результате оптимизации по критерию минимума интегральной оценки, приведены на рис. 5.9. Видно, что сравнительно хорошие результаты дало применение градиентного метода, при этом постоянные времени достигли нижних границ области поиска.

Рис. 5.7 Структурная схема системы

Рис. 5.8 Статическая характеристика нелинейного звена

Рис. 5.9 Переходные процессы в САУ: с исходными параметрами (_______),

с оптимальными параметрами (n=4); метод сопряженных градиентов ();

метод случайного поиска (Даниленко – Каган) ();

метод градиента ().

Таблица 5.19

Результаты оптимизации

Общее количество шагов	Число удачных шагов	Число неудачных шагов	Значение	Значение независимых переменных	Метод оптимизации
			0,2688	2,48	0,0457	2,66	0,0979	Растригин-Тарасенко [34]
			0,2656	1,56	0,025	2,38	0,075	Градиентный [41]
			0,2677	2,56	0,0378	2,60	0,118	Даниленко Каган [33]
			0,2538	2,33	0,0357	2,58	0,112	Сопряженных градиентов [4]
			0,2395	3,37	0,025	3,39	0,0917	Севриткин [39]
До оптимиза ции			0,3261	2,33	0,074	2,58	0,126

5.3 Результаты решения тестовых задач оптимизации при использовании различных стратегий выбора поисковых методов

Разработка и применение эффективных критериев распознавания поисковых ситуаций повышает качество функционирования пакета программ оптимизации, но при этом усложняется алгоритм распознавания, увеличиваются затраты машинного времени и т.д. Таким образом, возникает вопрос о создании надежных и экономичных критериев распознавания поисковых ситуаций.

Для сравнительной оценки различных подходов к выбору методов оптимизации, определения затрат на распознавание, идентификацию поисковой ситуации и формирование решающих правил в работе проведен эксперимент на тестовой функции вида

где n - размерность пространства независимых переменных X. Решается

задача отыскания : = 0, при =i, i=1,n.

Результаты решения тестовой задачи при п=8, начальных значениях независимых переменных , , области поиска 0,1 <х_i<100, i=1,8 при различных стратегиях выбора методов оптимизации представлены в таблицах 5.20-5.22, где используются следующие обозначения:

JCN - число вычислений ;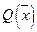

JC2, JC4 - соответственно число удачных и неудачных шагов поиска

экстремума;

- вычисленное за JCN шагов оптимальное значение функции;

- вычисленное за JCN оптимальное значение независимых

переменных.

В таблице 5.20 представлены результаты решения тестовой задачи с использованием случайного подхода, реализующего идею выбора алгоритма поиска случайным образом. После работы различных алгоритмов поиска счет был прекращен по причине исчерпания ресурса шагов поиска.

В таблице 5.21 представлены результаты реализации жестко фиксированной последовательности выбора поисковых процедур. Счет был прекращен по

причине выполнения условия

Вышеприведенные результаты расчетов в некотором смысле демонстрируют достоинство адаптивного подхода [64-66] к выбору алгоритмов оптимизации.

Таблица 5.20

Результаты решения тестовой задачи с использованием случайного подхода

Метод оптимизации	JСN	JС2	JC4		Значение независимых переменных
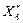
Исходная точка
Растригин – Рипа				9119,5	0,1	0,1	0,1	0,1		4,1	0,1	4,1
Давидон – Флетчер – Пауэлл		-	-	145,01	0,1	0,1	0,1	0,1	6,95	4,1	17,5	7,8
Трахтенберг				86,816	2,84	0,1	0,1	0,1	5,99	4,1	17,5	7,8
Наискорейший спуск				80,426	2,77	0,121	0,131	0,143	5,92	0,164	10,8	9,19
Трахтенберг				71,526	2,24	0,1	0,165	0,1	5,43	0,769	10,8	9,79
Растригин - Тарасенко				62,724	2,14	0,225	0,895	0,174	5,79	1,19	10,4	9,95

Остановка по причине исчерпания ресурса шагов оптимизации.

Таблица 5.21

Результаты решения тестовой задачи с использованием детерминированного подхода

Метод оптимизации	JCN	JC2	JC4		Значения независимых переменных
Исходная точка
Метод наискорейшего спуска				55,935	0,10	0,10	0,10	0,10	3,22	3,22	3,22	6,3
Метод сопряженных градиентов		-	-		0,997	2,03	3,0	4,03	4,98	5,97	6,98	7,9

Остановка по причине выполнения условия: < ; =0,10

Таблица 5.22

Результаты решения тестовой задачи с использованием адаптивного подхода

Метод оптимизации	JCN	JC2	JC4		Значения независимых переменных
Исходная точка
Метод градиента					0,995	1,99	2,99	3,99	5,0	6,0	7,0	8,0

Остановка по причине выполнения условия: < ; =0,10

5.4. Методика использования алгоритмов НЛП в задачах разработки энергооптимальных программ движения поездов на тепловозной тяге

Одним из путей экономии дизельного топлива является совершенствование режимов ведения поездов на тепловозной тяге, что определило цели и этапы работы по автоматизации разработки оптимальных программ ведения поездов выполненной кафедрой ''Управление и информатика в технических системах'' Московского института инженеров железнодорожного транспорта совместно с Прибалтийской железной дорогой [93, 94]. Кроме того энергооптимальное управление тесно связано с вопросом определения научнообоснованных норм расхода топлива. Существующие методы разработки рациональных режимов ведения поездов, связанные с опытными поездками и являющиеся обобщением опыта классных машинистов, нельзя признать совершенными, т. к. нет уверенности, что разработанные режимы являются оптимальными. В свете вышеизложенного в данном разделе описано решение задачи создания расчетной методики формирования оптимальных программ ведения поездов на тепловозной тяге с применением ЭВМ, позволяющей автоматизировать процесс расчета.

Задача оптимального управления движением поезда формулируется следующимобразом: для поезда, ведомого тепловозом определенного типа с заданным составом, необходимо найти такое управление (функцию позиций контроллера машиниста по пути), которое обеспечивает движение поезда на заданном участке при соблюдении задаваемых ограничений на скорость движения и расписание прохождения отдельных станций с минимальным расходом топлива. Характерной особенностью данной работы по сравнению с подобными, например [95] является то, что синтез оптимальных программ ведения поезда осуществляется на математической модели, учитывающей переходные процессы по силе тяги тепловоза и по расходу топлива. Такой учет позволяет создать адекватную реальному объекту математическую модель, используемую в дальнейшем для синтеза оптимального управления.

Использование математического моделирования потребовало разработки математической модели объекта управления, разработки алгоритма и программы тяговых расчетов на ЭВМ, проверки адекватности разработанной модели.

Осуществлена проверка адекватности разработанной модели путем сравнения экспериментальных и рассчитанных на ЭВМ кривых скорости, а также экспериментальных и расчетных времен прохождения станций при одном и том же управлении .

В результате проверки адекватности модели, проведенной для одного из участков Прибалтийской железной дороги протяженностью 30 км, установлено, что кривые по скорости практически совпадают, а разность экспериментальных и расчетных времен прохождения станций не превышает ±0,5 мин, что позволяет сделать вывод об адекватности разработанной математической модели пассажирского поезда на тепловозной тяге в части траектории движения. Что касается точности сравнения расчетного значения расхода топлива по сравнению с экспериментальным, то получение таковой в условиях депо не представляется возможным.

Для решения сформулированной задачи оптимального управления может быть применен один из современных методов расчета оптимального управления. Однако использование аппарата вариационного исчисления затруднительно из-за большого числа ограничений. Применение дискретного варианта динамического программирования требует высокого быстродействия и большого объема памяти ЦВМ, а использование принципа максимума связано с проблемой выбора начальных значений -функций. Поэтому в данной работе было решено использовать аппарат нелинейного программирования, применение которого не встречает трудностей при реализации поставленной задачи на ЦВМ.

Из множества методов НЛП [4] в данной работе используется метод случайного поиска, заключающийся в случайном формировании управления и пошаговом запоминании таких его значений, при которых обеспечивается минимум критерия оптимальности при отсутствии нарушений ограничений. При нарушении отмеченных ограничений производится коррекция управления, которая заключается в следующем:

1) при отставании от графика прибытия на станцию производится формирование нового вектора управления, заключающееся в последовательном повышении позиций контроллера до тех пор, пока не будет достигнута заданная точность соблюдения графика;

2) при опережении графика с вектором управления производится операция обратная вышеописанной в п. 1;

3) при нарушении ограничений по скорости производится снижение позиций контроллера до тех пор пока движение по перегону будет производиться без этих нарушений.

Разработанная математическая модель (метод случайного поиска с коррекцией управления, неполный перечень способов которой приведен выше), были положены в основу программы, разработка которой велась с использованием языка Фортран-IV. В качестве исходных данных в программе задаются: тяговые и теплотехнические характеристики тепловоза и параметры состава, профиль участка, ограничения по скорости, расписание движения по станциям и др. Результатами расчетов по разработанной программе позиции контроллера машиниста, скорость и время расхода топлива. По разработанной программе были проведены многочисленные расчеты оптимального управления (S) для ряда пассажирских поездов различных участков Прибалтийской ж.д.

Проведение расчетов исключительно для пассажирских поездов связано, во-первых, с более строгим соблюдением графика в пассажирском движении, во-вторых, с определенностью веса пассажирского состава, в-третьих, с меньшей длиной пассажирского поезда по сравнению с грузовым, что существенно в смысле адекватности разработанной математической модели. Относительно численных значений исходных данных следует сказать, что характеристики тепловоза определены по данным депо Засулаукс Прибалтийской ж.д., параметры состава пассажирского поезда и времена прохождения станций определены по расписанию движения пассажирских поездов. Профиль пути по всем используемым участкам получен в Управлении Прибалтийской ж.д.

Каждый расчет оптимального управления заканчивался по заданному числу итераций. Увеличение этого числа вело к уменьшению расхода топлива, однако при этом увеличивались затраты машинного времени. Отладочные расчеты показали, что рекомендуемое число итераций составляет от 100 до 500.

Получающееся в результате расчетов оптимальное управление, содержит частые переключения с одной позиции на другую и при ручном управлении требует повышенного внимания от машиниста. Поэтому для упрощенного управления (в смысле меньшего числа переключений контроллера машиниста) производится сглаживание полученного управления. «Сглаженное» управление имеет незначительное превышение расхода топлива, но существенно меньшее число переключений. Расчетная экономия дизельного топлива для указанного участка составила 7%.

Не нашли, что искали? Воспользуйтесь поиском: