Выбор независимых переменных 5 страница. В терминологии работы [43] «овраг» означает, что кривизна функции существенно отличается для различных направлений

В терминологии работы [43] «овраг» означает, что кривизна функции существенно отличается для различных направлений, т.е. поверхности постоянного уровня критерия оптимальности сильно вытянуты в одних направлениях и сжаты в других. Направления малой кривизны соответствуют движению вдоль «оврага», в то время как направления с большой кривизной соответствует движению поперёк «оврага». Кривая, вдоль которой вытянуты линии уровня, называется «дном оврага». «Дно оврага» для функции

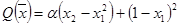
представляет собой кривую второго порядка. «Дно оврага» функции

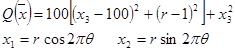
образует спираль.

Для поиска оптимума при наличии «оврагов» многие методы оказываются неэффективными и часто требуется разработка специальных, более сложных алгоритмов.

Пусть функция дифференцируема и хорошо организована, т.е. независимые переменные хорошо разделимы на группы существенно и несущественно влияющих на [86]. Тогда критерий распознавания ситуации «овраг» следующий:

(3.4)

Причём 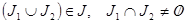, - множество индексов

При выполнении условия (3,4) , в противном случае - . Для плохо организованных систем применение условий (3.4) не приведёт к успеху. В этом случае проделывается следующая процедура. Из точки 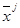производится покоординатный просмотр точки 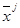с шагом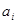

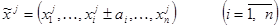(3.5)

и определяются значения функции качества 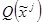. Размерность оврага будет равна , если найдётся m значений 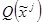удовлетворяющих условию при поиске минимума

(3.6)

где 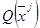- функция качества в исходной точке ,

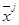>0 – коэффициент, характеризующий наклон «дна оврага»;

k – число экспериментов.

При выполнении условия (3.6) приращение по соответствующей координате запоминается и таким образом определяется направление дна оврага. Систематически проделывая описанную процедуру, имеется возможность достаточно точно отслеживать изгибающееся «дно оврага». При выполнении условий (3.5) (3.6) .

Ситуация (многоэкстремальность)

Многоэкстремальность оптимизируемой функции очень часто характеризуются априорными сведениями о ней. Однако, если о количестве локальных экстремумов информация отсутствует (что нередко чаще всего имеет место в задачах оптимального проектирования), тогда логично предложить следующую процедуру определения унимодальности . При поиске минимума производится спуск из m начальных точек, равномерно расположенных в допустимой области независимых переменных причём 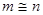. Если из начальных точек спуск приводит в одну и ту же окрестность 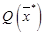точки экстремума , то считаем, что экстремум найден с определённой степенью достоверности

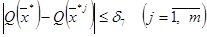(3.7)

При нарушении условия (3.7),

Ситуация (сложность объекта оптимизации)

Исследуемые объекты проектирования описываются системой алгебро-дифференциальных уравнений и, как уже указывалось, время вычисления функции объекта (заключающейся в численном решении алгебро-дифференциальных уравнений с использованием того или иного численного метода) достаточно велико.

Если время вычисления значения (время выполнения одной итерации) больше, чем реализация одной итерации поискового алгоритма (алгоритмов)

(3.8)

этот факт свидетельствует о сложности объекта оптимизации. Критерий распознавания ситуации представлен условием (3.8). При выполнения условия (3.8) .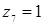

Совокупность признаков 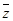даёт возможность построить гибкую систему оптимизации с распознаванием поисковой ситуации и выбором соответствующего поискового алгоритма. В общем случае, решающие правила выбора могут быть записаны для каждого алгоритма в виде

где 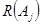- принимает при соответствующем наборе 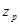значение равное либо 1 и разрешает выбор алгоритма для данной ситуации, либо 0 –в противном случае.

3.4 Выбор алгоритмов оптимизации

на основе априорной информации

В настоящем разделе приведена некоторая оценка методов оптимизации, не претендующая на полноту и конкурирование с множеством появившихся в последнее время классификаций, но дающая некоторую ориентировку в пространстве разработанных методов. Ниже предлагаются существенные вопросы, ответ на каждый из которых позволит из множества методов выбрать некоторый, приводящий к решению задачи [73 ]:

1. Производится ли сведение задачи оптимизации с ограничениями к задаче на безусловный экстремум или непосредственно анализируются заданные ограничения;

2. Приближение к оптимизму строится изнутри или извне допустимой области

1)

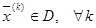
3. Является ли процедура поиска глобальной или локальной;

4. Является ли процесс формирования точек детерминированным или используется случайный выбор некоторых элементов процесса;

5. Является ли метод адаптируемым к накопленной в процессе поиска информации.

1. По исходной экстремизируемой функции могут быть построены функции

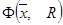
(где R – коэффициент штрафа) обладающие тем свойством, что решение задачи отыскания 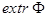более «удобно» для решения исходной задачи с ограничениями (на условный экстремум). Идея штрафных функций подкупает своей методической простотой, и за последние годы появилось огромное число статей и книг, где предлагаются различные варианты введения штрафа и исследуются теоретические вопросы сходимости предлагаемых методов. Для всех этих методов необходимо многократно отыскивать минимум функции 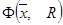, что является нелёгкой задачей.

Прекрасное описание теоретических и практических методов штрафных функций содержится в книге [24 ]. Несмотря на их широкое распространение, многие авторы считают, что переход к штрафным функциям искусственно вводит усложнённую структуру в целевую функцию, приводит к появлению сложных для минимизации «оврагов», практически исключает использование интуиции проектировщика на стадии анализа результатов счёта и организации алгоритма.

Поэтому целесообразно не пользоваться методами штрафных функций, а минимизировать , проверяя выполнение условий 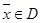и не менять алгоритм генерирования очередной точки последовательности 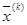при нарушении этих условий.

2. И в рамках методов штрафных функций, и в рамках других методов естественно различать процессы внутренней () и внешней () минимизации. Характерными представителями методов внутренней минимизации являются методы возможных направлений. Они позволяют выбрать в фиксированной точке 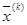допустимой области D такое направление, при котором не нарушается ни одно ограничение и функция качества монотонно убывает, т.е. причём . Различные варианты этих методов описаны в [74 ].

3. Использование локальных методов поиска возможно лишь тогда, когда предварительно известна одноэктремальность рассматриваемой задачи. В противном случае, как это имеет место в большинстве задач оптимального проектирования, необходимо применять глобальный поиск – внутри области за счёт соответствующих изменений правил выработки следующей точки или вне области – за счёт применения последовательности локальных процедур, начинающихся из разных, случайно выбранных точек.

4. Выше была отмечена необходимость использования элементов случайности для поиска глобального оптимума. Это даёт основания считать, что в той или иной мере случайность всегда должна присутствовать в алгоритмах оптимизации (либо в случайном выборе некоторых элементов поиска, либо в случайном переключении разных эвристических правил организации процесса).

5. Использование методов, адаптирующихся к результатам поиска и изменяющих правила построения последовательности 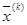в зависимости от результатов, предпочтительнее использования алгоритмов с жесткой фиксированной структурой. Поэтому при решении задач оптимизации следует применять алгоритмы с адаптацией или самообучением. Результатом проведённого анализа является обоснование того, что для решения многих задач оптимального проектирования целесообразно использование глобальных методов, основанных на сочетании детерминированных и случайных алгоритмов, адаптирующихся к результатам поиска и использующих только сведения об оптимизируемой функции и ограничениях.

Рекомендации по выбору алгоритмов на основе априорной информации не исчерпываются вышеприведёнными. Следует отметить работы [3-8, 42, 75], где даются рекомендации выбора подходящего алгоритма на основе топологических свойств исследуемой поверхности, учёта времени решения задачи на ЭВМ, сложности программирования и др.

При выборе методов оптимизации на основе априорной информации следует остановиться на особенностях методов, частично рассматриваемых в разделе 2.5.

Важную роль в процессе оптимизации играет начальная точка поиска , разумное задание которой в большинстве случаев практически невозможно. Неудачно выбранное значение вектора может привести к значительным затратам машинного времени и, в худшем случае, к тому, что экстремум функции за приемлемое время не будет найден. Одним из наиболее простых методов начального приближения является метод случайного поиска. Недостатком его использования является отсутствие априорных оценок числа испытаний, необходимых для обнаружения точки, лежащий в окрестности минимума.

Методы первого порядка (градиентный, наискорейшего спуска и др.) дают хорошие результаты на начальной стадии оптимизации, когда найденная начальная точка имеет достаточно большое значение. Для определения направления спуска требуется, как минимум, (n+1) вычисление оптимизируемой функции, где n – размерность пространства независимых переменных. Поэтому применение этих методов в случае ограниченного ресурса числа вычислений оптимизируемой функции нецелесообразно. С уменьшением величины градиента падает точность и уменьшается скорость сходимости. В этом случае, если не представляется возможным повысить точность, что связано с увеличением машинного времени, необходимо использовать методы второго порядка.

К таким методам относятся метод Ньютона, Давидона – Флетчера-Пауэлла и другие, использующие для определения направления спуска матрицы вторых производных оптимизируемой функции. Их достоинством является квадратичная сходимость в окрестности минимума. Однако эти методы требуют высокой точности вычислений вторых производных, что всё труднее выполнять вблизи точки оптимума. Кроме того, они требуют значительных затрат машинного времени, как минимум вычислений для определения направления спуска.

Чтобы избежать основной сложности методов направленного поиска – потери точности вычисления производных вблизи точки оптимума – на последнем этапе оптимизации эффективно использовать методы прямого поиска, которые обеспечивают достаточную точность вблизи оптимума, но имеет низкую скорость сходимости.

Вышеописанная очередность применения поисковых методов на различных этапах решения задачи оптимизации может быть использована в дальнейшем в качестве одной из стратегии выбора методов оптимизации. Учитывая, что указанный выбор производится на основе информации, полученной из опыта решения ряда задач различными авторами, то данная стратегия выбора методов, используемая в дальнейшем, получила название «по опыту».

Рекомендации по выбору методов оптимизации

Сравнительный анализ работоспособности и эффективности методов оптимизации, проведенный как в нашей стране, так и за рубежом не позволяет априори утверждать, что один метод заведомо лучше другого. По этой причине приводимые в литературе рекомендации правил выбора методов оптимизации являются ориентировочными. Тем не менее, общая тенденция не вызывает сомнений: наиболее эффективными являются методы первого и второго порядков (использующие соответственно первые и вторые производные критерия оптимальности ), а наименее эффективными – методы нулевого порядка (использующие только значения ) [8].

В результате анализа сравнительной эффективности методов НЛП нулевого, первого и второго порядков могут быть предложены следующие рекомендации [4, 8, 42]:

1. Методы нулевого порядка. Метод Розенброка довольно стабилен, быстро подходит к области экстремума. При числе оптимизируемых параметров n больше 10 превосходит метод Нелдера – Мида. Метод Пауэлла обладает очень хорошими результатами. В задачах оптимизации предпочтительным является использование методов Розенброка и Нелдера – Мида.

2. Методы первого порядка. Самым лучшим по сходимости и стабильности является метод Ньютона – Рафсона, но этот метод наряду с методом тяжёлого шарика целесообразно применять при наличии аналитических выражений первых производных.

Среди методов переменной метрики одним из лучших является метод Давидона – Флетчера – Пауэлла, который по быстродействию в 2-6 раз превосходит метод Розенброка.

Метод Флетчера – Ривса, совпадающий с методом сопряжённых градиентов обладает лучшей сходимостью на квадратичных функциях, но на других даёт худшие показатели.

При числе оптимизируемых параметров n больше 20 вышеперечисленные методы требуют большого числа вычислений (более 1000).

14) Методы второго порядка. Метод Ньютона находит минимум квадратичной функции за один шаг, однако этот метод не получил широкого распространения по причине квадратичного роста потерь на поиск с увеличением размерности n.

15) Повышенной надежностью и точностью обладает гибридные алгоритмы [64-66], реализованные в программах и [63].

Многие из перечисленных выше методов нулевого, первого и второго порядков реализованы в виде стандартных подпрограмм пакета SSP и описаны в [62-63].

3.5 Выбор алгоритмов оптимизации в процессе поиска

Для решения задачи выбора алгоритма адекватного данной поисковой ситуации могут применяться различные подходы. Выбор алгоритма может осуществляться:

1. на основе статистики работы алгоритма в аналогичных ситуациях;

2.на основе теоретического доказательства эффективности алгоритма для

данной поисковой ситуации;

3.на основе сравнительного анализа функционирования ряда алгоритмов в процессе вычислений;

4.на основе адаптивного подхода.

В целях повышения надежности выбора адекватного алгоритма оптимизации в системе оптимального проектирования используются комбинации способов выбора.

Рассмотрим сравнительные характеристики двух больших групп методов: детерминированных первого порядка и случайных. Каждый шаг поиска в итеративных методах включает два основных этапа:

1) выбор направления движения в пространстве независимых переменных;

2) выбор величины перемещения в найденном направлении.

Выбор направления движения в детерминированных методах первого порядка связан с вычислением . Величина шага выбирается заранее или вычисляется. В методах случайного поиска выбор направления движения и величины пробных и рабочих шагов зависят от реализации некоторого случайного процесса. Хорошо обоснованной является общая рекомендация об использовании методов случайного поиска в задачах большой размерности вдали от точки минимума, когда хорошо аппроксимируется линейной функцией и для определения квазиградиентного направления нет необходимости вычислять n значений функций (как в градиентных методах), а их можно определить по значениям в m точках (m<n), выбираемых случайно. Вблизи точки минимума эффективность случайного поиска существенно снижается.

Поэтому области экстремума наиболее эффективно применение квадратичных методов, позволяющих найти точку минимума с большей точностью и использующих при этом меньшее число итераций, чем случайные методы. Сходимость квадратичных методов гарантируется только при хороших начальных приближениях, находящихся в области притяжения точки минимума 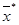. Таким образом, приходим к следующей стратегии поиска:

1) вдали от точки минимума используются случайные методы поиска;

2) в переходной области с помощью детерминированных методов первого порядка выходим в окрестность ;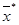

3) в окрестности минимума переходим на детерминированный квадратичный метод.

Поверхность функции качества многих решаемых задач автоматизации проектирования имеет овражный характер, что приводит к необходимости применения специальных «овражных» методов в окрестности минимума.

Вышеописанный подход к оптимизации объекта с жестко фиксированной последовательностью выбора поисковых методов называется детерминированным.

Второй подход - адаптивный – связан с выбором алгоритма в соответствии с решающей функцией для системы признаков, характеризующих поисковую ситуацию.

Третий подход, случайный, реализует идею выбора случайным образом поискового алгоритма с вероятностью , где L – общее число алгоритмов библиотеки оптимизации.

Кроме того, не исключается возможность выбора определённых алгоритмов оптимизации по желанию инженера – проектировщика.

Рассмотрим более подробно адаптивный подход к выбору алгоритму. Определение эффективности различных поисковых алгоритмов в вышеуказанных поисковых ситуациях осуществляется, как правило, экспериментальным путём на основе сопоставительного анализа для различных тестовых функций [14 – 22 ].

Путём анализа можно определить допустимую область каждого из включённых в библиотеку алгоритмов в виде решающих функций

На основе сопоставительного анализа работоспособности и эффективности алгоритмов оптимизации, произведён выбор эффективных, достаточно просто реализуемых алгоритмов. Подробное их описание приведено в главе 2.

Класс алгоритмов случайного поиска

1) с адаптацией шага (Растригин – Тарасенко);

2) с самообучением (Келли – Уиллинг);

3) с самообучением (Растригин – Рипа);

4) с самообучением (Даниленко – Каган);

5) с самообучением (Трахтенберг);

6) со смешанной тактикой;

7) с экстраполяцией;

8) с перестройкой направления рабочего шага (Севриткин).

Решающее правило для выбора алгоритма случайного поиска может быть записано в следующем виде

Класс методов первого порядка

(использующих производные )

9) градиентный;

10) наискорейшего спуска.

Данные методы эффективны в ситуациях «крутой спуск» (подъем). Решающие правила для выбора алгоритмов следующие

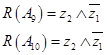
Класс квазиньютоновских методов

11) алгоритм Давидона – Флетчера - Пауэлла.

Данный метод эффективен при минимизации квадратичных целевых функций при размерности задачи n < 10

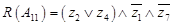
12) алгоритм сопряжённых градиентов.

Предпочтителен при оптимизации квадратичных целевых функций при размерности задачи n > 10

Овражные методы поиска

13) статистический градиент (Волынский – Филатов)

Алгоритм содержит элементы адаптации длины рабочего шага, адаптирующей в соответствием с характером изменения функции качества

14) алгоритм с регулируемой величиной спуска

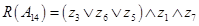
15) метод оврагов (Павлов – Солдатов)

Глобальный поиск

16) коллективом автоматов Буша – Мостселлера (Короп)

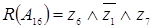
17) с независимым выбором плотности распределения случайных шагов

3.6 Повышение эффективности решения оптимизационных задач на основе применения методов планирования экспериментов

Методы планирования эксперимента первоначально были разработаны для планирования проводимых в условиях помех экспериментов по определению параметров управляющих воздействий, обеспечивающих оптимизацию технологического процесса.

Вычисление с помощью ЦВМ значения критерия оптимальности в некоторой точке пространства независимых переменных на основе модели проектируемого объекта может также рассматриваться как некоторый численный эксперимент.

Если модель проектируемой системы довольно сложна, то требуется значительное время для проведения численного эксперимента. Для упрощения исходной математической модели и, соответственно, снижения затрат машинного времени на её анализ используется аппарат теории планирования эксперимента [86].

Методы этой теории необходимы для представления показателей качества переходных процессов в виде полиномов, в которых аргументами являются исследуемые параметры системы.

Таким образом, применение теории планирования эксперимента позволяет относительно просто для сложных систем управления получить аналитические зависимости показателей качества динамических свойств системы от её параметров. Затем может решаться общая задача нелинейного программирования по выявлению параметров системы, обеспечивающих экстремум выбранных показателей качества.

Методы планирования эксперимента позволяют также сократить объём вычислений за счёт отсеивания тех параметров, изменение которых не даёт существенного изменения критерия оптимальности. С этой целью проводятся так называемые отсеивающие эксперименты. Если значение критерия оптимальности мало изменяется при изменении отдельных параметров на уровнях минимальном и максимальном, то соответствующие параметры временно исключаются из рассмотрения. В результате уменьшается размерность пространства поиска, что ускоряет движение к оптимуму. При этом после определённого числа шагов необходимо проверить, следует ли расширить пространство поиска введением ранее исключённых переменных [86].

Рассмотрим более подробно применение теории планирования эксперимента для представления показателей качества переходных процессов в полиномиальной форме:

(3.9)

где 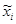- исследуемые параметры системы;

- их основные уровни;

- интервал варьирования;

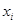- те же параметры системы, но центрированные и масштабированные т.е. в относительных единицах (факторы) [86]

- число параметров;

- коэффициенты.

Применение планирования эксперимента предусматривает искусственное варьирование параметров системы по матрице планирования и практически возможно только на моделях. К параметрам планирования можно отнести количество переменных, интервал варьирования, основные уровни и величину звёздного плеча для планирования второго порядка [86].

Не нашли, что искали? Воспользуйтесь поиском: