Выбор независимых переменных 4 страница. АСОПР – автоматическая система оптимального проектирования [68] разработана в МАИ в рамках операционной системы ОС ЕС

АСОПР – автоматическая система оптимального проектирования [68] разработана в МАИ в рамках операционной системы ОС ЕС. Она предназначена для выбора оптимальной стратегии поиска решения оптимизационных задач, для чего процесс решения последних разбивается на ряд подзадач, которыми могут служить поисковые ситуации, возникающие при исследовании функций многих переменных.

Выбор предпочтительного метода производится на основе анализа эвристических оценок эффективности алгоритмов оптимизации.

Для обеспечения возможностей использования пакетов программ оптимизации специалистами разной квалификации и в различных прикладных областях необходимо иметь модули, осуществляющие в зависимости о поисковой ситуации в оптимизационной задаче выбор наиболее эффективного метода и, таким образом, обеспечивающие адаптацию пакета к решаемой задаче. В рамках отмеченной проблемы в пакетах программ оптимизации используются блоки «накапливания опыта» [69-71], в которых собирается статистика по решаемым задачам, что позволяет выработать рекомендации по использованию метода.

В [72] описан пакет оптимизационных программ со структурной адаптацией “ASTROP”, разработанный на алгоритмическом языке ПЛ-1 для работы в ОС ЕС ЭВМ.

Общая характеристика блока параметрической оптимизации пакета прикладных программ СПАРС, разработанного на языке ФОРТРАН – IV в Киевском политехническом институте даётся в [73].

Вышеизложенное не исключает возможности использования для решения задач оптимизации отдельных программ пакета SSP, среди которых необходимо выделить программы и , реализующие гибридные алгоритмы [64-66].

3. Эффективность поисковых методов оптимизации и рекомендации по их выбору

В условиях повышения эффективности научных исследований решение задач оптимального проектирования предполагает наличие априорной информации об эффективности алгоритмов поиска, их предпочтительной области применения, рациональных параметров и др. Такая информация накапливается на основе наблюдений за функционированием алгоритмов оптимизации в тестовых задачах, а также на основе теоретических исследований. Возможности получения такой информации осложнены тем, что, несмотря на бурное развитие, аппарат нелинейного программирования в настоящее время нельзя считать окончательно сформированным. Всё ещё ведётся разработка новых и совершенствование существующих методов оптимизации. Этими обстоятельствами в значительной мере объясняется и отсутствие общепринятой классификации алгоритмов НЛП, хотя варианты такой классификации, разработанные в соответствии с различными принципами, имеются [2-4, 6 ].

За разработкой новых эвристических алгоритмов не следует конкретных рекомендаций по их применению, что заставляет инженера-проектировщика колебаться перед выбором нужного ему алгоритма. При этом трудность выбора заключается в том, что:

4) лишь немногие методы исследованы аналитически, причём результаты получены для выпуклых или квадратичных функций;

5) экспериментальное сравнение проводится на разных классах тестовых функций с использованием различных критериев эффективности.

Сравнительной оценке функционирования поисковых алгоритмов посвященных работы [14-22].

Однако, в силу различных подходов к оценке эффективности алгоритмов целостной и полной картины сравнительных характеристик методов НЛП в настоящее время нет.

В данной работе автор не ставит своей целью восполнить пробел в данной области (хотя некоторые результаты сопоставительного анализа поисковых алгоритмов приведены в главе 2), а рассматривает пути повышения эффективности решения оптимизационных задач.

Ниже обсуждаются критерии оценки эффективности и рассматриваются вопросы уменьшения затрат машинного времени на решение задач оптимизации за счет введения адаптации в алгоритмы поиска, а также перехода от сложных математических моделей к простым аппроксимирующим выражениям на основе аппарата планируемого эксперимента.

3.1 Оценка эффективности алгоритмов оптимизации

Эффективность алгоритма отражает возможность достижения с его помощью конечной цели при поиске оптимального решения [6]. Эффективность поиска обуславливается природой задачи: степенью нелинейности, размерностью, топологией функции отклика и т.д. В не меньшей мере эффективность зависит от «деталей» алгоритма и машинной программы.

Эффективность программы оптимизации, в основном, определяется временем минимизации , которое грубо можно определить как

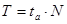
где - время, затрачиваемое на решение задачи анализа системы (время вычисления значения )

- число вариантов расчёта.

Следовательно, эффективность использования ЭВМ при оптимальном проектировании связана с уменьшением затрат машинного времени на вычисление функции качества, а также надежным осуществлением поиска за минимальное (или приемлемое) число шагов. Эта проблема является чрезвычайно важной для всех практических применений поисковых алгоритмов, когда вычисление связано (в силу сложности моделей исследуемых систем) с большими затратами машинного времени.

Поиск общего решения этой проблемы – сложная задача. Попытаемся рассмотреть её с точки зрения выбора рационального алгоритма оптимизации. Как уже указывалось, ни один из методов НЛП не может считаться наилучшим по сравнению с другими алгоритмами при решении любых задач оптимизации. Таким образом, возникает вопрос выбора критерия оценки эффективности того или иного метода НЛП в конкретных условиях.

Наиболее важными критериями оценки эффективности алгоритмов являются [3, 6 ].

7) точность поиска, т.е. значение окрестности локального оптимума 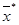, в которую приводит алгоритм оптимизации после заданного числа итераций;

8) скорость сходимости, т.е. число итераций, необходимое для достижения заданной точности;

9) время поиска на ЭВМ оптимально решения;

10) стабильность (или устойчивость), которая характеризуется незначительным увеличением числа итераций при малых возмущениях, возникающих при выборе начальной точки, вследствие погрешности вычислений и т.д.

11) надёжность, т.е. отыскание алгоритмом экстремума при многократном повторении поиска из различных начальных точек;

12) простота машинной программы, реализующей алгоритм;

13) простота практического использования алгоритма (время, необходимое для подготовки и ввода исходных данных).

Аналогично тому, как это сделано в задачах многокритериальной оптимизации эффективность поисковых алгоритмов может быть оценка обобщённым критерием [42]

где - время, затраченное на поиск экстремума n-мерной функции из начальной точки с помощью алгоритма с параметрами , а точность поиска задается .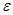

Наилучший алгоритм поисковой оптимизации определяется из решения задачи отыскания максимума К.

Теоретическое решение сформулированный задачи, по существу, получено лишь для алгоритмов поиска экстремума одномерных унимодальных функций [ 24 ].

В более сложных ситуациях сравнение алгоритмов и выбор из них наилучшего проводятся на основе экспериментальных исследований [14-22 ].

В задачах автоматизации проектирования основными критериями эффективности алгоритмов (используемыми и в настоящей работе) – точность поиска и объём вычислений.

Оценка алгоритмов по точности поиска производится путём вычисления локальных характеристик для двух последовательных итераци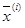й и :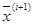

Характеристики ε и δ отражают степень приближения к оптимуму, как по координатам вектора независимых переменных , так и по критерию оптимальности .

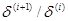Для контроля эффективности на каждом шаге вычисляются отношения и , которые должны быть меньше единицы. Если эти отношения стремятся к единице, метод поиска следует модифицировать или заменить более эффективным.

Кроме того, итерации с использованием некоторого выбранного в соответствии с наперед заданными условиями алгоритма продолжают до использования отведённых ресурсов по объёму вычислений. При исчерпании ресурса производится смена алгоритма.

Критерии эффективности методов оптимизации

Для решения задачи оптимизации можно воспользоваться различными алгоритмами. Это приводит к тому, что до решения задачи исследователю необходимо ответить на следующие вопросы:

1) какой алгоритм выбрать для решения задачи?;

2) какой алгоритм считать наилучшим?.

Целесообразность выбора того или иного алгоритма в целях его практического использования определяется эффективностью этого алгоритма при решении конкретных задач оптимизации. Прежде чем переходить к оценке эффективности конкретных алгоритмов НЛП, рассмотрим критерии эффективности алгоритмов оптимизации.

При выборе алгоритма решения конкретной задачи оптимального проектирования (например, оптимизации автономных энергосистем) ориентируются на некоторые математические свойства критерия оптимальности , где 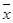- вектор оптимизируемых параметров объекта исследований.

Для выбора известных и разработки новых алгоритмов, оценки их эффективности служат тестовые функции. Наибольшую группу среди них представляют двумерные функции, моделирующие различные «рельефы» . Ко второй группе относят многомерные текстовые функции. К третьей группе можно отнести многомерные функции, использующие идею метода штрафов.

К числу важных критериев, используемых при оценке эффективности алгоритма оптимизации на том или ином классе тестовых функций, относятся:

1) точность поиска;

2) скорость сходимости;

3) время машинного счёта;

4) простота машинной программы и др.

Наиболее широко используемым критерием при оценивании относительной эффективности методов НЛП, является количество вычислений , требуемое для получения оптимального решения с заданной точностью:

,

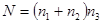где 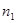и 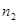- количество вариантов анализа соответственно для вычисления оптимизируемой функции и для определения направления поиска;

- количество шагов поиска.

При детерминированных критериях оптимальности . Значение 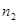зависит от размерности задачи n и порядка метода оптимизации. В методах нулевого порядка производные критерия оптимальности по параметрам не используются и . В методах первого порядка 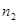соответствует количеству вычислений, необходимых для определения первых производных. Так, при определении составляющих градиента критерия или В методах второго порядка 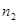соответствует трудоёмкости вычисления матрицы вторых производных; при использовании численного дифференцирования . Квадратичный рост потерь на поиск с увеличением размерности – главный недостаток метода Ньютона (метода второго порядка), не получившего по этой причине широкого распространения.

Количество шагов зависит от многих факторов, часть которых не удаётся выявить и оценить заранее и определяется, в основном, ресурсами машинного времени.

3.2 Адаптация поисковых алгоритмов и вопросы эффективности

При решении конкретных задач оптимального проектирования обычно ориентируются на некоторые математические свойства критерия оптимальности , которые характерны для рассматриваемого класса задач оптимизации (выпуклость, нелинейность, унимодальность, количество локальных экстремумов и т.д.). Тем самым выделяется класс функций, обладающих одними и теми же фиксированными свойствами, а также соответствующий класс алгоритмов, в которых стратегия поиска определена с точностью до значений параметров. Иными словами, имеющиеся в настоящее время алгоритмы оптимизации ориентированы на применение для достаточно узкого класса функций. Таким образом, отдельные поисковые методы не могут быть рекомендованы в качестве универсальных алгоритмов оптимального проектирования.

Достаточно эффективные алгоритмы оптимального проектирования могут быть построены на основе комбинации различных поисковых методов с целью использования преимуществ отдельных методов.

В соответствии с вышеизложенным актуальными являются разработка алгоритмов оптимизации, учитывающих структуру оптимизируемой функции и изменяющих свои параметры и стратегию поиска (структуру), т.е. адаптационных алгоритмов.

Адаптации параметров поисковых алгоритмов в настоящее время посвящено довольно много работ. Среди них можно отметить работы по

1) адаптации величины рабочего шага[34, 38, 39, 44];

2) адаптации функции распределения направлений рабочего шага [29, 56, 74-77].

Второй тип адаптации - структурный – в настоящее время ещё мало изучен и ему посвящено лишь несколько работ [66, 78-85].

В работе [78] делается первая попытка выбора алгоритма с учётом структуры оптимизируемой функции. При этом сложная структура целевой функции представляется в виде совокупности простых элементов, а для каждого из них используется специально приспособленный алгоритм, имеющий высокую эффективность поиска на данном элементе структуры. Адаптация поискового движения к рельефу поверхности оптимизируемой функции происходит с помощью решающих правил. На тестовых функциях со сложной структурой поверхности была проведена экспериментальная оценка эффективности поиска с помощью предложенного алгоритма.

В работе [79] описываются формирование структуры алгоритмов с использованием различного рода комбинаций операторов типичных для алгоритмов поиска (операторы случайного шага, оценки градиента и т.д.).

В работах [80-82] описывается постановка задачи структурной адаптации алгоритмов. Простейшим путём ее решения в случае конечного множества элементов структур является образование стохастического автомата, переключающего структуры алгоритма. Стохастическая матрица переходов от i -ой структуры к j -ой структуре образуется в процессе поиска в режиме самообучения на основе анализа эффективности работы алгоритмов.

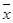В работе [83] рассматривается подход к синтезу алгоритмов поисковой оптимизации, основанный на многомерной линейной экстраполяции. Синтез алгоритма оптимизации предполагает известной информацию I об опыте оптимизации класса оптимизируемых функций в районе точки . Пусть произвольная точка 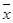характеризуется некоторым вектором ситуации S, компонентами которого служат, например, значение 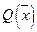, значение ее производных и т.д. Информация о классе решаемых задач представляется в виде выборки, определяющей соответствие между векторами ситуаций и оптимальным решением в этих ситуациях

При поиске решения в произвольной точке 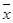, для которой в I не нашлось ситуации S, ситуация, её характеризующая, экстраполируется по ближайшим ситуация обучающей выборки I. Далее, зная экстремум для этой ситуации, определяют оптимальное приращение аргумента в точке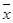

В работе [84] рассмотрены принципы построения многоуровневых адаптивных алгоритмов, позволяющих производить настройку внутренних параметров. К параметрам, которые влияют на точность и скорость поиска авторы относят:

1) величину шага поиска;

2) параметры распределения направления движения;

3) номер координаты, по которой осуществляется движение.

Настройка перечисленных параметров осуществляется в соответствии с определёнными условиями локального улучшения. Разработана программа выбора алгоритма стохастической оптимизации.

В работе [85] делается попытка обобщить и расширить подход к структурной адаптации алгоритмов. Система, описанная в [85] является первой работающей системой поисковой оптимизации, реализующей принцип структурной адаптации.

Автор [66] рассматривает методы решения задач в случаях, когда нет априорной информации для выбора алгоритмов, приводящей к вопросам параметрической и структурной адаптации. Рассмотренный в статье пример подчеркивает необходимость использования принципов структурной адаптации и указывает на возможность создания надёжных систем решения экстремальных задач из ненадёжных алгоритмов.

Высокая интенсивность появления задач оптимизации, разнообразие и сложность реальных объектов проектирования вынуждает обратиться к адаптивному подходу [78, 85].

Идея такого подхода заключается в следующем. В некоторой локальной области независимых переменных 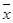функция качества идентифицируется системой признаков, зависящих от «рельефа» , числа «удачных» и «неудачных» шагов поиска, наличие ограничений, размерности гиперпространства и т.д. На основе системы признаков на локальном участке относится к некоторому классу, для которого выявляется эффективный алгоритм поиска. Адаптивный выбор алгоритма связан с построением так называемой «решающей функции» [85], которая в процессе функционирования указывает, какой алгоритм должен быть выбран на следующем этапе поиска.

Задача повышения эффективности решения оптимизационных задач на основе структурной адаптации поисковых алгоритмов требует проведения следующих исследований:

3) На основе анализа топологии поверхностей отклика реальных объектов оптимизации оценить пространство поисковых ситуаций ;

4) Для каждой из выделенных ситуаций разработать критерии её распознавания;

5) На основе теоретических и экспериментальных исследований существующих алгоритмов оптимизации, определить конечное их множество , предназначенных для решения задач оптимального проектирования с учётом пространства поисковых ситуаций ;

6) На основе анализа эффективности каждого алгоритма из множества , определить допустимую область его применения;

7) Построить решающие функции выбора для каждой поисковой ситуации из выделённого множества определённого алгоритма оптимизации;

В настоящей работе описана методика использования алгоритмов оптимизации, основанная на адаптивном принципе, позволяющем гибко применять к широкому классу функций ряд алгоритмов оптимизации.

Принцип адаптивной оптимизации, заключающийся в адаптации процесса поиска (изменение параметров алгоритма, вектора направления поиска, смена алгоритма и т.д.) к характеру изменения оптимизируемой функции, осуществляется на двух уровнях – внешнем и внутреннем.

Внешний уровень включает выбор последовательности методов, основанный на информации о характере самого метода при решении различных тестовых и конкретных задач.

Внутренний уровень включает выбор последовательности методов и изменение их параметров на основе информации, получаемой в процессе решения конкретной задачи.

В последующих разделах рассматриваются вопросы выбора методов оптимизации, относящиеся к вышеописанным уровням и использующих информацию, накопленную в процессе поиска.

3.3. Определение множества поисковых ситуаций и

разработка критериев их распознавания

На основе рассмотрения множества задач оптимизации могут быть выделены следующие характерные поисковые ситуации [8, 78, 85 ]:

5) размерность гиперпространства ;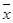

6) крутой спуск (подъём);

7) площадка;

8) окрестность экстремума;

9) овраг;

10) многоэкстремальность;

11) сложность объекта оптимизации.

Вышеуказанные ситуации достаточно полно описывают возможные элементы структуры оптимизируемой функции. Для каждой из ситуации на основе критерия распознавания, характеризуемого системой признаков, формируется соответствующий элемент множества , принимающий в зависимости от выполнения некоторых условий значения 0 или 1 и характеризующий данную поисковую ситуацию.

Ситуация 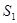(размерность гиперпространства )

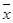В работах [15, 20, 25 ] приведены рекомендации относительно применения поисковых алгоритмов в зависимости от размерности гиперпространства. Большинство работ посвящено оценкам применения регулярных и случайных алгоритмов в указанной ситуации.

В общем случае, для каждого поискового алгоритма предельная размерность гиперпространства будет своя и определение значения её для каждого алгоритма должно производиться экспериментальным путём.

В данной работе автор основываясь на рекомендациях, приведённых в вышеуказанных работах, принимает оценку значения равную 10.

Ситуация (крутой спуск или подъём)

Ситуация соответствует область , в которой удовлетворяется условие

(3.1)

где - множество индексов;

- критическая крутизна гиперповерхности .

При выполнении условия (3.1) .

Ситуация (площадка)

Ситуация характеризуется незначительным изменением при сравнительно большом изменении . Таким образом, критерий распознавания ситуации определяется следующей системой неравенств

;

- некоторый коэффициент;

- коэффициент, характеризующий размер площадки;

- модуль приращения аргументов в гиперсфере 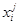с увеличивающимся радиусом, причём точки выбираются на ней случайным образом.

Ситуация 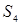(окрестность экстремума)

Близость к области экстремума определяется условием

(3.2)

Если выполняется условие (3.2), то есть основание предполагать, что экстремум расположен в окрестности . Далее, выбирая случайным образом m точек , принадлежащих окрестности проверяем условие

(3.3)

Причём, количество экспериментов m по методу Монте-Карло в области экстремума должно удовлетворять неравенству

,

где q – некоторый коэффициент.

При выполнении условий (3.2) и (3.3) формируется признак идентификации ситуации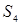

Ситуация (овраг)

Наиболее трудной ситуацией с точки зрения эффективности поиска является ситуация «овраг», что соответственно приводит к сложному и трудоёмкому критерию распознавания ситуации.

Не нашли, что искали? Воспользуйтесь поиском: