Выбор независимых переменных 9 страница. Поставленная задача сводится к минимизации функции

Поставленная задача сводится к минимизации функции

при ограничениях

Для расчёта коэффициентов зависимостей (5.5) используется дробный факторный эксперимент типа ДФЭ с генерирующим соотношением . Интервалы варьирования параметров представлены в таблице 5.12 Коэффициенты аппроксимирующих выражений представлены в таблице 5.13.

Для преобразования исходной задачи на условный экстремум к задаче безусловной минимизации используется метод штрафных функций. В соответствии с этим методом находят последовательность точек вспомогательной функции

(5.6)

где

при последовательном увеличении коэффициента штрафа 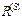. При этом 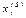стремится к искомому решению .

Результаты поиска оптимальных параметров АД из условия минимального времени пуска приведены в таблицах 5.14 и 5.15. Максимальный и установившийся токи статора по условиям задачи не должны превышать 227А и 25А, т.е. тех значений, которые имеет двигатель при номинальных параметрах.

Варьируемые параметры асинхроннго двигателя

Таблица 5.12

Факторы	Параметры асинхронной машины	Уровни факторов	Интервал варьирования
нижний -1	верхний +1	нулевой 0
	- активное сопротивление статора, Ом	0.045	0.075	0.060	0.015
	- активное сопротивление ротора, Ом	0.090	0.150	0.120	0.030
	- инд. сопротивление реакции статора, Гн	3.60	6.00	4.80	1.20
	- инд. сопротивление рассеяния статора, Гн	0.18	0.30	0.24	0.06
	- момент инерции ротора,	0.003	0.0074	0.0052	0.0022

Коэффициенты полиномиальных моделей

Таблица 5.13

Функции отклика	Коэффициенты полиномов
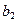
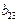
	226.9	-2.30	-9.47	-1.83	-22.97	1.28	-0.03	1.27	0.57	-0.43	-0.5	3.36	1.76	0.53	0.02	-1.07
	25.18	-0.001		-6.0	-0.34			0.001	0.001				-0.001	0.15
	0.174	0.0037	-0.015	0.0025	0.026	0.071	0.0001	-0.0025	0.0012	0.0012	0.0012	-0.005	-0.005	-0.0001	0.0001	0.0112

Таблица 5.16

Критерий оптимизации	Значения ограничений	Значения критерия оптимизации и ограничений в точке оптимума	Координаты точки оптимума	Параметры объекта	Результаты расчёта переходных процессов объекта
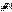
			+1.0000 +1.0000 +0.9945 -0.8931 -1.0000
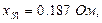
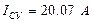
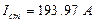
			+1.0000 +1.0000 +1.0000 +1.0000 -1.0000

Результаты расчётов, приведенные в таблице 5.14, показывают, что при заданной точности:

- наилучшее приближение к искомому решению дают методы случайного поиска, Гаусса-Зейделя, квадратичной аппроксимации;

- наименьшее число обращений к минимизируемой функции имеют методы Гаусса-Зейделя и наискорейшего спуска;

- наибольшее число обращений к минимизируемой функции имеют методы случайного поиска и квадратичной аппроксимации.

Результаты решения задачи при уменьшении точности поиска (табл. 5.15) позволяют к вышеуказанному добавить, что наилучшее приближение к искомому решению также имеет метод Гаусса-Зейделя, который имеет наименьшее число обращений к минимизируемой функции.

Аналогичным образом решается задача параметрического синтеза АД с точки зрения min при сохранении в прежних пределах времени пуска и установившегося значения тока статора. Параметры объекта, полученные в результате решения обеих задач оптимизации, приведены в табл.5.16.

Результаты решения задач оптимизации показывают, что варьируя параметры объекта (АД), можно добиться уменьшения времени пуска с до , а также снижения величины с 227А до 193,3А при сохранении в прежних пределах других показателей динамики.

В целях проверки достоверности полученных результатов, были рассчитаны переходные процессы запуска асинхронной машины от сети переменного тока напряжением U=120В и частотой f=400 Гц с использованием системы уравнений [88] и параметров (табл. 5.16). Расчеты показывают хорошее совпадение результатов вычислений по полиномиальной модели с результатами, полученными решением системы алгебро-дифференциальных уравнений объекта.

5.2.2 Оптимальное проектирование синхронного генератора (СГ)

Решение задачи оптимизации СГ по критерию качества переходных процессов позволяет [89]:

- наряду с применением оптимальных регуляторов оценить улучшение динамики АСЭ за счёт изменения параметров объекта регулирования;

- более обоснованно подходить к вопросам конструирования синхронных машин.

Исследовалась возможность улучшения качества переходных процессов в АСЭ с электромеханическим приводом постоянной скорости. Динамические свойства системы оценивались с помощью интегральной квадратичной оценки

где , - отклонения напряжения и частоты в АСЭ от установившихся значений;

, - весовые коэффициенты.

В качестве расчётных в АСЭ были выбраны режимы включения статической нагрузки номинальной мощности. Оптимизируемыми параметрами синхронной машины являлись:

- активное сопротивление и индуктивность рассеяния статорной обмотки;

- активное сопротивление обмотки возбуждения;

- индуктивность реакции статора по продольной оси;

- индуктивность статорной обмотки по поперечной оси.

Интервал изменения оптимизируемых параметров составляет от номинальных значений.

Для оптимизации используются следующие методы НЛП:

1) метод случайного поиска с адаптацией шага [34];

2) метод Келли - Уиллинга, содержащий элементы адаптации и самообучения [4];

3) метод наискорейшего спуска [41].

В таблице 5.17 приведены результаты поиска минимума критерия оптимальности методом [34]: за 100 шагов удалось на порядок снизить показатель качества . Переходные процессы режима наброса номинальной нагрузки до оптимизации (штриховые линии) и после оптимизации (сплошные линии) приведены на рис. 5.4.

Исследование проводилось при оптимальных регуляторах напряжения и частоты [13].

Регуляторы представлены в математическом описании АСЭ уравнениями

Где , - уставки регуляторов,

- отклонение тока в линии постоянного тока [10].

Как видно из сравнения кривых, путём изменения параметров СГ удалось добиться снижения колебательности процесса по координатам U, f. Некоторые параметры СГ в результате оптимизации достигли нижних границ области ().

Далее были проведены расчёты с использованием метода Келли-Уиллинга [4].

Результаты поиска представлены в таблице 5.18, переходные процессы на рис. 5.5. За 148 шагов поиска значение критерия качества уменьшилось почти в 3 раза. Причина отклонения частоты от уровня 400 Гц после оптимизации (рис. 5.5) связана со значениями весовых коэффициентов (). За счёт увеличения можно было добиться улучшения качества процесса по частоте.

В следующей серии вычислительных экспериментов оптимизация была осуществлена с использованием детерминированного метода НЛП - метода наискорейшего спуска [41]. Как и ранее, исследование проводилось для режима включения статической нагрузки при оптимальных регуляторах напряжения и частоты. При этом постоянная времени обмотки возбуждения была постоянной.

В качестве оптимизируемых параметров СГ были выбраны , , , , ,

Результаты поиска приведены в таблице 5.19, кривые переходных процессов - на рис. 5.6.

Результаты проведённых исследований свидетельствуют о том, что для улучшения качества переходных процессов в АСЭ при варьировании параметров объекта регулирования необходимо уменьшать параметры СГ (причём, такие как , в большей степени, чем , ).

Сравнительный анализ численных методов оптимизации демонстрирует достоинство метода наискорейшего спуска, заключающееся в значительном снижении функции качества за приемлемое количество шагов.

В целом результаты проделанной работы свидетельствуют о перспективности применения методов нелинейного программирования для оптимального проектирования электрических машин автономных электроэнергетических систем.

Результаты оптимизации параметров СГ из условий minQ в режиме наброса нагрузки (оптимальный регулятор)

Оптимизация параметров СГ в АСЭ с эл. мех. ППС при набросе нагрузки

(метод случайного поиска)

Таблица 5.17

Число шагов N	Показатель качества Q
	0.168						2.36
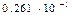
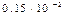
							2.36
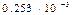
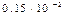
							2.29
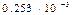
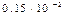
							2.13
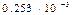
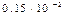
							2.13
							2.13
							2.13
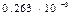
							2.13
							2.13
							2.13
							2.13
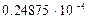
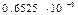
Ограничения на параметры СГ	Верхние						2.95
Нижние						1.77

Таблица 5.18

Оптимизация параметров СГ в АСЭ с эл.мех. ППС

при набросе нагрузки (метод Келли-Уиллинга)

Число удач. шагов Nуд	Общее число шагов N	Функ ция качества Q
Ом	Ом	Гн	Гн	-	Ом
		0,5090	0,1998	0,3024	0,2729	0,5189	0,5448	0,2354
		0,4885	0,2	0,307	0,268	0,521	0,55	0,1834
		0,4576	0,1996	0,302	0,264	0,529	0,554	0,1856
		0,4391	0,2	0,306	0,258	0,54	0,567	0,183
		0,406	0,201	0,303	0,253	0,547	0,567	0,188
		0,4045	0,202	0,3065	0,251	0,546	0,574	0,189
		0,39	0,198	0,309	0,253	0,543	0,571	0,193
		0,37	0,195	0,31	0,25	0,54	0,575	0,196
		0,36	0,193	0,309	0,248	0,546	0,576	0,197
		0,31	0,1988	0,263	0,227	0,544	0,477	0,177
		0,3	0,1989	0,268	0,231	0,554	0,46	0,186
		0,25	0,194	0,236	0,23	0,53	0,424	0,19
		0,215	0,198	0,225	0,206	0,527	0,425	0,184
		0,187	0,185	0,225	0,206	0,549	0,4	0,191
		0,186	0,177	0,225	0,215	0,54	0,4	0,202
		0,164	0,156	0,254	0,207	0,98	0,4	0,193
Область поиска	Верхний уровень	0,2488	0,375	0,344	0,6525	0,68	0,295
Нижний уровень	0,1493	0,225	0,206	0,39	0,4	0,177

Не нашли, что искали? Воспользуйтесь поиском: