Линейные пространства над конечными полями

Конечное поле, состоящее из n элементов, мы будем обозначать F_n.

По поводу конечных полей мы будем предполагать известными следующие факты:

1) для любого n = p^m, где p — простое число, существует единственное (с точностью до изоморфизма) поле из n элементов;

2) поле из n элементов существует только в том случае, когда n = p^m, где p — простое число.

Для поля из n = p^m элементов, где p — простое число, это число p называют характеристикой.

Линейные пространства над конечными полями определяются точно так же, как линейные пространства над R или над C, но у них, конечно, есть некоторые специфические свойства.

Прежде всего, отметим, что линейное пространство размерности k над полем F _n состоит из n^k векторов. Действительно, любой вектор этого пространства имеет вид (x ₁,..., x_k), где каждая из координат xi принимает любое из n возможных значений.

Если поле F_n содержит F_m в качестве подполя, то F_n является линейным пространством над F_m некоторой размерности k, поэтому n = mk.

В частности, поле F₈ не содержит подполя F₄. И вообще, если поле F _pⁿ содержит подполе F _p^m, то n = m^k для некоторого натурального числа k.

Метрика Хемминга

Начать стоит с определения Эвклидова пространства.

Эвклидово пространство – пространство арифметическое над полем действительных чисел. Бесконечное, мать его.

Там есть скалярное произведение. Свойства его таковы:

1. (a, b) = (b, a)

2. (a + g, b) = (a, b) + (g, b)

3. (aR,b) = R(a,b)

4. (a,a) >= 0 (не выполняется в GF(2)); a=0 => (a,a)=0

Вообще, мы считаем скалярным произведением – длину одного вектора помноженную на длину другого и cos угла между ними. Но есть другой способ:

A = (a₁, a₂, …, a_n)

B = (b₁, b₂, …, b_n)

Норма (длина) вектора: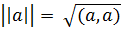

Расстояние между векторами ρ(a,b) = ||a-b||

Свойства:

1. ρ(a,b) > 0 a≠b (a=b => ρ=0)

2. ρ(a,b) = ρ(b,a)

3. ρ(a,b) <= ρ(a,g) + ρ(g,b) (неравенство треугольника)

Все они выполняются для GF(2) и называются Метрикой Хэмминга.

Метрика (длина) вектора – количество не совпавших его компонентов.

Метрика Хэмминга – число не совпавших элементов в векторах.

Свойства этой метрики:

1. ||a|| > 0, a ≠ 0

2. ||a,r|| = ||a||

3. ||a + b|| <= ||a||+||b||

Не нашли, что искали? Воспользуйтесь поиском: