Тригонометрическая форма записи комплексного числа.

Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е. 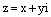и полярные , то они связаны соотношением (1):

.

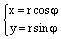По определению, и из (1) получаем:

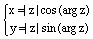. (9)

Подставляя в алгебраическую форму записи числа z получаем: 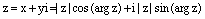. Или

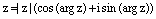(10)

Определение. Запись комплексного числа в виде (3) называется его тригонометрической формой.

Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:

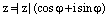, (11)

где .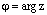

Теорема. (О равенстве комплексных чисел в тригонометрической форме.)

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.

Доказательство. Так как между всеми комплексными числами и всеми точками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.

Теорема доказана.

Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.

Пусть 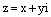, т.е. 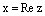, . Тогда

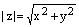, (12)

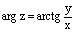, если точка z лежит в первой или четвертой четверти или , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где .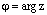

7)

Интеграл типа Коши

Выражение

,

где 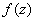- аналитическая функция на замкнутой области 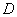, ограниченной положительно ориентированным контуром , называется интегралом Коши.

2.1)

Не нашли, что искали? Воспользуйтесь поиском: