Сходимость числовых положительных рядов Необходимый признак сходимости ряда. Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость

Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. При этом возможны два случая:

1) Ряд 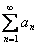расходится. Это значит, что бесконечная сумма равна бесконечности: . Хороший пример расходящегося числового ряда встретился в начале урока: 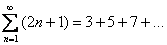. Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому 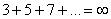и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.

2) Ряд 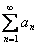сходится. Это значит, что бесконечная сумма равна некоторому конечному числу : 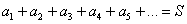. В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы: 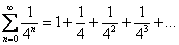. Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формул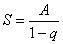е: , где – первый член прогрессии, 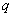– основание прогрессии. В данном случае: 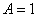, 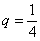. Таким образом: 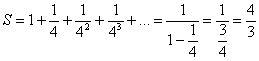. Получено конечное число, значит, ряд сходится, что и требовалось доказать.

На практике в подавляющем большинстве примеров сумму ряда находить не требуется. Для установления сходимости (расходимости) ряда мы не будем пытаться найти сумму ряда. Для этого используются специальные признаки, которые доказаны теоретически.

Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда 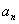, образно говоря – от «начинки» ряда. На этом уроке мы рассмотрим необходимый признак сходимости ряда и признаки сравнения.

! Для дальнейшего усвоения урока необходимо хорошо понимать, что такое предел и хорошо уметь раскрывать неопределенность вида . Для повторения материала обратитесь к статье Пределы. Примеры решений.

Не нашли, что искали? Воспользуйтесь поиском: