
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Связанные определения
- В случае, если
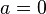 , этот ряд также называется рядом Макло́рена.
, этот ряд также называется рядом Макло́рена.
Свойства
- Если
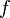 есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке
есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке  области определения
области определения 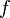 сходится к
сходится к 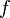 в некоторой окрестности
в некоторой окрестности  .
. - Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности
 . Например, Коши предложил такой пример:
. Например, Коши предложил такой пример:

У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке 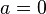 равны нулю.
равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
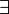 точка точка 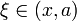 при при 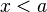 или или 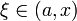 при при 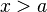 : :

|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Не нашли, что искали? Воспользуйтесь поиском:
 имеет
имеет 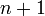 производную в некоторой окрестности точки
производную в некоторой окрестности точки 

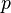 — произвольное положительное число,
— произвольное положительное число,