
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Если общий член ряда не стремится к нулю, то ряд расходится
Или короче: Если 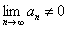 , то ряд расходится.
, то ряд расходится.
В качестве «динамической» переменной вместо «икса» у нас выступает 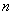 . Букву можно заменить другой буквой, и это не страшно, однако есть разница с содержательной точки зрения. Пределы с «иксом» называют пределами функций, а пределы с переменной «эн» называют пределами числовых последовательностей. Очевидное отличие состоит в том, что переменная «эн» принимает дискретные (прерывные) натуральные значения: 1, 2, 3 и т.д. Но данный факт мало сказывается на методах решения пределов и способах раскрытия неопределенностей.
. Букву можно заменить другой буквой, и это не страшно, однако есть разница с содержательной точки зрения. Пределы с «иксом» называют пределами функций, а пределы с переменной «эн» называют пределами числовых последовательностей. Очевидное отличие состоит в том, что переменная «эн» принимает дискретные (прерывные) натуральные значения: 1, 2, 3 и т.д. Но данный факт мало сказывается на методах решения пределов и способах раскрытия неопределенностей.
Докажем, что ряд из первого примера 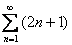 расходится.
расходится.
Общий член ряда: 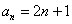
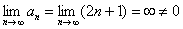
Вывод: ряд 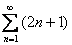 расходится, так как не выполнен необходимый признак сходимости ряда.
расходится, так как не выполнен необходимый признак сходимости ряда.
Необходимый признак сходимости ряда довольно часто встречается в практических заданиях:
3.2)
|
3.3)
Признак Д’Аламбера
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
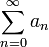
существует такое число 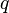 ,
, 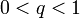 , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство
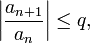
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
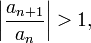
то ряд расходится.
Не нашли, что искали? Воспользуйтесь поиском:
 и
и 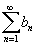 − такие, что
− такие, что 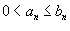 для всех n. Тогда справедливы следующие признаки:
· Если
для всех n. Тогда справедливы следующие признаки:
· Если 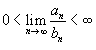 , то оба ряда
, то оба ряда 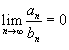 , то ряд
, то ряд  , то ряд
, то ряд  сходится при p > 1 и расходится при 0 < p ≤ 1.
сходится при p > 1 и расходится при 0 < p ≤ 1.