Определители 2 и 3 порядка. Решение систем линейных уравнений по формулам Крамера. Основные случаи решений системы линейных уравнений.

Решением системы называется пара чисел, которая обращает каждое уравнение системы в верное равенство.

Способы решения:

Подстановка

Сложение

Графически

По формулам Крамера

Формулы Крамера применяются для решений систем линейных уравнений.

Определителем 2го порядка составленного из чисел a₁, a₂,b₁,b₂, называется число вида: ∆=| a₁ b₁|

|a₂ b₂|

= a₁ b₂- a₂ b₁

∆_х=|с₁ b₁|= с₁ b_2- с₂ b₁

| с₂ b₂|

∆_у=| a₁ с₁|= a₁ с_2- a₂ с₁

|a₂ с₂|

∆_{х у}- вспомогательный определитель

Если ∆≠0, то х=∆_х/∆

Если ∆=0, то либо система не имеет решений, либо имеет бесконечное множество решений.

Если ∆=0, а ∆_{х и} ∆_у ≠ 0, то система не имеет решений.

Определители 3го порядка:

∆=| a₁ b₁ с₁|= a₁ b₂ с_3- a₂ b₁ с_3- b₃ с₂ a_{1 +} a₃ b₂ с₁₊ a₂ b₃ с₁₊ b₁ с₂ a₃

| a₂ b₂ с₂|

| a₃ b₃ с₃|

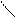
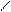
х=∆_х/∆=|d₁ b₁ c₁|

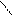
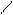|d₂ b₂ c₂|: ∆ - - + + +

|d₃ b₃ c₃|

у=∆_у/∆=|a₁ d₁ c₁|

|a₂ d₂ c₂|: ∆

|a₃ d₃ c₃|

z=∆_z/∆=|a₁ b₁ d₁|

|a₂ b₂ d₂|: ∆

|a₃ b₃ d₃|

Не нашли, что искали? Воспользуйтесь поиском: