Параллельное проектирование. Свойства параллельных проекций. Изображение фигур в стереометрии.

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a, b, с одни и те же для всех точек (x; y; z).
Параллельный перенос в пространстве обладает следующими свойствами:
1. Параллельный перенос есть движение.
2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя.
4. Каковы бы ни были точки A и A`, существует единственный параллельный перенос, при котором точка A переходит в точку A`.
5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

В стереометрии изучаются свойства фигур в пространстве (т.е. свойства пространственных фигур).

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников (рис. 1–10). Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми (рис. 1) и невыпуклыми (рис. 2).

Приведем примеры отдельных многогранников.

Куб представляет собой многогранник, у которого шесть граней, и все они — равные квадраты. У куба 12 равных ребер и 8 вершин (рис. 3).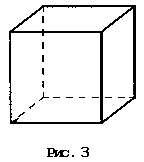

Параллелепипед представляет собой многогранник, у которого шесть граней, и каждая из них — параллелограмм. Параллелепипед может быть прямым (рис. 4) или наклонным (рис. 5).

Параллелепипед, все грани которого прямоугольники, называют прямоугольным. Прямоугольный параллелепипед изображается также, как и прямой. Из сказанного следует, что куб — это прямоугольный параллелепипед с равными ребрами.

n-угольная пирамида представляет собой многогранник, одна грань которого, называемая основанием пирамиды, — некоторый выпуклый n-угольник, а остальные n граней — треугольники с общей вершиной (рис. 6). Эта общая вершина называется вершиной пирамиды, а треугольники — боковыми гранями пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами ее основания, называются боковыми ребрами пирамиды. Пирамида, в основании которой лежит правильный n-угольник, а боковые ребра равны между собой, называется правильной пирамидой (рис. 7). Пирамида, в основании которой лежит треугольник, называется треугольной пирамидой или тетраэдром. Таким образом, тетраэдр —

это четырехгранник. Все его четыре грани — треугольники. Тетраэдр, все четыре грани которого — равные правильные треугольники, называется правильным тетраэдром (рис. 8). Правильный тетраэдр — это частный случай правильной треугольной пирамиды.

n-угольная призма представляет собой многогранник, две грани которого, называемые основаниями призмы, — равные n-угольники, а все остальные n граней — параллелограммы. Они называются боковыми гранями призмы. Призма может быть прямой (рис. 9) или наклонной (рис. 10). У прямой призмы все боковые грани — прямоугольники, у наклонной призмы хотя бы одна грань — параллелограмм, не являющийся прямоугольником.

Параллелепипед — это призма, в основании которой лежит параллелограмм.

Не нашли, что искали? Воспользуйтесь поиском: