Параллельность и перпендикулярность прямых, заданных уравнениями. Условием параллельности двух прямых, заданных уравнением

Условием параллельности двух прямых, заданных уравнением

у=k₁x+b₁ (1)

y=k₂x+b₂ (2)

служит равенство двух коэффициентов

а₁=а₂,

т. е. прямые (1) и (2) параллельны, если угловые коэффициенты равны, и не параллельны, если угловые коэффициенты не равны.

Пример. Прямые y=3x-5 и y=3x+4 параллельны, так как у них угловые коэффициенты равны (k₁=k₂=3)

Замечание 1. Если уравнение одной из двух прямых не содержит ординаты (т.е. прямая параллельна оси ОY), то она параллельна другой прямой при условии, что уравнение последней также не содержит у. Например, прямые 2х+3=0 и х=5 параллельны, а прямыех-3=0 и х-у=0 не параллельны.

Замечание 2. Если две прямые представлены уравнениями

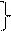А₁х+В₁у+С₁=0

А₂х+В₂у+С₂=0

то условие их параллельности есть

А₁В₁-А₂В₂=0

или в другом обозначении

А₁ В₁ = 0

А₂ В₂

Пример. Прямые

2х-7у+12=0

х-3,5у+10=0, параллельны, т.к.

2-7 =2.(-3,5)-1.(-7)=0

1-3,5

Условием перпендикулярности двух прямых, заданных уравнениями

у=k₁x+b₁ (1)

y=k₂x+b₂ (2)

служит соотношение

а₁а₂=-1

т.е. две прямые перпендикулярны, если произведение их угловых коэффициентов равно -1, и не перпендикулярны, если оно не равно -1.

Пример. Прямые у=3х и у=-1/3х перпендикулярны, т.к. а1а2=3.(-1/3)=-1

Если две прямые представлены уравнениями

А₁х+В₁у+С₁=0

А₂х+В₂у+С₂=0

то условие их перпендикулярности есть

А₁А₂+В₁В₂=0

Пример. Прямые 2х+5у=8 и 5х-2у=3 перпендикулярны; действительно, здесь А₁=2, А₂=5,В₁=5, В₂=-2,

значит, А₁А₂+В₁В₂=10-10=0

Не нашли, что искали? Воспользуйтесь поиском: