ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Правило дифференцирования суммы двух функций, произведения двух функций, частного двух функций.
Процесс вычисления производной называется дифференци́рованием.
Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х0обозначаются для краткости так: u(х0) = u, v(х0) = v, u'(х0) = u', v'(х0)=v`. Если функции u и v дифференцируемы в точке х0, то их сумма дифференцируема в этой точке и
(u+v)' = u' + v'.
Коротко говорят: производная суммы равна сумме производных.
1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х0+Δx)+ v(х0+Δx) – (u(х0)+v(х0)) = (u(х0+Δx)-u(х0)) + (v(х0+Δx)-v(х0)) = Δu + Δv
3) Функции u и v дифференцируемы в точке х0, т. е. при Δх→0
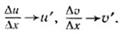
Тогда
при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’
Лемма.. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е.
f(х0 + Δх)→f (х0) при Δx→0
Действительно,
при Δх→0, так как
Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х0 + Δx)→f (х0) при Δх→0.
44. Производная у=х, у=Сх, у=хn
Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции.
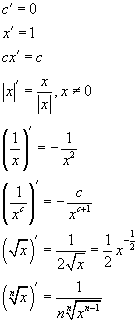1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
2. Производная переменной равна единице
x´ = 1
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|' = x / |x| при условии, что х ≠ 0
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(xc)'= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2)' = 2x
(x3)' = 3x2
6. Производная дроби 1/х
(1/х)' = - 1 / x2
Пример:
(1/x)' = (x-1)', тогда можно применить формулу из правила 5
(x-1)' = -1x-2 = - 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / xc)' = - c / xc+1
Пример:
(1 / x2)' = - 2 / x3
8. Производная переменной под квадратным корнем
(√x)' = 1 / (2√x) или 1/2 х-1/2
Пример:
(√x)' = (х1/2)' значит можно применить формулу из правила 5
(х1/2)' = 1/2 х-1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n√x)' = 1 / (n n√xn-1)
Не нашли, что искали? Воспользуйтесь поиском: