Приращение аргумента и приращение функции. Понятие производной функции. Вычисление производной по 4 действиям.

Свойство функции быть непрерывной в точке равносильно тому, что разность является бесконечно малой при .

Другими словами, это означает, что

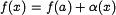
где - бесконечно малая функция при .

Таким образом, для всякой непрерывной функции в точке имеет смысл рассматривать аналитическое выражение (т.е. формулу)

Это выражение называется приращением функции в точке . Оно обозначается так: . Данное обозначение используется и в том случае, когда не является непрерывной функцией в точке

Итак, если при , то функция будет непрерывной в точке , и наоборот. Для простейшей функции ее приращение называется приращением аргумента поскольку при значение функции равно значению аргумента. Это выражение имеет специальное обозначение . Имеем, что при

Аргумент можно выразить через его приращение . Действительно, . Следовательно, при фиксированном приращение можно рассматривать как некоторую функцию от , т.е.

.

Когда хотят подчеркнуть, что значение равно при и , то пишут

или

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.

Не нашли, что искали? Воспользуйтесь поиском: