
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Перпендикулярность прямой и плоскости. Признак препендикулярности прямой и плоскости (доказать).
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Теорема
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной прямой.

Доказательство
Пусть a – прямая, перпендикулярная прямым b и с в плоскости α. Тогда прямая a проходит через точку A пересечения прямых b и с. Докажем, что прямая a перпендикулярна плоскости α.
Проведем произвольную прямую x через точку A в плоскости α и покажем, что она перпендикулярна прямой a. Проведем в плоскости α произвольную прямую, не проходящую через точку A и пересекающую прямые b, с и x. Пусть точками пересечения будут B, C и X..
Отложим на прямой a от точки A в разные стороны равные отрезки AA1 и AA2. Треугольник A1CA2 равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению. Треугольник A1BA2 так же равнобедренный. Следовательно, Δ A1BC = ΔA2BC по третьему признаку равенства треугольников.
Из равенства треугольников A1BC и A2BC следует равенство углов A1BX и A2BX, следовательно, равенство треугольников A1BX и A2BX по первому признаку равенства треугольников. Из равенства сторон A1X и A2X, следует, что A1XA2 равнобедренный. Поэтому его медиана XA является высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости α. Теорема доказана.
35. Двугранный угол. Угол между плоскостям. Трёхгранный угол. Многогранный угол.
 Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Плоскости, образующие двугранный угол, называется его гранями. Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если он равен 90о (меньше 90о, больше 90о)
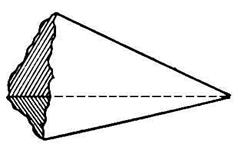 Трехгранный угол – это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трехгранного угла. Стороны углов называются ребрами, плоские углы при вершине трехгранного угла называются его гранями. Грани трехгранного угла образуют двугранные углы.
Трехгранный угол – это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трехгранного угла. Стороны углов называются ребрами, плоские углы при вершине трехгранного угла называются его гранями. Грани трехгранного угла образуют двугранные углы.
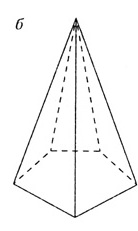
Многогранный угол (a1a2a3... an) определяется как фигура, состоящая из n плоских углов с общей вершиной О.Грани и ребра многогранного угла определяются аналогично граням и ребрам трехгранного угла. Трехгранные углы составляют углы зданий, а многогранные углы — купола отдельных зданий, углы крыш.
Векторы в пространстве. Действия над векторами. Компланарность векторов. Разложение вектора по трем некомпланарным векторам.


 Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором. Направление вектора на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Два вектора равны, если их длины равны и они сонаправлены.
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором. Направление вектора на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Два вектора равны, если их длины равны и они сонаправлены.
 |
b
 c
c
 a
a

 Действие над векторами:
Действие над векторами:
1)Сложение: a+b
Правило треугольника.
 Начало одного вектора совпадает с концом другого.
Начало одного вектора совпадает с концом другого.


 b
b
 |
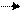 a+b a
a+b a
Правило параллелограмма – общее начало. 

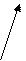



 a+b a
a+b a
 |
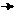

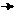
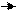 b
b
2)Вычитание: m - n= m +(- n)=…


 Разность двух векторов сводим к нахождению к сумме вектора первого со вторым противоположным второму.
Разность двух векторов сводим к нахождению к сумме вектора первого со вторым противоположным второму.
 |  |  |
m m - n

-n
Умножение вектора на число.
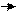
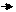
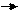




 Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна |k|.| a |, причем векторы a и b сонапрвлены при k > 0 и противоположно направлены при k<0.
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна |k|.| a |, причем векторы a и b сонапрвлены при k > 0 и противоположно направлены при k<0.
 m
m
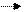 -3 m
-3 m
 2 m
2 m
Векторы называются компланарными, если при откладывании их от одной и ой же точки они будут лежать в одной плоскости.



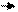



 Если вектор с можно разложить по векторам а и b, т. е. представить в виде с = x a +y b, где х и у – некоторые числа, то векторы a, b и c компланарны.
Если вектор с можно разложить по векторам а и b, т. е. представить в виде с = x a +y b, где х и у – некоторые числа, то векторы a, b и c компланарны.
Если вектор p представлен в виде
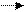
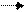
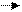
 p=x a +y b +z c,
p=x a +y b +z c,

 где х, у и z-некоторые числа, то говорят, что вектор p разложен по векторам a, b и c.Числа х, у,z называются коэффициентами разложения.
где х, у и z-некоторые числа, то говорят, что вектор p разложен по векторам a, b и c.Числа х, у,z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Не нашли, что искали? Воспользуйтесь поиском: