Ортогональное проектирование. Расстояние от точки до плоскости. Симметрия в пространстве.

Частным случаем параллельного проектирования является ортогональное проектирование. Это параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций.

Пусть даны плоскость α и прямая ℓ, перпендикулярная α. Возьмем произвольную точку пространства А₁, и проведем через неё прямую В₁, параллельную ℓ (соответственно перпендикулярную плоскости α). Прямая ℓ₁ пересечет плоскость α в некоторой точке А. Полученная точка А называется ортогональной проекцией точки А₁ на плоскость α.

Теорема. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции:
S _пр = S cos φ.

Длина перпендикуляра, проведенного из точки А к плоскости α, называется расстоянием от точки А до плоскости

33. Угол между прямой и плоскостью. Теорема о трёх перпендикулярах (доказать)

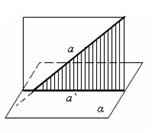
Прямая a пересекает плоскость α. а не перпендикулярна плоскости. Основания перпендикуляров, опущенных из точек прямой a на плоскость α, лежат на прямой a`. Эта прямая называется проекцией прямой a на плоскость α.
Угол между прямой и проекцией этой прямой на плоскость называется углом между прямой и плоскостью.

Теорема. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. Доказательство. Пусть AB – перпендикуляр к плоскости α, AC – наклонная и с – прямая в плоскости α, проходящая через основание С наклонной. Проведем прямую CA` параллельную прямой AB. Она перпендикулярна плоскости α. Проведем через прямые AB и A`C плоскость β. Прямая с перпендикулярна прямой CA`. Если она перпендикулярна прямой CB, то она перпендикулярна плоскости α, а значит, и прямой AC.

Не нашли, что искали? Воспользуйтесь поиском: