
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение логарифмических уравнений и неравенств. Логарифмическим уравнением называется уравнение вида logaf(x)=logag(x), где a>1 и а не равно 1 и уравнения
Логарифмическим уравнением называется уравнение вида logaf(x)=logag(x), где a>1 и а не равно 1 и уравнения, сводящиеся к этому виду.
При их решении обязательно находим ОДЗ или выполняем проверку, т.к..D(loga)=(0;+ бескон), т. е. существуют логарифмы только положительных чисел.
Способы решения:
1.По определению логарифма:
а) простейшее логарифмическое уравнение logax=b, где a>0, a не равно 1 и ab=x
б) более сложные уравнения logaf(x)=b, ОДЗ:f(x)>0 и ab>f(x)
2.Введение новой переменной
3.Разложение на множители
4.Переход к новому основанию
5.Логарифмирование обеих частей уравнения
6.Использование свойств логарифма и получение уравнения logaf(x)=logag(x), где a>0 и а не равно 1
 ОДЗ f(x)>0
ОДЗ f(x)>0
g(x)>0
решение сводится к решению уравнения f(x)=g(x)
это уравнение:
а) надо решить
б) из найденных корней отобрать те, которые удовлетворяют неравенствам f(x)>0;g(x)>0.
Остальные корни уравнения f(x)=g(x) являются посторонними для уравнения logaf(x)=logag(x)
Примеры:
log 2/3x=-3
ОДЗ: x>0
(2/3)-3=x
x=27/8
примеры решения лог. неравенств:
log3x>2
log3x>2.log33
log3x>log332
3>1-функция возрастает
x>9
ОДЗ x>0
Ответ x>0
18.Свойства и график 
Свойства функции 
- D(у) = R;
- нечетная;
- В интервалах (—
 + 2πn;
+ 2πn; 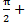 2πn) функция возрастает, а в интервалах (
2πn) функция возрастает, а в интервалах ( 2πn;
2πn;  2πn) она убывает.
2πn) она убывает. - ограничена —1 < у < 1;
- непрерывна;
- E(у) =
 ;
; - Периодическая. С наименьшим периодом 2 π;
- Нули функции sin x=0, при x= πn

19.Свойства и график 
Свойства функции 
- D(у) = R;
- четная;
- В интервалах (— π + 2πn; 2πn) функция возрастает, а в интервалах (2πn; π + 2πn) она убывает.
- ограничена —1 < у < 1;
- непрерывна;
- E(у) =
 ;
; - Периодическая. С наименьшим периодом 2 π;
- Нули функции cos x=0, при x=
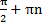

20.Свойства и график y=tgx
Свойства функции y=tgx
- D(у) = R, кроме чисел х=
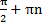
- нечетная;
- Функция возрастает в каждом из промежутков (—
 + πn;
+ πn;  πn)
πn) - неограниченна
- E(у)=R;
- Периодическая. С наименьшим периодом π;
- Нули функции tg x=0, при x=


21.Свойства и график у=ctg x
Свойства функции y=сtg x
Не нашли, что искали? Воспользуйтесь поиском: