Геометрический смысл производной.

Пусть – некоторая кривая, – точка на кривой .

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точке называется предельное положение секущей , если точка стремится к , двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке он имеет невертикальную касательную . Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент k).

По определению углового коэффициента , где – угол наклона прямой к оси .

Пусть – угол наклона секущей к оси , где . Так как – касательная, то при

⇒ ⇒ .

Следовательно, таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

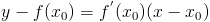
Замечание. Прямая, проходящая через точку перпендикулярно касательной, проведенной к кривой в точке , называется нормалью к кривой в точке . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением , то уравнение нормали к кривой y = f(x) в точке будет иметь вид

, если .

Если же , то касательная к кривой y = f(x) в точке будет иметь вид , а нормаль

Выведем теперь уравнение касательной к графику функции f в точке A (x₀; f(x₀)). Уравнение прямой с угловыми коэффициентом f’(x₀) имеет вид:

y = f’(x₀)*x + b

Для вычисления b воспользуемся тем, что касательная проходит через точку A:

f(x₀) = f’(x₀)*x₀ + b, откуда b = f(x₀)-f’(x₀)*x₀,

значит, уравнение касательной таково:

y=f’(x₀)x-f’(x₀)*x₀+f(x₀), или y=f(x₀)+f’(x₀)(x-x₀).

Не нашли, что искали? Воспользуйтесь поиском: