Нахождение решений уравнений колебания струны методом Эйлера и Даламбера.

По методу Эйлера решаются уравнения вида А = 0, где А,В,С = сonst.

Решение находят в виде u(x,t) = .

Пример. Найти общее решение уравнения А = 0.

Решение. Составляем характеристическое уравнение

Общее решение будет иметь вид u = где

две произвольные функции.

Найти общее решение уравнений методом Эйлера.

1. = 0.

+ 0.

3. = 0.

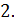
4. = 0.

Решить самостоятельно.

1. = 0.

.

3. = 0.

По методу Даламбера находят решение уравнений свободных колебаний бесконечной струны

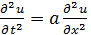, где a .

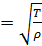с начальными условиями u = f(x),. 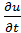= F(x)

t=0 t=0

по формуле

u(x,t) = f(x-at) +f(x+at) + .

Пример. Найти форму струны, определённую уравнением в момент времени t = , если u = sinx; = 1.

t = 0 t = 0

РЕШЕНИЕ. Применим формулу Даламбера x+at

u = sin(x-at) + sin (x+ at) + = sinx cosat + z =

x-at

= sinx cosat +

Ответ: u (x,t) = sin x cos at + t. t = ; u = струна параллельна оси ох.

Найти решение уравнений методом Даламбера

1). ; u = ; = 0.

t = 0 t = 0

2). ; u = 0; = x.

t = 0 t = 0

3).; 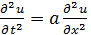; u = 0; = cosx.

t = 0 t = 0

4). Найти форму струны, определяемую уравнением

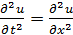, при; u = sinx; = cosx.

t = 0 t = 0

Не нашли, что искали? Воспользуйтесь поиском: