
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение уравнения колебаний струны методом Фурье. Решение уравнений теплопроводности.
Постановка задачи. Найти решение уравнения
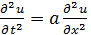 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
u = f(x),. 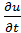 = F(x) и краевым условиям u = 0; u = 0.
= F(x) и краевым условиям u = 0; u = 0.
t=0 t=0 x = 0 x = 
Струна закреплена.
По методу Фурье или методу разделения переменных решение этого уравнения находят в виде
u(x,t) = (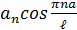 t +
t + 
Функции u (x,t) называются собственными функциями. Коэффициенты 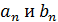 находят, как коэффициенты ряда Фурье по формулам
находят, как коэффициенты ряда Фурье по формулам

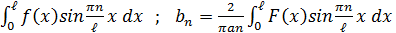 .
.
Окончательная формула имеет вид u(x,t) 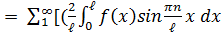 )cos
)cos 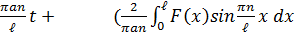 )sin
)sin 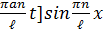 . (1)
. (1)
ЗАДАЧА. Струна длины  закреплена на концах. В начальный момент времени она оттянута в точке x =
закреплена на концах. В начальный момент времени она оттянута в точке x =  на расстояние
на расстояние 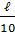 , а затем отпущена без толчка. Методом Фурье определить отклонение u(x,t) точек струны в любой момент времени.
, а затем отпущена без толчка. Методом Фурье определить отклонение u(x,t) точек струны в любой момент времени.
РЕШЕНИЕ. В поставленной задаче имеем дело со свободными колебаниями струны, закреплённой на обоих концах. Её решение сводится к следующей математической задачи.
Требуется определить решение уравнения 
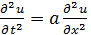 , где a
, где a 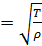 , аТ - натяжение струны,
, аТ - натяжение струны, 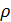 - плотность струны, удовлетворяющее следующим начальным и граничным условиям:
- плотность струны, удовлетворяющее следующим начальным и граничным условиям:
1). Начальные условия
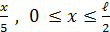 .
.
а). u(x,0) = f(x) =
- 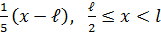 .
.
y
 ……………
……………

 x
x
б). 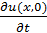 = F (x) = 0 (струна была отпущена без толчка, значит начальная скорость её была равна нулю).
= F (x) = 0 (струна была отпущена без толчка, значит начальная скорость её была равна нулю).
2). Граничные условия: u(0,t) = 0, u(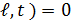 .
.
Физически они означают, что в точках x = 0 и x =  струна закреплена см. рисунок.
струна закреплена см. рисунок.
Согласно методу Фурье, решение находят по формуле (1), вычислив коэффициенты, получим решение
u(x,t) = 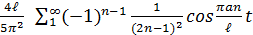 sin
sin  .
.
Не нашли, что искали? Воспользуйтесь поиском: