Решение уравнения Лапласа методом Фурье.

Метод Фурье применяется для решения уравнения Лапласа и задачи Дирихле для простых областей: круг, прямоугольник.

Решим задачу Дирихле для круга радиуса R с центром в начале координат

x² +y² = R² .

Постановка задачи: решить уравнение = 0 при u = f (M_s).

s

РЕШЕНИЕ обычно находят в полярных координатах x = r cos 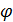; y = r sin 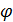, после замены переменных уравнение принимает вид

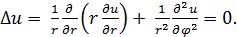Начальные условия: u = u =

r = R

По методу Фурье решение записывается так: u = u (r)Ф(, подставляя в уравнение и, проделав выкладки, получим

u (r, + , где

, n = 1,2,……

ЗАДАЧА 1. На окружности x² +y² R температура распределяется по закону

u = x² – y² + y

x² +y² = R² .

Найти распределение температуры внутри круга, предполагая, что оно стационарно.

Ответ: u(x,y) = x² – y² + ½ y.

ЗАДАЧА 2 Обтекания твёрдого тела потоком идеальной жидкости.

РЕШЕНИЕ. Покажем, что любые установившиеся безвихревые движения идеальной (лишённой вязкости) несжимаемой жидкости также описываются уравнением Лапласа.

Выделим в пространстве, заполненном движущейся жидкостью, произвольный объём D, ограниченный замкнутой поверхностью S.

D

S

V

Пусть V – поле скоростей в потоке жидкости, вектор поля = v₁ i + v₂ j +v₃ k.

Так как поле установившееся и жидкость несжимаемая, то суммарный поток поля через замкнутую поверхность S равен нулю, то есть = 0, где

ds = n⁰ ds. На основании формулы Остроградского имеем

dD = 0, div = .

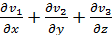Из равенства нулю тройного интеграла следует, что div = 0. С другой стороны – поле безвихревое, следовательно rot = 0, то есть поле потенциальное:

= grad U, где U – потенциал поля.

div(gradU) = 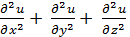= 0 - уравнение Лапласа.

Задачи, связанные с отысканием решений уравнения Лапласа, называют гармоническими задачами.

Не нашли, что искали? Воспользуйтесь поиском: