ФНП. Предел. Непрерывность. Теоремы о непрерывных функциях. Определение частной производной.

Если каждой паре (x, y) значений двух независимых переменных из области D ставится определенное значение z, то говорят, что z есть функция двух переменных (x, y). z=f(x,y). Множество D всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.

U=f(M), D Число b называется пределом функции f(M) при M->M₀, если любое ε>0, то сущ. Окрестность точки М₀ такое, что при любой точке М принадлежащей этой окрестности было справедливо неравенство |f(m)-b|< ε.

Точка М₀ не обязательно принадлежит множеству D, но обязательно должна быть точкой сгущения области D.

Lim f(M)=b, M->M₀

F(M₁),f(M₂),...,f(M_n)

Lim f(M_n)=b, n->∞

По аналогии с функциями одной переменной, вводятся бесконечно малые и большие величины и понятие непрерывности:

Функция называется бесконечно малой при , если

Функция называется бесконечно большой при , если

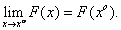Функция называется непрерывной в т. , если Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества.

Функция называется непрерывной в точке M₀, если существует предел функции в точке М, который равен М₀, при М->M₀

Функция задана в этой точке, тогда она не выкалывается.

Теорема 1. Если функция u = f(x) = f(x1, x2, …, xn) непрерывна в точке a, то она непрерывна в этой точке по каждой переменной x1, x2, …, xn.

Обратное утверждение неверно.

Теорема 2. Пусть функции f(x) и g(x), определены в области D М Rn и непрерывны в точке a = (a1, a2, …, an) О D.

Тогда функции f(x) + g(x), f(x) · g(x) и f(x)/g(x) (при g(a) ≠ 0) непрерывны в точке a

Доказательство получается из определения непрерывности функции в точке и теоремы о пределах суммы, произведения и частного двух функций.

Теорема 3. Всякая элементарная функция нескольких переменных непрерывна на множестве, на котором она определена.

Теоремы о свойствах функции одной переменной, непрерывной на отрезке, справедливы для функции нескольких переменных, непрерывной на замкнутом ограниченном множестве (компакте):

Теорема 4. Функция, непрерывная на замкнутом ограниченном множестве, ограничена на этом множестве.

Теорема 5 (Вейерштрасс). Функция, непрерывная на замкнутом ограниченном множестве, достигает на этом множестве своего наибольшего и наименьшего значений.

Рассмотрим функцию u = F (x), определенную в некоторой области D. Пусть − фиксированная точка. Дадим координате х ₁ приращение 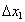. Если существует конечный предел , то он называется частной производной функции F (x) по переменной х ₁ и обозначается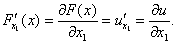

Аналогично определяются частные производные по всем остальным переменным.

Замечания.

1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.

2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.

В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.

Не нашли, что искали? Воспользуйтесь поиском: