ФНП. Полное приращение функции. Его геометрический смысл. Дифференцируемость. Достаточное условие дифференцируемости.

Если каждой паре (x, y) значений двух независимых переменных из области D ставится определенное значение z, то говорят, что z есть функция двух переменных (x, y). z=f(x,y). Множество D всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.

Полным приращением функции в точке называется разность , где и произвольные приращения аргументов. Функция называется дифференцируемой в точке , если в этой точке полное приращение можно представить в виде , где .

Геометрический смысл приращения. Средняя скорость изменения функции

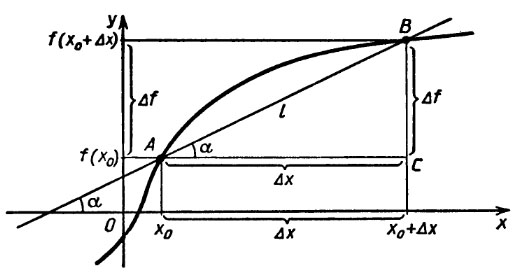
Рассмотрим график функуии y=f(x). Геометрический смысл приращений Δx и Δf (приращение Δf обозначают также Δy) можно понять, посмотрев на рисунок.

Прямую l, проходящую через любые две точки графика функции f, называет секущей к графику f. Угловой коэффициент k секущей, проходящей через точки (x₀; y₀) и (x; y), равен (y-y₀)/(x-x₀). Его удобно выразить через приращения Δx и Δy.

C помощью введеных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀;t₀+Δt]. Если точка движется по прямой и известна ее координата x(t), то

Эта формула верна и для Δt < 0 (для промежутка [t₀+Δt;t₀]). В самом деле, в этом случае перемещение точки равно x(t₀)-x(t₀+Δt); длительность промежутка времени равна - Δt, и, следовательно,

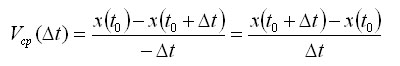
Аналогично выражение

называют средней скоростью изменения функции на промежутке с концами x₀ и x₀+Δx.

Функция называется дифференцируемой в точке , где - область определения функции, если ее полное приращение в этой точке можно представить в виде: , где - числа, которые зависят только от координат точки и не зависят от , а есть бесконечно малая более высокого порядкa, чем бесконечно малая .

Заметим, что согласно определению полное приращение дифференцируемой функции представимо в виде двух частей. Первая часть - является линейной относительно приращений . а вторая - является бесконечно малой более высокого порядка, чем каждое приращение .

В отличие от функции одной переменной для функции многих переменных нельзя дать условие, которое является одновременно необходимым и достаточным условием дифференцируемости.

Теорема 1. (Необходимое условие дифференцируемости).

Если функция переменных дифференцируема в некоторой точке, то она непрерывна в этой точке и имеет в ней конечные частные производные по всем переменным.

Пусть функция дифференцируема в точке из области определения . По определению ее полное приращение можно представить в виде:

Приращения при всех , . Это ясно из того, что - бесконечно малая при , , а поскольку - некоторые числа, то и при , .

2) Если положить , то равенство (1) можно записать в виде или и перейти к пределу при . Тогда , откуда следует, что существует конечный предел . Аналогично можно доказать существование конечных частных производных , ,:., .

Из доказательства теоремы следует, что числа в определении дифференцируемой функции равны значениям частных производных в точке дифференцируемости. Следовательно, полное приращение функции , дифференцируемой в точке , можно представить в виде , где - бесконечно малая более высокого порядка, чем при всех .

Если у функции не существует конечная частная производная хотя бы по одной переменной , то в точке функция не является дифференцируемой.

Теорема 2. (Достаточное условие дифференцируемости).

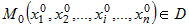Если функция определена на множестве и имеет в точке непрерывные частные производные по всем переменным , то она в этой точке дифференцируема.

рименяя теорему Лагранжа к разностям функций одной переменной, стоящих в скобках, получим

,

Не нашли, что искали? Воспользуйтесь поиском: