ФНП. Дифференциал. Его геометрический смысл. Приложение дифференциала в вычислениях, пример.

Если каждой паре (x, y) значений двух независимых переменных из области D ставится определенное значение z, то говорят, что z есть функция двух переменных (x, y). z=f(x,y). Множество D всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.

Пусть функция y = f (x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная

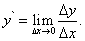
Тогда по определению предела функции разность

(1)

является бесконечно малой величиной при . Выразив из равенства (1) приращение функции, получим

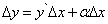(2)

(величина не зависит от , т. е. остаётся постоянной при ).

Если , то в правой части равенства (2) первое слагаемое линейно относительно . Поэтому при

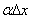оно является бесконечно малой того же порядка малости, что и . Второе слагаемое - бесконечно малая более высокого порядка малости, чем первое, так как их отношение 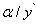стремится к нулю при

Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

(3)

Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают

или

Следовательно,

(4)

или

(5)

Итак, дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет.

Дифференциал функции можно записать в другой форме:

(6)

или

Геометрический смысл дифференциала. Дифференциал функции y = f (x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину .

Пример ; ;

Не нашли, что искали? Воспользуйтесь поиском: