
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Прямая и обратная пропорциональности
Если ¦ - время движения пешехода (в часах), s - пройденный путь (в километрах), и он движется равномерно со скоростью 4 км/ч, то зависимость между этими величинами можно выразить формулой х = 4t. Так как каждому значению t соответствует единственное значение s, то можно говорить о том, что с помощью формулы s =4t задана функция. Ее называют прямой пропорциональностью и определяют следующим образом.
 Определение. Прямой пропорциональностью называется функция, которая может быть задана при помощи формулы у = kх, где k - неравное нулю действительное число.
Определение. Прямой пропорциональностью называется функция, которая может быть задана при помощи формулы у = kх, где k - неравное нулю действительное число.
Название функции у - kх связано с тем, что в формуле у = kх есть переменные х и у, которые могут быть значениями величин. А если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае 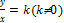 . Это число называют коэффициентом пропорциональности.
. Это число называют коэффициентом пропорциональности.
Функция у = kх является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана выше Другой пример: если в одном пакете муки 2 кг, а куплено х таких пакетов, то всю массу купленной муки (обозначим ее через у) можно представить в виде формулы у = 2х, т.е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k = 2. Напомним некоторые свойства прямой пропорциональности, которые изучаются в школьном курсе математики.
1. Областью определения функции у = kх н областью ее значений является множество действительных чисел.
2. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Поэтому для построения графика прямой пропорциональности достаточно найти лишь одну точку, принадлежащую ему и. не совпадающую с началом координат, а затем через эту точку и начало координат провести прямую.
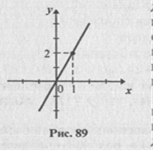 Например, чтобы построить график функции у = 2х, достаточно иметь точку с координатами (1, 2), а затем через нее и начало координат провести прямую (рис. 89).
Например, чтобы построить график функции у = 2х, достаточно иметь точку с координатами (1, 2), а затем через нее и начало координат провести прямую (рис. 89).
3. При k > 0 функция у - kх возрастает на всей области определения; при k < 0 - убывает на всей области определения.
4. Если функция ¦- прямая пропорциональность и {х1, у1), (х2, у2) -пары соответственных значений переменных х и у, причем x2 ¹ 0,
то 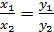 .
.
Действительно, если функция ¦- прямая пропорциональность, то она может быть задана формулой у = kх, и тогда у, = kх1, у2 = kх2. Так как при х 2 ¹ 0 и k ¹ 0, то у2, ¹ 0. Поэтому, 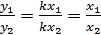 и значит
и значит 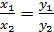 .
.
Если значениями переменных х и у служат положительные действительные числа, то доказанное свойство прямой пропорциональности можно сформулировать так: с увеличением (уменьшением) значения переменной х в несколько раз соответствующее значение переменной у увеличивается (уменьшается) во столько же раз.
Это свойство присуще только прямой пропорциональности, и им можно пользоваться при решении текстовых задач, в которых рассматриваются прямо пропорциональные величины.
Задача 1. За 8 ч токарь изготовил 16 деталей. Сколько часов потребуется токарю на изготовление 48 деталей, если он будет работать с той же производительностью?
Решение. В задаче рассматриваются величины - время работы токаря, количество сделанных им деталей и производительность (т.е.-количество деталей, изготавливаемых токарем за 1 ч), причем последняя величина постоянна, а две другие принимают различные значения. Кроме того, количество сделанных деталей и время работы - величины прямо пропорциональные, так как их отношение равно некоторому числу, не равному нулю, а именно - числу деталей, изготавливаемых токарем за 1 ч. Если количество сделанных деталей обозначить буквой у, время работы х, а производительность - k, то получим, что
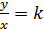 или у = kх, т.е. математической моделью ситуации, представленной в задаче, является прямая пропорциональность. Решить задачу можно двумя арифметическими способами:
или у = kх, т.е. математической моделью ситуации, представленной в задаче, является прямая пропорциональность. Решить задачу можно двумя арифметическими способами:
1 способ: 2 способ:
1) 16:8 = 2 (дет.) 1) 48:16 = 3 (раза)
2) 48:2 = 24(ч) 2) 8×3 = 24 (ч)
Решая задачу первым способом, мы сначала нашли коэффициент пропорциональности k, он равен 2, а затем, зная, что у - 2х, нашли значение х при условии, что у = 48.
При решении задачи вторым способом мы воспользовались свойством прямой пропорциональности: во сколько раз увеличивается количество деталей, сделанных токарем, во столько же раз увеличивается и количество времени на их изготовление.
Перейдем теперь к рассмотрению функции, называемой обратной пропорциональностью.
Если t - время движения пешехода (в часах), u - его скорость (в км/ч) и он прошел 12 км, то зависимость между этими величинами можно выразить формулой u× t = 20 или 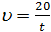 . Так как каждому значению
. Так как каждому значению
t(t ¹ 0) соответствует единственное значение скорости u, то можно говорить о том, что с помощью формулы 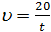 задана функция. Ее называют обратной пропорциональностью и определяют следующим образом.
задана функция. Ее называют обратной пропорциональностью и определяют следующим образом.
Определение. Обратной пропорциональностью называется функция, которая может быть задана при помощи формулы 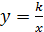 , где k-неравное нулю действительное число.
, где k-неравное нулю действительное число.
 Название данной функции связано с тем, что в
Название данной функции связано с тем, что в 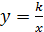 есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности.
есть переменные х и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае ху = k (k ¹ 0). Это число k называют коэффициентом пропорциональности.
Функция 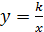 является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики.
является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики.
Одна из них описана перед определением обратной пропорциональности. Другой пример: если купили 12 кг муки и разложили ее в х банок по у кг в каждую, то зависимость между данными величинами можно представить в виде х×у = 12, т.е. она является обратной пропорциональностью с коэффициентом k = 12.
Напомним некоторые свойства обратной пропорциональности, известные из школьного курса математики.
1. Областью определения функции 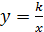 и областью ее значений х является множество действительных чисел, отличных от нуля.
и областью ее значений х является множество действительных чисел, отличных от нуля.
2. Графиком обратной пропорциональности является гипербола.
3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция 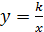 является убывающей на всей области определения х (рис. 90). При k < 0 ветви гиперболы расположены во 2-й и 4-й четвертях и функция
является убывающей на всей области определения х (рис. 90). При k < 0 ветви гиперболы расположены во 2-й и 4-й четвертях и функция 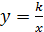 является возрастающей на всей области определениях (рис. 91).
является возрастающей на всей области определениях (рис. 91).

|
4. Если функция ¦- обратная пропорциональность и (х1,у1,), (х2,у2)- пары соответственных значении переменных х и у, то  .
.
Действительно, если функция ¦- обратная пропорциональность, то она может быть задана формулой 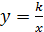 , и тогда
, и тогда  ,
, 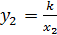 . Так как x1 ¹ 0, х2 ¹ 0 и k ¹ 0, то
. Так как x1 ¹ 0, х2 ¹ 0 и k ¹ 0, то
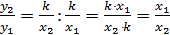 .
.
Если значениями переменных х и у служат положительные действительные числа, то это свойство обратной пропорциональности можно сформулировать так: с увеличением (уменьшением) значения переменной х в несколько раз соответствующее значение переменной у уменьшается (увеличивается) во столько лее раз.
Это свойство присуще только обратной пропорциональности, и им можно пользоваться при решении текстовых задач, в которых рассматриваются обратно пропорциональные величины.
Задача 2. Велосипедист, двигаясь со скоростью 10 км/ч, проехал расстояние от А до В за 6 ч. Сколько времени потратит велосипедист на обратный путь, если будет ехать со скоростью 20 км/ч?
Решение. В задаче рассматриваются величины: скорость движения велосипедиста, время движения и расстояние от А до В, причем последняя величина постоянна, а две другие принимают различные значения. Кроме того, скорость и время движения - величины обратно пропорциональные, так как их произведение равно некоторому числу, а именно пройденному расстоянию. Если время движения велосипедиста обозначить буквой у, скорость - х, а расстояние АВ - k, то получим, что ху = k или 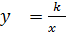 , т.е. математической моделью ситуации, представленной в задаче, является обратная пропорциональность.
, т.е. математической моделью ситуации, представленной в задаче, является обратная пропорциональность.
Решить задачу можно двумя способами:
1 способ: 2 способ:
1) 10-6 = 60 (км) 1) 20:10 = 2 (раза)
2) 60:20 = 3(ч) 2) 6:2 = 3(ч)
Решая задачу первым способом, мы сначала нашли коэффициент пропорциональности k, он равен 60, а затем, зная, что 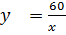 , нашли х значение y при условии, что х = 20.
, нашли х значение y при условии, что х = 20.
При решении задачи вторым способом мы воспользовались свойством обратной пропорциональности: во сколько раз увеличивается скорость движения, во столько же раз уменьшается время на прохождение одного и того же расстояния.
Заметим, что при решении конкретных задач с обратно пропорциональными или прямо пропорциональными величинами накладываются некоторые ограничения на х и у, в частности, они могут рассматриваться не на всем множестве действительных чисел, а на его подмножествах.
Задача 3. Лена купила х карандашей, а Катя в 2 раза больше. Обозначьте число карандашей, купленных Катей, через у, выразите y через х и постройте график установленного соответствия при условии, что х £ 5. Является ли это соответствие функцией? Какова ее область определения и область значений?
 Решение. Катя купила у = 2х карандашей. При построении графика функции у - 2х необходимо учесть, что переменная х обозначает количество карандашей и х £ 5,значит, она может принимать только значения 0, 1, 2, 3, 4, 5. Это и будет область определения данной функции. Чтобы получить область значений данной функции, надо каждое значение х из области определения умножить на 2, т.е. это будет множество {0, 2, 4, 6, 8, 10}. Следовательно, графиком функции у = 2 х с областью определения {0, 1, 2, 3, 4, 5} будет множество точек, изображенных на рисунке 92. Все эти точки принадлежат прямой у = 2х.
Решение. Катя купила у = 2х карандашей. При построении графика функции у - 2х необходимо учесть, что переменная х обозначает количество карандашей и х £ 5,значит, она может принимать только значения 0, 1, 2, 3, 4, 5. Это и будет область определения данной функции. Чтобы получить область значений данной функции, надо каждое значение х из области определения умножить на 2, т.е. это будет множество {0, 2, 4, 6, 8, 10}. Следовательно, графиком функции у = 2 х с областью определения {0, 1, 2, 3, 4, 5} будет множество точек, изображенных на рисунке 92. Все эти точки принадлежат прямой у = 2х.
Упражнения
1. Известно, что функция / является прямой пропорциональностью, задана на множестве X - {1, 2, 3, 4, 5, 6} и при х, равном 3, значение функции равно 12.
а) Задайте функцию ¦ при помощи формулы и таблицы; постройте ее график.
б) Какие свойства функции /можно проиллюстрировать при помощи таблицы и графика?
в) Какие из названных свойств вы будете использовать, решая задачу: «В 3 пакета разложили поровну 12 кг муки. Сколько килограммов муки можно разложить в 6 таких пакетов?»
2. Известно, что функция ¦ является обратной пропорциональностью, задана на множестве X - {1, 2, 3, 5, 6, 10, 15, 30} и при х, равном 5, значение функции ¦ равно 6.
а) Задайте функцию ¦ при помощи формулы и таблицы; постройте ее график.
б) Какие свойства функции ¦ можно проиллюстрировать при помощи таблицы и графика?
в) Какие из названных свойств вы будете использовать, решая задачу: «Муку разложили в 10 пакетов по 3 кг в каждый. Сколько получилось бы пакетов, если бы в каждый положили по 6 кг муки?»
3. Покажите, что зависимость между величинами, о которых идет речь в нижеприведенной задаче, может быть выражена формулой у = kх.
Из 24 м ткани сшили 8 одинаковых платьев. Сколько потребуется ткани на 16 таких же платьев?
4. Учитель, проводя с детьми анализ задачи (см. упр. 3), спрашивает: «Если на 8 платьев израсходовали 24 м ткани, то на 16 платьев израсходуют больше или меньше ткани?» Дети отвечают, что больше, так как 16 больше 8.
О каком свойстве и какой функции в этом случае идет речь?
5. Задайте при помощи формулы соответствие, которое рассматривается в задании:
а) Запиши несколько примеров на деление с результатом 10.
б) Составь все возможные примеры на сложение однозначных чисел с ответом 10.
Установите, являются ли эти соответствия функциями.
6. Одна сторона прямоугольника 3 см, а другая - х см. Какова площадь (у см2) этого прямоугольника? Постройте график полученного соответствия при условии, что х £ 6. Докажите, что это соответствие - функция.
7. Площадь прямоугольника с основанием х см равна 12 см2. Какова высота (у см) этого прямоугольника?
Покажите, что соответствие между значениями переменных х и у является функцией и постройте ее график при условии, что 1 £ х £ 12.
8. Учащимся дано задание заполнить таблицу
| b | ||||||||
| 24:b |
Задает ли эта таблица функцию? Какую? Какое свойство этой функции можно проиллюстрировать при помощи данной таблицы?
9. Обоснуйте, используя определения прямой или обратной пропорциональности и их свойства, решение различными арифметическими способами следующих задач:
а) С участка собрали 6 мешков картофеля по 40 кг в каждом. Этот картофель разложили в ящики по 20 кг в каждый. Сколько ящиков потребовалось?
б) Из куска ткани длиной 24 м сшили 8 одинаковых костюмов. Сколько потребуется ткани на 32 таких же костюма?
10. Какие вспомогательные модели можно использовать на этапе поиска плана решения задач из упражнения 9, если рассматривать их в начальной школе, т.е. при условии, что дети не знают ни прямой, ни обратной пропорциональности?
11. Какие из нижеприведенных задач можно решить в начальной школе двумя способами:
а) Велосипедист ехал со скоростью 12 км/ч и был в пути 2 ч. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 4 км/ч?
б) Из 100 кг свеклы при переработке получается 16 кг сахара.
Сколько килограммов сахара получится из 3 т свеклы?
в) Два опытных участка имеют одинаковую площадь. Ширина первого участка 30 м, ширина второго - 40 м. Найдите длину первого участка, если известно, что длина второго участка равна 75 м.
Не нашли, что искали? Воспользуйтесь поиском: