
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятие соответствия. Способы задания соответствий
Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.
| I. Найти значение выражения: | II. Найти площадь фигуры: | III. Решить уравнение: |
| в1) (17 – 1): 4 |  F1 F1
| y1) 2+x = 6 |
| в2) (12 + 18): (6-6); |  F2 F2
| y2) x – 7 = 4 |
| в3) 2×7+6 |  F3
Рис.66 F3
Рис.66
| y3) 2x = 8 |
В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.
Что общее имеют эти соответствия?
Видим, что во всех случаях мы имеем два множества: в первом - это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором - это множество из трех геометрических фигур и множество N натуральных чисел; в третьем - это множество из трех уравнений и множество N натуральных чисел.
Выполняя предложенные задания, мы устанавливаем связь (соответствие) между этими множествами. Ее можно представить наглядно, при помощи графов (рис. 67).
Можно задать эти соответствия, перечислив все пары элементов, находящихся в заданном соответствии:
I. {(в 1,),(в 3 20)};
II. {(F 1,4), (F 2,10), (F3,10)};
III.{ y1,4), (y2,11), (y3, 4)}.
 |
Полученные множества показывают, что любое соответствие между двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары - это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
 Определение. Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств.
Определение. Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств.
Соответствия принято обозначать буквами Р, S, Т, R и др. Если S-соответствие между элементами множеств X и Y, то, согласно определению, S Ì Х ´ Y.
Выясним теперь, как задают соответствия между двумя множествами. Поскольку соответствие - это подмножество, то его можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества. Так, соответствие между множествами X = {1, 2, 4, 6} и Y = {3, 5} можно задать:
3)при помощи предложения с двумя переменными: а < b при условии, что а Î X, b Î Y ;
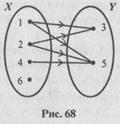
4)перечислив пары чисел, принадлежащих подмножеству декартова произведения Х´Y. {(1, 3), (1,5), (2, 3), (2, 5), (4, 5)}. К этому способу задания относят также задание соответствия при помощи графа (рис. 68) и графика (рис. 69).
 |
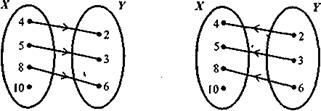
Нередко, изучая соответствие между множествами X и Y, приходится рассматривать и соответствие, ему обратное. Пусть, например, S -соответствие «больше на 2» между множествами X = {4, 5, 8, 10} и Y- {2, 3, 6}. Тогда S = {(4, 2), (5, 3), (8, 6)} и его граф будет таким, как на рисунке 70, а.
Соответствие, обратное данному, - это соответствие «меньше на 2». Оно рассматривается между множествами Y и X, и чтобы его представить наглядно, достаточно на графе соответствия S направление стрелок поменять на противоположное (рис. 70,б). Если соответствие «меньше на 2» обозначить
S-1, то S -1 = {(2,4), (3,5), (6,8)}.
 |
а) б)
Рис. 70
Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: хSу. Запись хSу можно рассматривать как обобщение записей конкретных соответствий: х = 2у; х > 3 у+ 1 и др.
Воспользуемся введенной записью для определения понятия соответствия, обратного данному.
 Определение. Пусть S - соответствие между множествами Х иY. Соответствие S-1 между множествами Y и X называется обратным данному, если у S-1х тогда и только тогда, когда хSу.
Определение. Пусть S - соответствие между множествами Х иY. Соответствие S-1 между множествами Y и X называется обратным данному, если у S-1х тогда и только тогда, когда хSу.
Соответствия S и S называют взаимно обратными. Выясним особенности их графиков.
Построим график соответствия S = {(4, 2), (5, 3), (8, 6)} (рис. 71, а). При построении графика соответствия S -1 = {(2, 4), (3, 5), (6, 8)} мы должны первую компоненту выбирать из множества Y = {2, 3, 6}, а вторую - из множества Х= {4, 5, 8, 10}. В результате график соответствия S -1 совпадет с графиком соответствия S. Чтобы различать графики соответствий S и S -1, условились первую компоненту пары соответствия S -1 считать абсциссой, а вторую - ординатой. Например, если (5, 3) Î S, то (3, 5) Î S -1. Точки с координатами (5, 3) и (3, 5), а в общем случае (х, у) и (у, х) симметричны относительно биссектрисы 1-го и 3-го координатных углов. Следовательно, графики взаимно обратных соответствий S и S-1 симметричны относительно биссектрисы 1-го и 3-го координатных углов.

Чтобы построить график соответствия S-1, достаточно изобразить на координатной плоскости точки, симметричные точкам графика S относительно биссектрисы 1-го и 3-го координатных углов.
Упражнения
5. Вычислив длины заданных отрезков, учащийся записал: АВ - 7 см, СD = 12 см, КL = 15 см, ХY - 12 см. Соответствие между какими множествами он установил? Задайте это соответствие при помощи предложения с двумя переменными и графа.
6. Даны множества: X - {2, 5), Y = {3, 6}. Перечислите элементы декартова произведения данных множеств и образуйте все подмножества полученного множества. Какое из подмножеств задает соответствие: а) «больше»; б) «меньше»; в) «меньше на 1»; г) «меньше в 3 раза»?
 |
3. Соответствие «число х в два раза больше числа у» рассматривается между множествами X и Y. Каким будет его график, если:
а) X = {2,4,6,8}, Y = N; б) Х =[2,8], Y = R;
в) Х=Y= R.
 4. Между множествами X = {0, 1, 2, 3, 4, 5} и Y = Z задано соответствие «х - у = 3», причем х е X, у е Y. Какая фигура на рисунке 72 является графиком этого соответствия?
4. Между множествами X = {0, 1, 2, 3, 4, 5} и Y = Z задано соответствие «х - у = 3», причем х е X, у е Y. Какая фигура на рисунке 72 является графиком этого соответствия?
10. Графиком соответствия Р, заданного между множествами X и Y, являются все точки прямоугольника АВСБ (рис. 73). Назовите координаты трех точек, принадлежащих этому графику и задайте множества Х и Y.
11. Множества X = {1, 3, 4, 6} и Y = {0, 1} находятся в соответствии S = {(1, 1), (3, 0), (3, 1), (4, 0), (4, 1) (6, 1)}. Задайте соответствиеS-1, обратное соответствию Y, и постройте на одном чертеже их графики.
12.  Между множеством X - углов треугольника AВС и множеством Y - его сторон задано соответствие Т - «угол х лежит против стороны у». Задайте соответствие Т-1, обратное соответствию Т, при помощи: а) предложения с двумя переменными; б) графа.
Между множеством X - углов треугольника AВС и множеством Y - его сторон задано соответствие Т - «угол х лежит против стороны у». Задайте соответствие Т-1, обратное соответствию Т, при помощи: а) предложения с двумя переменными; б) графа.
13. Даны графики соответствий Р и Q (рис. 74). Можно ли утверждать, что соответствия Р и Q взаимно обратные?
14. Постройте графики соответствий, обратных данным (рис. 75).
 |
Не нашли, что искали? Воспользуйтесь поиском: