Метод математической индукции. Метод доказательства, который основан на аксиоме 4 (с

Метод доказательства, который основан на аксиоме 4 (с. 254) и который мы использовали при доказательстве свойств сложения и умножения, можно применять и для доказательства других утверждений о натуральных числах. Основой для этого служит следующая теорема.

Теорема 30. Если утверждение А(п) с натуральной переменной п истинно для п = 1 и из того, что оно истинно для п=k(k- произвольное натуральное число), следует, что оно истинно и для следующего числа п = k¹, то утверждение А(п) истинно для любого натурального числа п.

Доказательство. Обозначим через М множество тех и только тех натуральных чисел, для которых утверждение А(п) истинно. Тогда из условия теоремы имеем: 1) 1 Î М; 2) k Î М => k¹ Î М. Отсюда, на основании аксиомы 4, заключаем, что М - N, т.е. утверждение А(п) истинно для любого натурального числа п.

Метод доказательства, основанный на этой теореме, называется методом математической индукции. Состоит оно из двух частей:

1)доказывают, что утверждение A(п) истинно для п = 1, т.е. что истинно высказывание А(1);

2)предполагают, что утверждение А(п) истинно для п =k, и, исходя из этого предположения, доказывают, что утверждение А(п) истинно и п=k+ 1, т.е. что истинно высказывание А (k) => А (k + 1).

Если A (1) Ù А(k) => А(k + 1)- истинное высказывание, то делают вывод о том, что утверждение А(п) истинно для любого натурального числа п.

Доказательство методом математической индукции можно начинать не только с подтверждения истинности утверждения для п = 1, но и с любого натурального числа т. В этом случае утверждение А(п) будет доказано для всех натуральных чисел п ³ т.

Приведем примеры доказательства утверждений методом математической индукции.

Пример 1. Докажем, что для любого натурального числа истинно равенство

1 + 3 + 5 +... + (2 n - 1) = n ².

Равенство 1 + 3 + 5 +... + (2 n - 1) = п² представляет собой формулу, по которой можно находить сумму п первых последовательных нечетных натуральных чисел. Например, 1+3 + 5 + 7 = 4² = 16, 1+3 + 5 +7+ 9 + 11 = 6² = 36; если эта сумма содержит 20 слагаемых указанного вида, то она равна 20² = 400 и т.д. Доказав истинность данного равенства получим возможность находить по формуле сумму любого числа слагаемых указанного вида.

1) Убедимся в истинности данного равенства для п = 1. При п = 1 левая часть равенства состоит из одного члена, равного 1, правая часть равна 1²(т.е. тоже 1). Так как 1 = 1, то для п = 1 данное равенство истинно.

2) Предположим, что данное равенство истинно для п = k, т.е. что1 + 3 + 5 +... +(2 k- 1) = k². Исходя из этого предположения, докажем, что оно истинно и для n=k +1,т.е. 1 + 3 + 5 +... + (2 n - 1) + (2 п +1)=(k +1)².

Рассмотрим левую часть последнего равенства. По предположены сумма первых k слагаемых равна k² и поэтому 1 + 3 + 5 +... + (2 n – 1) + (2 n + 1) = k² + 2k + 1. Выражение k² + 2k + 1 тождественно равно выражению (k + 1)². Следовательно, истинность данного равенств для п = k + 1 доказана.

Таким образом, данное равенство истинно для п = 1 и из истинности его для п = k следует истинность для п = k + 1. Тем самым доказано, что данное равенство истинно для любого натурального числа.

Пример 2. Докажем, что для любого натурального числа истинно утверждение: (8 ⁿ + 6) ⋮7.

1)Убедимся, что данное утверждение истинно для п = 1. Имеем: 8¹ + 6 = 14, но 14 кратно 7. Следовательно, для п = 1 данное утверждение истинно.

2)Предположим, что данное утверждение истинно для п = k, т.е. (8 ^k + 6) ⋮ 7. Исходя из этого предположения, докажем, что оно истинно и для n = k + 1, т.е. (8 ^k+1 + 6)17.

Преобразуем выражение 8 ^k+1 + 6 к виду 8 ^k ×8 + 6. Если к нему прибавить, а затем вычесть произведение 8×6, то получим 8 ^k ×8 + 6 + 8×6-8×6=8×(8 ^k + 6) - 42. В полученном выражении уменьшаемое 8×(8 ^k +6) кратно 7, так как 8 ^k +6 кратно 7 по предположению. Число 42 также делится на 7, следовательно, вся разность кратна 7.

Таким образом, данное утверждение истинно для п = 1 и из истинности его для п = k следует истинность для п=k + 1. Тем самым доказано, что данное равенство истинно для любого натурального числа.

Упражнения

1. Опишите в общем виде процесс доказательства методом математической индукции. Из скольких этапов он состоит?

2. Используя метод математической индукции, докажите, что для любого натурального числа п истинны утверждения:

а) 1²+2²+3²+…+ n²=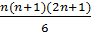

б) 1×2 + 2×3 + 3×4 +...+(n + 1)=

в) 1×4 + 2×7 + 3×10 +... +n (3 n + 1) =n (n + 1) ²;

г) (n ³+ 3 n) ⋮6;

д) (4 ⁿ+ 15 n – 1) ⋮9;

е) (6 ^2n-1+ 1) ⋮7.

Не нашли, что искали? Воспользуйтесь поиском: