
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Скалярное произведение двух векторов. Выражение скалярного произведения через координаты перемножаемых векторов.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение векторов 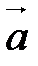 и
и 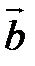 обозначается через (
обозначается через (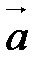 ,
, 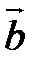 ). Если φ - угол между векторами
). Если φ - угол между векторами 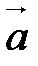 и
и 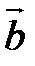 , то (
, то (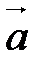 ,
, 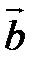 )=
)= 
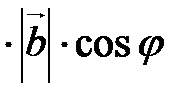 .
.
Скалярное произведение обладает следующими свойствами:
1. (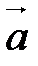 ,
, 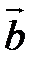 ) =(
) =(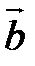 ,
,  ) (коммутативность).
) (коммутативность).
2. ( ,
, 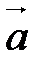 )=
)=  (скалярный квадрат вектора равен квадрату его длины).
(скалярный квадрат вектора равен квадрату его длины).
3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них нулевой.
4. (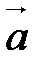 ,
, 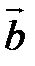 )=
)= 
 =
= 
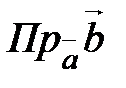 .
.
5. (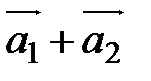 ,
, 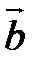 ) = (
) = (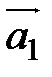 ,
, 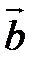 ) + (
) + ( ,
, 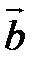 ).
).
6. (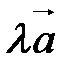 ,
, 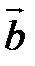 ) +
) + 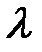 (
(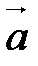 ,
, 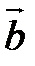 ).
).
Действительно, пусть 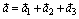 , причем каждое слагаемое коллинеарно соответствующему базисному вектору. Из теоремы второго раздела следует, что
, причем каждое слагаемое коллинеарно соответствующему базисному вектору. Из теоремы второго раздела следует, что  , где выбирается знак плюс или минус в зависимости от того, одинаково или противоположно направлены векторы
, где выбирается знак плюс или минус в зависимости от того, одинаково или противоположно направлены векторы 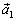 , и
, и 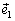 . Но,
. Но, 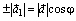 , где φ - угол между векторами
, где φ - угол между векторами 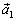 , и
, и 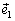 . Итак,
. Итак, 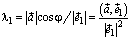 . Аналогично вычисляются и остальные компоненты.
. Аналогично вычисляются и остальные компоненты.
Скалярное произведение используется для решения следующих основных задач:
1.  ; 2.
; 2. 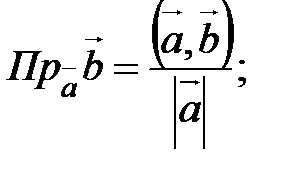 3.
3. 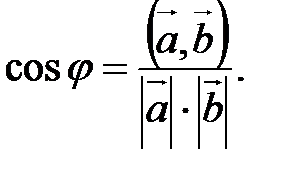
Пусть в некотором базисе 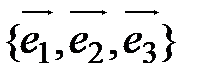 заданы векторы
заданы векторы 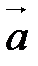 =
= 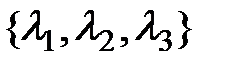 и
и 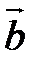 =
=  . Тогда, в ортонормированном базисе
. Тогда, в ортонормированном базисе
(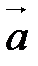 ,
, 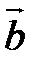 ) =
) = 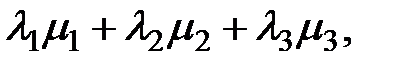
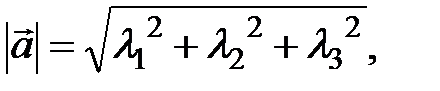
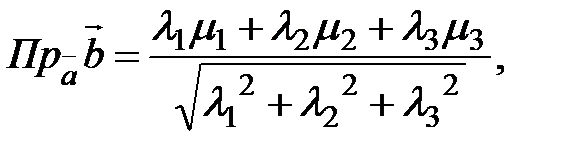
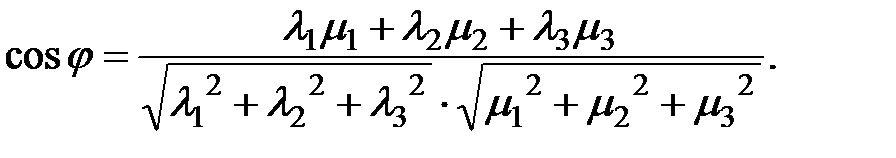
Не нашли, что искали? Воспользуйтесь поиском: