
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Смешанное произведение трех векторов. Выражение смешанного произведения через координаты перемножаемых векторов.
Число ( ,[
,[  ,
,  ]) называется смешанным произведением векторов
]) называется смешанным произведением векторов  ,
, 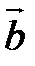 и
и  .
.
Смешанное произведение векторов  ,
,  и
и  обозначается (
обозначается ( ,
,  ,
,  ).
).
Теорема 5. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, взятому со знаком плюс если тройка правая, и со знаком минус, если тройка левая.
Действительно,  , где φ - угол между векторами
, где φ - угол между векторами 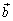 и
и  , а θ - угол между векторами
, а θ - угол между векторами 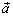 и
и  . Объем параллелепипеда, построенного на векторах
. Объем параллелепипеда, построенного на векторах 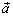 ,
, 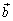 и
и  , равен (рис. 13) произведению площади основания
, равен (рис. 13) произведению площади основания  на высоту
на высоту  . Таким образом, первое утверждение доказано. Знак смешанного произведения совпадает со знаком cosθ, и поэтому смешанное произведение положительно когда
. Таким образом, первое утверждение доказано. Знак смешанного произведения совпадает со знаком cosθ, и поэтому смешанное произведение положительно когда 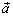 направлен в ту же сторону от плоскости векторов
направлен в ту же сторону от плоскости векторов 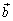 и
и  , что и вектор
, что и вектор  , т. е. когда тройка
, т. е. когда тройка 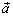 ,
, 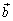 ,
,  правая. Аналогично доказывается, что смешанное произведение левой тройки векторов отрицательно.
правая. Аналогично доказывается, что смешанное произведение левой тройки векторов отрицательно.

Теорема 6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Равенство  возможно в следующих случаях:
возможно в следующих случаях:
a.хотя бы один вектор нулевой; тогда все три вектоpaкомпланарны;
b.sinφ = 0 тогда 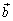 и
и  коллинеарны, и следовательно
коллинеарны, и следовательно 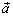 ,
, 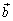 и
и  компланарны;
компланарны;
c.cosθ = 0 тогда вектор 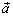 ортогонален
ортогонален  , т. е. компланарен
, т. е. компланарен 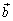 и
и  .
.
Обратное утверждение доказывается аналогично.
Смешанное произведение обладает следующими свойствами:
1. ( ,
,  ,
,  ) = (
) = ( ,
,  ,
,  ) = (
) = (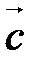 ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  );
);
2. ( ,
,  ,
,  ) = (
) = ( ,
,  ,
,  ) + (
) + ( ,
, 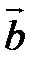 ,
,  );
);
3. (
 ,
,  ,
,  ) =
) =  (
( ,
,  ,
,  ).
).
Пусть в некотором базисе  векторы
векторы  =
=  ,
,  =
=  ,
,  =
= 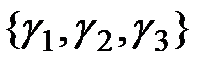 , тогда
, тогда
( ,
,  ,
,  ) =
) = 
В частности, в ортонормированном базисе
( ,
,  ,
,  ) =
) = 
(если базис левый, то перед одной из частей равенства следует поставить знак минус).
Следствие. Условие  является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе.
является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе.
Условие коллинеарности двух векторов. Условие компланарности трех векторов.
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Равенство  возможно в следующих случаях:
возможно в следующих случаях:
хотя бы один вектор нулевой; тогда все три вектоpaкомпланарны;
sinφ = 0 тогда 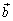 и
и  коллинеарны, и следовательно
коллинеарны, и следовательно 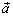 ,
, 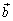 и
и  компланарны;
компланарны;
cosθ = 0 тогда вектор 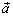 ортогонален
ортогонален  , т. е. компланарен
, т. е. компланарен 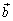 и
и  .
.
Обратное утверждение доказывается аналогично.
Смешанное произведение обладает следующими свойствами:
( ,
,  ,
,  ) = (
) = ( ,
,  ,
,  ) = (
) = (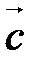 ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  ) = - (
) = - ( ,
,  ,
,  );
);
( ,
,  ,
,  ) = (
) = ( ,
,  ,
,  ) + (
) + ( ,
, 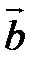 ,
,  );
);
(
 ,
,  ,
,  ) =
) =  (
( ,
,  ,
,  ).
).
Пусть в некотором базисе  векторы
векторы  =
=  ,
,  =
=  ,
,  =
= 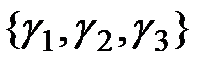 , тогда
, тогда
( ,
,  ,
,  ) =
) = 
В частности, в ортонормированном базисе
( ,
,  ,
,  ) =
) = 
(если базис левый, то перед одной из частей равенства следует поставить знак минус).
Следствие. Условие  является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе.
является необходимым и достаточным условием компланарности трех векторов, заданных своими координатами в некотором базисе.
Не нашли, что искали? Воспользуйтесь поиском: