
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Векторное произведение двух векторов. Выражение векторного произведения через координаты перемножаемых векторов.
Векторным произведением вектора 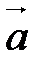 на вектор
на вектор  называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1.  где φ – угол между векторами
где φ – угол между векторами  и
и  ;
;
2. вектор 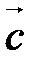 ортогонален вектору
ортогонален вектору  , вектор
, вектор  ортогонален вектору
ортогонален вектору  ;
;
3. упорядоченная тройка векторов { 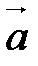 ,
, 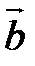 ,
,  } является правой.
} является правой.
Замечание. Если один из векторов нулевой, то векторное произведение есть нулевой вектор.
Векторное произведение вектора  на вектор
на вектор  обозначается [
обозначается [  ,
,  ].
].
Теорема 2. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Теорема 3. Длина (модуль) векторного произведения двух векторов равняется площади параллелограмма, построенного на этих векторах как на сторонах.
Действительно, можно заметить, что 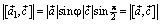 . Вектор
. Вектор 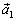 компланарен векторам
компланарен векторам 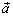 и
и  , а потому
, а потому  и
и  коллинеарны. Легко видеть (рис. 12), что они одинаково направлены.
коллинеарны. Легко видеть (рис. 12), что они одинаково направлены.
Векторное произведение обладает следующими свойствами:
1. [  ,
,  ] = - [
] = - [  ,
,  ] (антикоммутативность);
] (антикоммутативность);
Действительно, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей. Точно так же вектор 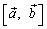 коллинеарен вектору
коллинеарен вектору 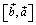 . Однако, переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если
. Однако, переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если 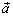 ,
, 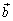 ,
, 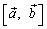 - правая тройка, то
- правая тройка, то 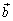 ,
, 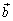 ,
, 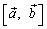 - левая, а
- левая, а 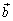 ,
, 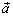 ,
,  - снова правая тройка.
- снова правая тройка.
2. [ 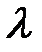
 ,
,  ] =
] =  [
[  ,
,  ];
];
Если φ - угол между векторами 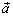 и
и 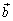 , то
, то  . Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной
. Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной 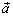 и
и 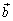 . При λ > 0 и вектор
. При λ > 0 и вектор  и
и 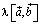 вектор направлены так же, как
вектор направлены так же, как 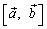 . Если λ < 0, то кратчайший поворот от
. Если λ < 0, то кратчайший поворот от 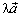 к
к 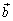 производится навстречу кратчайшему повороту от
производится навстречу кратчайшему повороту от 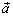 к
к 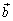 . Поэтому
. Поэтому 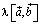 и
и 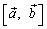 противоположно направлены. Очевидно, что противоположно направлены также и векторы
противоположно направлены. Очевидно, что противоположно направлены также и векторы  и
и 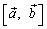 . Таким образом, при λ ≠ 0 векторы
. Таким образом, при λ ≠ 0 векторы  и
и 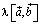 направлены всегда одинаково, и равенство доказано. При λ = 0 равенство очевидно.
направлены всегда одинаково, и равенство доказано. При λ = 0 равенство очевидно.
3. [  +
+  ,
,  ] = [
] = [  ,
,  ] + [
] + [  ,
,  ];
];
Если  , то доказываемое очевидно. Если
, то доказываемое очевидно. Если 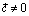 , то разложим
, то разложим 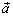 и
и 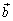 в суммы
в суммы  и
и  , где
, где 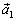 и
и  ортогональны
ортогональны  , а
, а 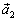 и
и  коллинеарны
коллинеарны  . Поскольку
. Поскольку 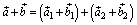 , и вектор
, и вектор  ортогонален
ортогонален  , а
, а  коллинеарен
коллинеарен  , нам достаточно доказать равенство
, нам достаточно доказать равенство  и (в силу свойства 2) даже равенство
и (в силу свойства 2) даже равенство  , где
, где 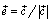 . Длина вектора
. Длина вектора 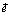 равна 1. Выше, в примере, мы видели, что в этом случае умножение на
равна 1. Выше, в примере, мы видели, что в этом случае умножение на 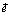 сводится к повороту (ортогонального к
сводится к повороту (ортогонального к 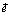 ) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на
) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на 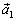 и
и  , поворачивается целиком вместе с диагональю. Тем самым равенство доказано.
, поворачивается целиком вместе с диагональю. Тем самым равенство доказано.
4. [  ,
, 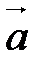 ] = 0.
] = 0.
Пусть в некотором базисе  заданы векторы
заданы векторы  =
=  и
и 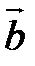 =
= 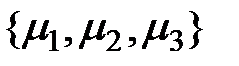 тогда
тогда
[  ,
, 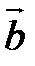 ] =
] = 
Теорема 4. В ортонормированном базисе [  ,
,  ] =
] =  (если базис левый, то перед одной из частей равенства следует поставить знак минус).
(если базис левый, то перед одной из частей равенства следует поставить знак минус).
Справедливость теоремы следует из предыдущих формул при учете примеров в начале раздела. Чтобы избежать постоянных замечаний об ориентации базиса, мы будем считать, что базис выбирается всегда правый.
Векторное произведение используется в основном для решения двух задач:
1. Нахождения вектора перпендикулярного плоскости, в которой расположены два заданных вектора.
2. Вычисление площади S параллелограмма, построенного на векторах  и
и  , как на сторонах. В ортонормированном базисе
, как на сторонах. В ортонормированном базисе

Не нашли, что искали? Воспользуйтесь поиском: