Общее уравнение прямой. Неполные уравнения прямой. Уравнение прямой в отрезках.

Общее уравнение прямой на плоскости. Рассмотрим на плоскости Оху произвольную прямую L. Пусть дана некоторая ее точка М1(х1у1) и вектор N=Ai+Bj, перпендикулярный рассматриваемой прямой. Этот вектор называется нормальным вектором прямой. Точка М1 и нормальный вектор N вполне определяют положение прямой L на плоскости Оху. Пусть М(х,у) - любая точка прямой L. По условию, вектор N перпендикулярен вектору , лежащему на этой прямой. Поэтому скалярное произведение (N, )=0, или в координатной форме А(х–х1)+В(у–у1)=0. Раскроем скобки: Ах+Ву+(-Ах1–Ву1)=0.

В скобках получаем некоторое число, так как А и В числовые коэффициенты, а х1 и у1 - координаты точки и, если это число обозначим С, то получится общее уравнение прямой на плоскости:

Ах + Ву + С = 0.

Каноническое уравнение. Далее, положение прямой L на плоскости вполне определяется заданием какой-либо ее точки М(х1,у1) и вектора S=mi+nj, параллельного L или лежащего на ней. Этот вектор называется направляющим вектором прямой L. Пусть М(х,у) - произвольная точка прямой L. Так как векторы 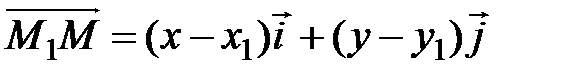и S=mi+nj коллинеарны (по условию), то их координаты пропорциональны. Следовательно, каноническое уравнение прямой имеет вид

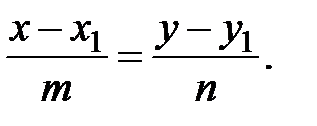
Параметрическое уравнение прямой на плоскости:

или

Здесь Aо = (хо, уо) – некоторая точка на прямой (начальная), а = (α,β) – некоторый ненулевой вектор (направляющий). Выражая t, получаем каноническое уравнение прямой.

Не нашли, что искали? Воспользуйтесь поиском: