Непрерывность функции. Виды разрывов функции.

Определение. Функция f(x) называется непрерывной в точке 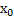, если в этой точке выполняется соотношение 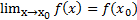, то есть предел функции равен значению функции в точке . У непрерывной функции знак предела и знак функции можно поменять местами.

Функция непрерывна в точке, если:

1) она определена в точке

2) есть ее предел в точке

3) предел функции в точке равен ее значению в т.

Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть

Функция f(x) называется непрерывной в т. 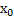справа, если ;

Функция f(x) называется непрерывной в т. 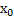слева, если ;

Таким образом, функция f(x) непрерывна в т. 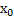, если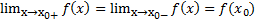

Непрерывность - это свойство, которым обладает каждая из элементарных функций во всякой точке, где она определена.

Разрывная функция - функция, не являющаяся непрерывной хотя бы в одной точке области определения.

Виды разрывов:

устранение разрыва - функция в точке не определена, но есть ее предел в точке.

1) разрыв 1-го рода (имеет место тогда, когда предела функции нет, но есть оба односторонних предела. Чтобы устранить его, нужно доопределить функцию в т. 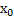или переопределить.

Абсолютная величина разности между односторонними пределами называется скачком функции в точке разрыва.

2) разрыв 2-го рода (имеет место тогда, когда хотя бы один из односторонних пределов не существует или равен 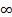). Разрыв 2-го рода всегда неустраним.

Не нашли, что искали? Воспользуйтесь поиском: