Предел функции в точке. Предел функции на бесконечности.

Предел функции в точке (при х→ )

Пусть f(x) определена на множестве Х и пусть точка 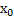такова, что или 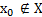. Построим числовую последовательность, сходящуюся к :

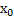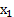, , …, (6.3)

Вычисленные в этих точках значения функции также образуют числовую последовательность:

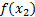, , …, .(6.4)

Поставим вопрос о пределе последовательности (6.4).

Определение. Число А называется пределом функции в точке 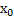, если для любого сколь угодно малого числа Е(эпсилон) > 0 существует такое число δ (дельта) > 0, что для всех удовлетворяющих условию |x – 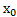| < δ выполняется неравенство |f(x) – A| < Е (6.5)

ИЛИ такое определение: Число А является пределом функции F(x) в точке А, если для любого сколь угодно малого числа Е > 0, существует такое положительное число δ (Дельта), зависящее от Е, что для всех точек Х из дельта окрестности т. А удовлетворяющим неравенству |x –а| < δ выполняется неравенство |f(x) – A| < Е

Обозначают:

Предел функции на бесконечности

Этот предел позволяет определить как выглядит график функции при или

Определение. В названном пределом функции y = f(x) при , если для любого сколь угодно малого Е > 0 найдется такое число М>0, чтобы для любых Х удовлетворяющих неравенству │х│> М выполняется │f(x) - B│< E

Обозначают: ,

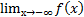
Не нашли, что искали? Воспользуйтесь поиском: